Quantum Error Correction and the Floquet Codes

Julien Bréhier

University of Bonn March 14, 2025

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

Important notions

  • Stabilizer codes
  • Distance of a code
  • 'Good codes'
  • Logical operators
  • Minimum Weight Perfect Matching
  • Ancilla measurements
  • Error Correcting
  • Fault tolerance
  • Transversal operators
  • Lattice Surgery

Stabilizer codes

Stabilizer codes

\text {For a stabilizer code }\llbracket n,k,d \rrbracket

Stabilizer codes

\text {For a stabilizer code }\llbracket n,k,d \rrbracket
\set{\forall s_i,s_j \in \mathcal{S} \subsetneq\mathcal{P}^n,[s_i,s_j]=0}

Stabilizer codes

\text {For a stabilizer code }\llbracket n,k,d \rrbracket
\forall s \in \mathcal{S},s\bar{\ket{\psi}} = {\color{red}+} \bar{\ket{\psi}}
\set{\forall s_i,s_j \in \mathcal{S} \subsetneq\mathcal{P}^n,[s_i,s_j]=0}

Stabilizer codes

\text {For a stabilizer code }\llbracket n,k,d \rrbracket
\forall s \in \mathcal{S},s\bar{\ket{\psi}} = {\color{red}+} \bar{\ket{\psi}}
k = n-rank(\mathcal{S})
\set{\forall s_i,s_j \in \mathcal{S} \subsetneq\mathcal{P}^n,[s_i,s_j]=0}

The 3-Qubit Code

The 3-Qubit Code

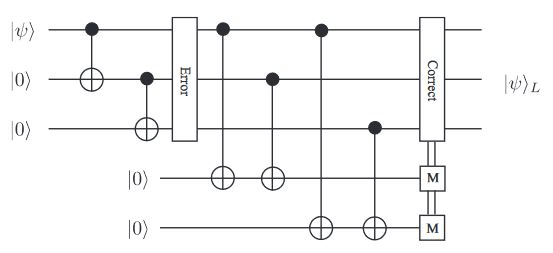
https://arxiv.org/pdf/0905.2794

The 3-Qubit Code

https://arxiv.org/pdf/0905.2794

s = \langle Z_1Z_2,Z_1Z_3\rangle

The 3-Qubit Code

https://arxiv.org/pdf/0905.2794

s = \langle Z_1Z_2,Z_1Z_3\rangle
|\bar{0}\rangle = |000\rangle \\ |\bar{1}\rangle = |111\rangle

The Steane Code

https://arthurpesah.me/blog/2023-03-16-stabilizer-formalism-2/

The Steane Code

\begin{align*} & IIIXXXX \\ & IXXIIXX \\ & XIXIXIX \\ & IIIZZZZ \\ & IZZIIZZ \\ & ZIZIZIZ \end{align*}

https://arthurpesah.me/blog/2023-03-16-stabilizer-formalism-2/

The Steane Code

\begin{align*} \bar{X} & = XXXXXXX \\ \bar{Z} & = ZZZZZZZ. \end{align*}

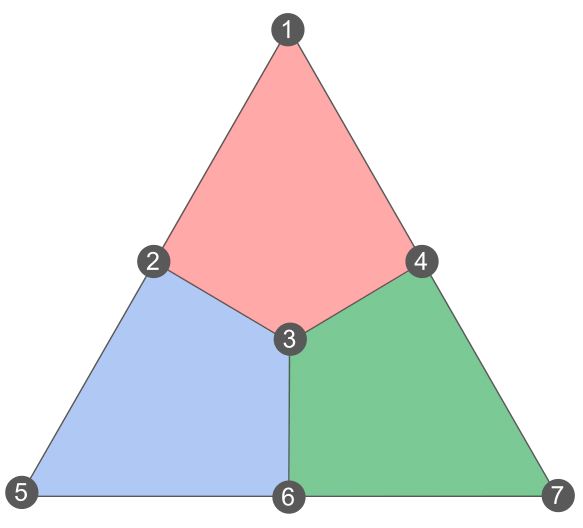
https://arthurpesah.me/blog/2023-03-16-stabilizer-formalism-2/

The Search for Good Codes

The Search for Good Codes

You might remember :

The Search for Good Codes

` \text {For a stabilizer code }\llbracket n,k,d \rrbracket ,

You might remember :

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

Hamiltonian

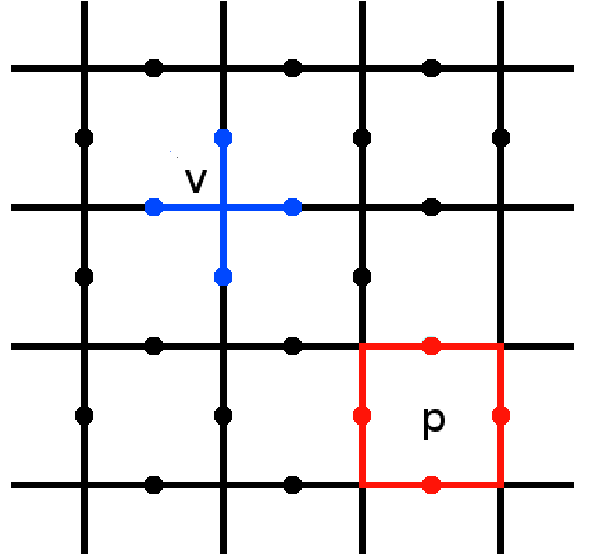
A_v = \prod_{i \in v} \sigma^x_i, \,\,\\ B_p = \prod_{i \in p} \sigma^z_i

Logical Operators

https://errorcorrectionzoo.org/c/toric

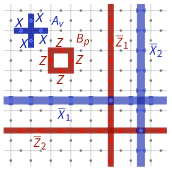
Minimum Weight Perfect Matching

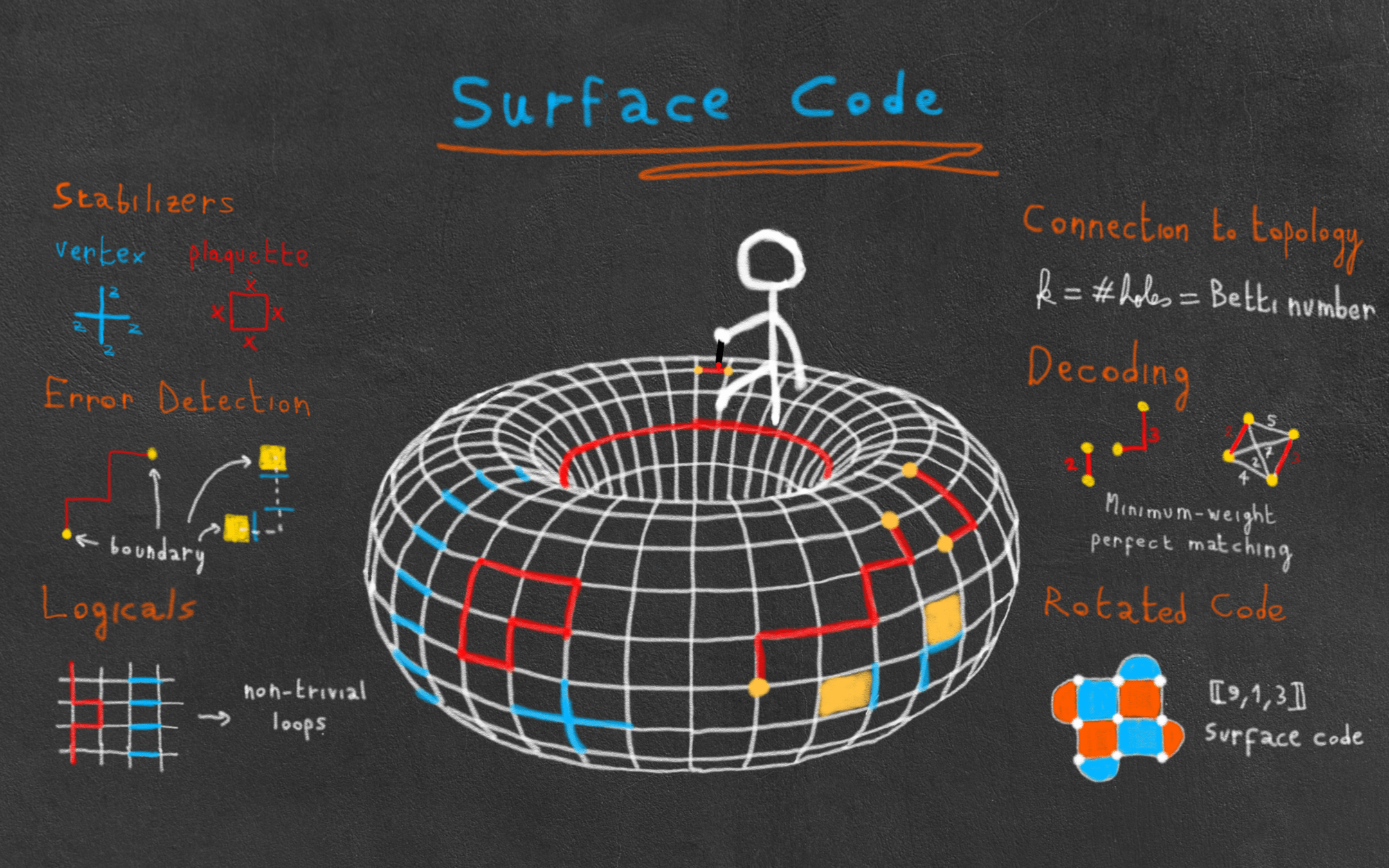
https://arthurpesah.me/blog/2023-05-13-surface-code/

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

Measurement Method Through Ancilla

Other Measurements

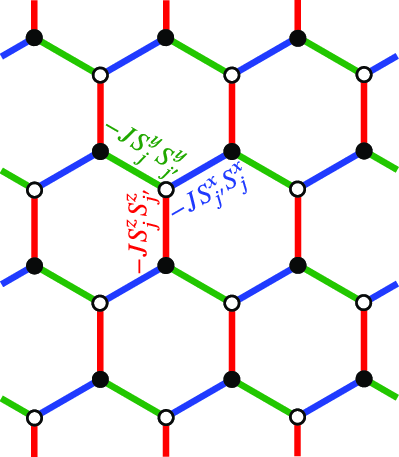
Kitaev Spin Model

THC Yields No Qubit

e = 3p
q = 2p
s = (p - 1) + 2 = p + 1
|\mathcal{G}| = 3p - 1
g = \frac{|\mathcal{G}| - |\mathcal{S}|}{2} = \frac{3p - 1 - (p + 1)}{2} = p - 1
k + g + s = n \quad \Longleftrightarrow \quad k + (p - 1) + (p + 1) = 2p

Floquet-ness

Toric Code ?

Two Protected Operators

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

Setting boundaries

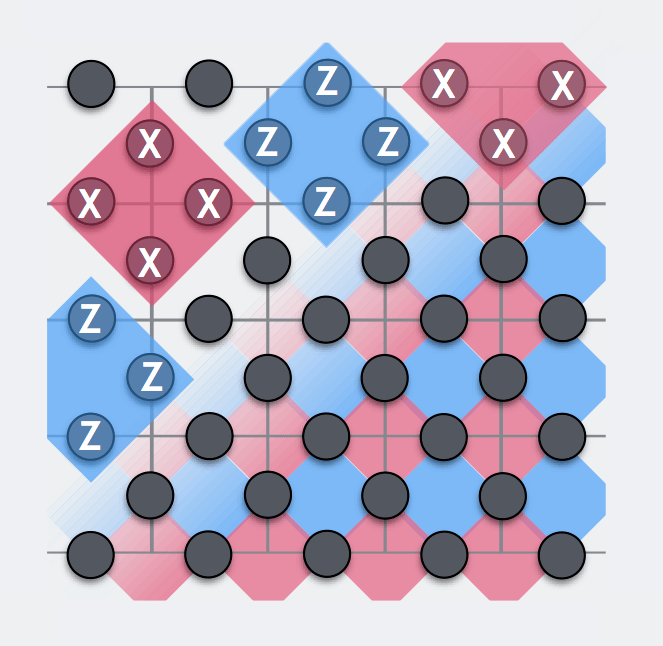
https://quantumcomputing.stackexchange.com/questions/4395/how-is-computation-done-in-a-2d-surface-code-array

The Surface Code

The Planar Honeycomb Floquet Code (PHFC)

Careful with the edges

Notion of threshold

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

Idea of Fault Tolerance

The Steane Code

\begin{align*} & IIIXXXX \\ & IXXIIXX \\ & XIXIXIX \\ & IIIZZZZ \\ & IZZIIZZ \\ & ZIZIZIZ \end{align*}
\bar{U} = U^{\otimes n}

The Steane Code

\begin{align*} & IIIXXXX \\ & IXXIIXX \\ & XIXIXIX \\ & IIIZZZZ \\ & IZZIIZZ \\ & ZIZIZIZ \end{align*}
\begin{align*} \bar{X} & = XXXXXXX \\ \bar{Z} & = ZZZZZZZ. \end{align*}
\bar{U} = U^{\otimes n}

Surface Code Example

S = \sqrt{Z}

Surface Code Example

S = \sqrt{Z}
\bar{S} = S^{\otimes 9}

PHFC Example

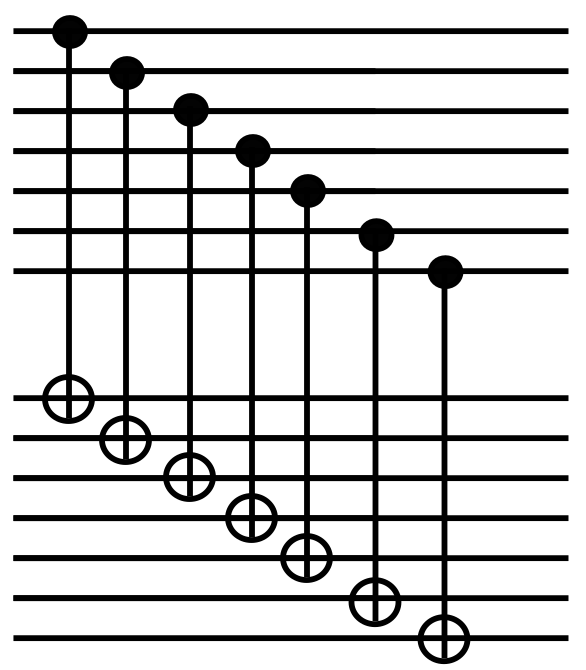
https://quantumcomputing.stackexchange.com/questions/24269/what-is-formally-a-transversal-operator

PHFC Example

https://quantumcomputing.stackexchange.com/questions/24269/what-is-formally-a-transversal-operator

PHFC Example

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

What is it ?

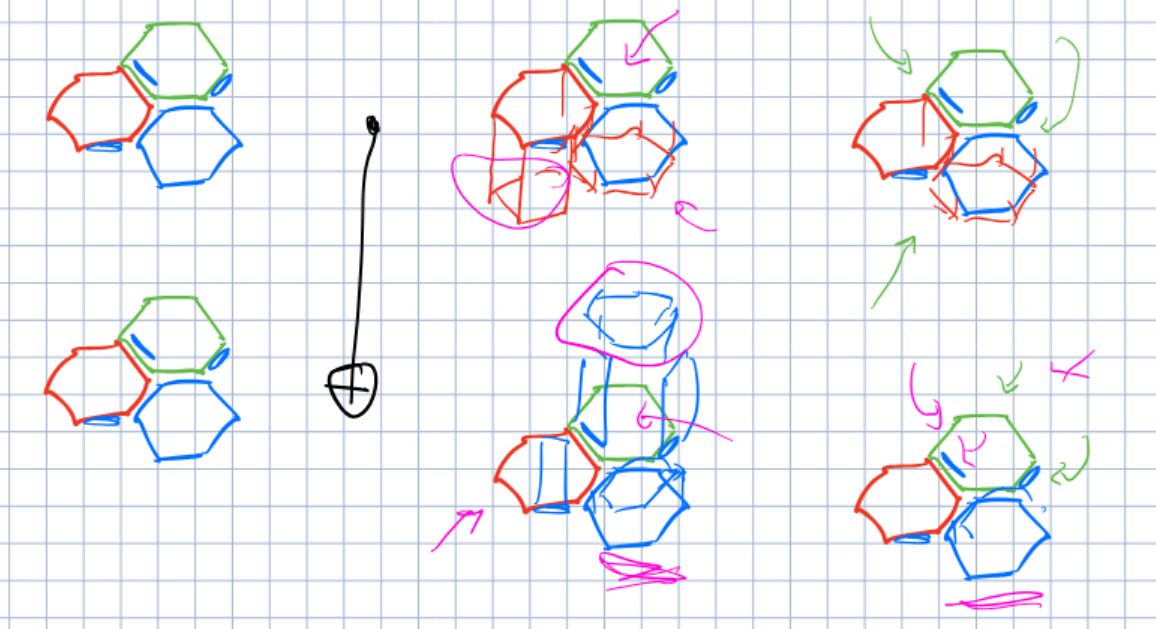
CNot gate

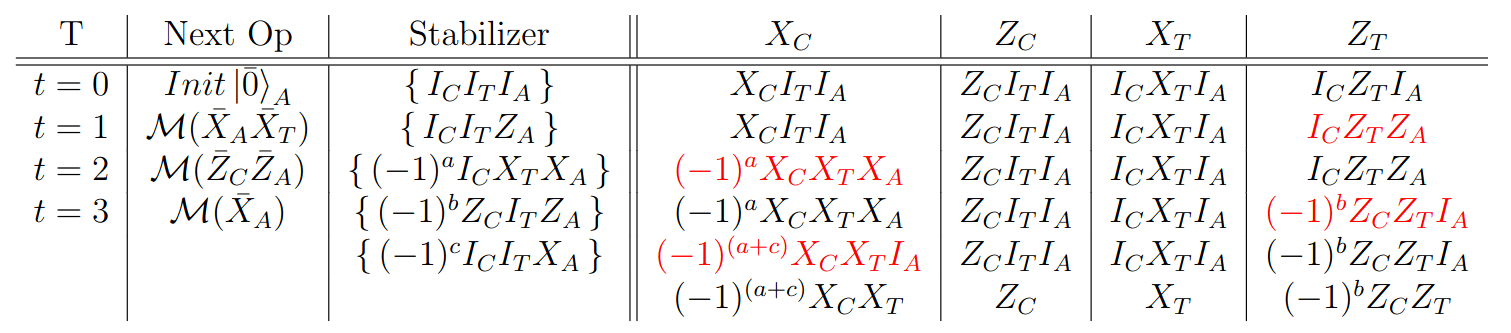
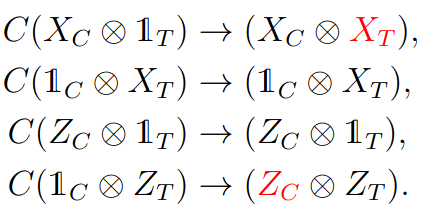
CNot gate

Init\ket{\bar{0}}_A \xrightarrow{} \mathcal{M} (\bar{X}_A\bar{X}_T)\\ \xrightarrow{} \mathcal{M}(\bar{Z}_C\bar{Z}_A)\xrightarrow{} \mathcal{M}(\bar{X}_A)
Init\ket{\bar{+}}_A \xrightarrow{} \mathcal{M}(\bar{Z}_C\bar{Z}_A) \\ \xrightarrow{} \mathcal{M} (\bar{X}_A\bar{X}_T)\xrightarrow{} \mathcal{M}(\bar{Z}_A)

Space time diagram

Journey Through Quantum Error Correction

  • Introduction
  • The Toric Code
  • The Toric Honeycomb Floquet Code (THFC)
  • Cutting Slices
  • Transversal Operators
  • Lattice Surgery (LS)
  • Prospects

Important notions

  • Stabilizer codes
  • Distance of a code
  • 'Good codes'
  • Logical operators
  • Minimum Weight Perfect Matching
  • Ancilla measurements
  • Error Correcting
  • Fault tolerance
  • Transversal operators
  • Lattice Surgery

Future ideas

  • Publish the results comparing the two techniques
  • Compare different implementations of the planar codes
  • Test experimentally

Quantum Error Correction and the Floquet Codes

By Julien Bréhier

Made with Slides.com

Quantum Error Correction and the Floquet Codes

  • 1

More from Julien Bréhier