Logical Entanglement via LS
Good qLDPC codes
Excerpt from Wikipedia
Good
'dqLDPC' codes ?
Standard depolarising noise
Entangling Measurements
First version :
Toric HFC
Just like the Toric Code
The Planar Honeycomb Floquet Codes
Setting boundaries
An error corrected Planar HFC
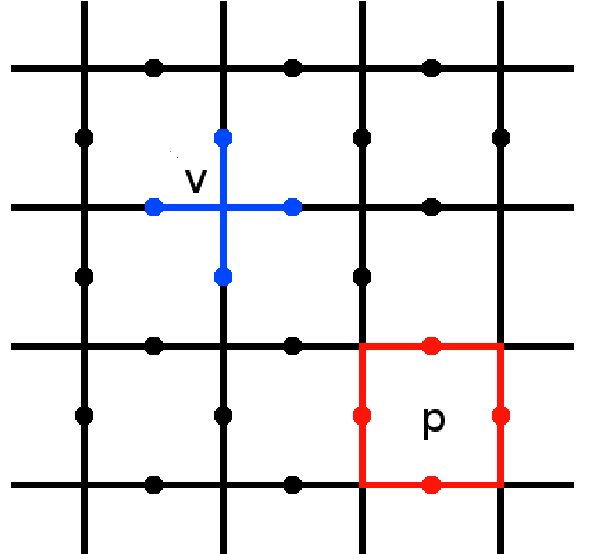
Naming the operators
Naming the operators
Lattice surgery
Lattice surgery
Lattice surgery on the PHFC
With error correction
With error correction
CNot gate
Init\ket{\bar{0}}_A \xrightarrow{} \mathcal{M} (\bar{X}_A\bar{X}_T)\\
\xrightarrow{} \mathcal{M}(\bar{Z}_C\bar{Z}_A)\xrightarrow{} \mathcal{M}(\bar{X}_A)
CNot gate
Init\ket{\bar{0}}_A \xrightarrow{} \mathcal{M} (\bar{X}_A\bar{X}_T)\\
\xrightarrow{} \mathcal{M}(\bar{Z}_C\bar{Z}_A)\xrightarrow{} \mathcal{M}(\bar{X}_A)
Init\ket{\bar{+}}_A \xrightarrow{} \mathcal{M}(\bar{Z}_C\bar{Z}_A) \\
\xrightarrow{} \mathcal{M} (\bar{X}_A\bar{X}_T)\xrightarrow{} \mathcal{M}(\bar{Z}_A)
CNot gate
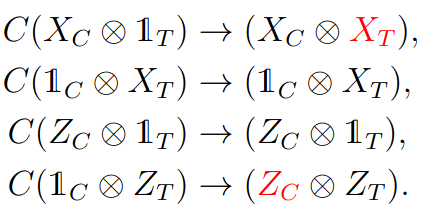
CNot gate
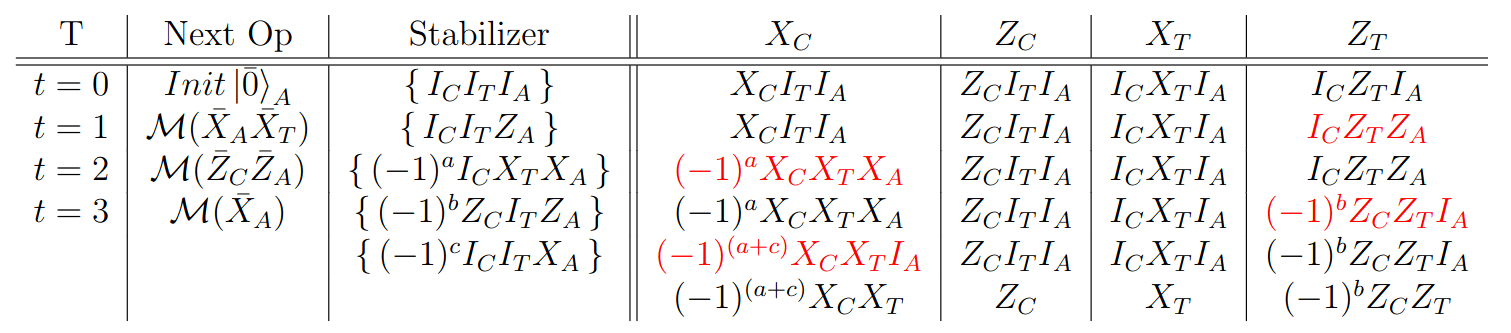
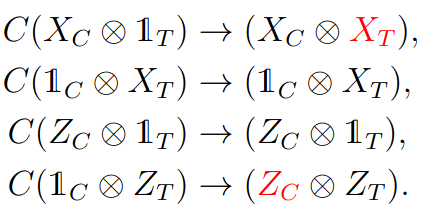
C
T
A
\text{CNot}_{C,T}
C
T
A
X_TX_A
C
T
A
Z_CZ_A
C
T
A
X_A
C
T
A
\text{Result}
Scalability
-
Init
- Entertain 3*d rounds
- XX
- Entertain 3*d rounds
- Split
- Entertain 3*d rounds
- ZZ
- Entertain 3*d rounds
- Split
- Entertain 3*d rounds
- Measure logical ancilla
- Entertain 3*d rounds
- Measure logical data
Scalability
-
Init
- Entertain 3*d rounds
- XX
- Entertain 3*d rounds
- Split
- ZZ
- Entertain 3*d rounds
- Split
- Measure logical ancilla
- Entertain 3*d rounds
- Measure logical data
5700 -> 3800
Current
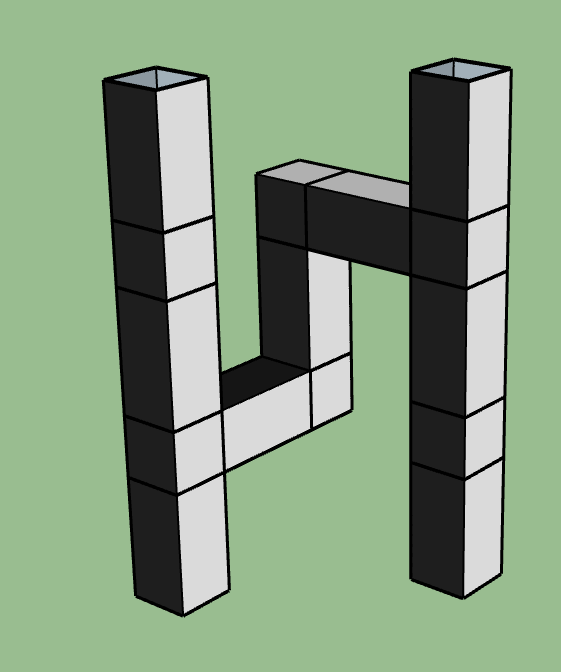
Easy to get
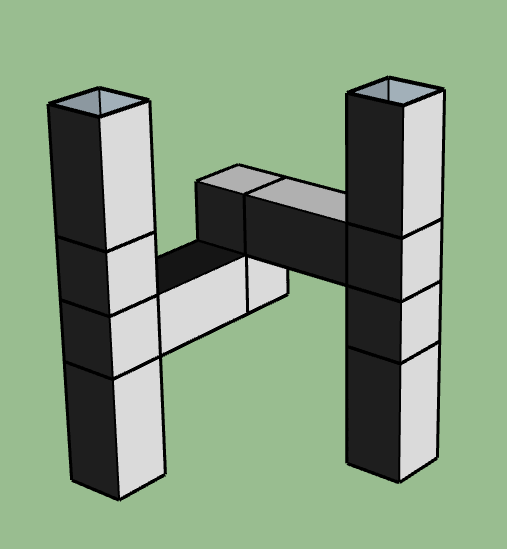
\text{CNot}_{C,T}
C
T
A
X_TX_A
C
T
A
Z_CZ_T
C
T
A
X_C
C
T
A
X_C
C
T
A
Harder
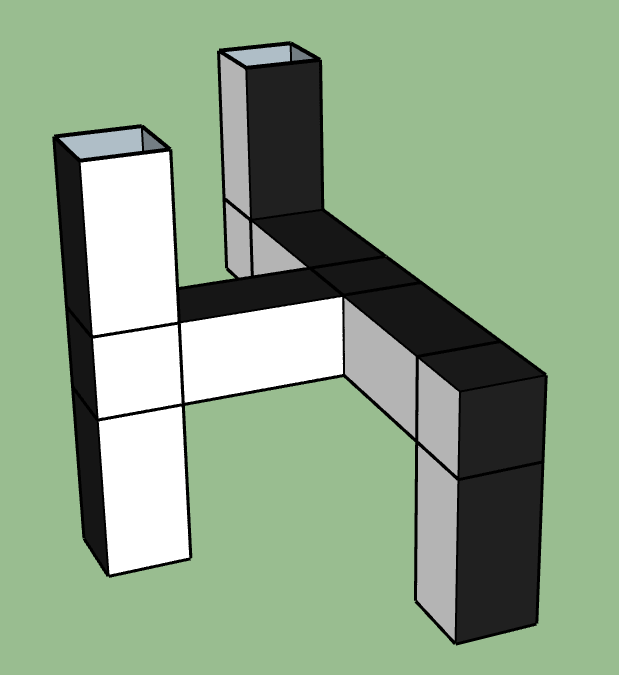
Copy of Copy of Group meeting
By Julien Bréhier
