Group meeting 11.03.25
Holidays in India



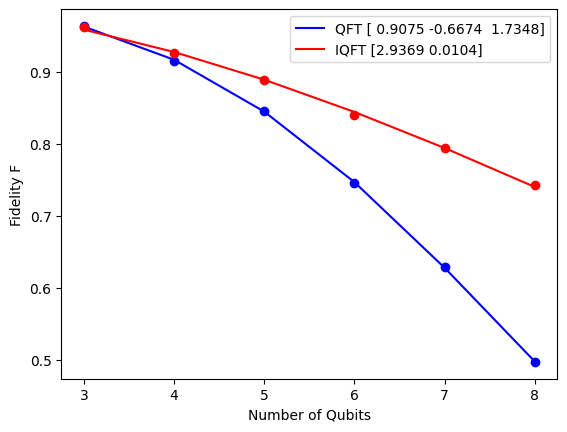
Noise characterization of QFT schemes
Short recall on the QFT
The family of gates
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
The family of gates
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & e^{i\theta}
\end{bmatrix}
The family of gates
The family of gates
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
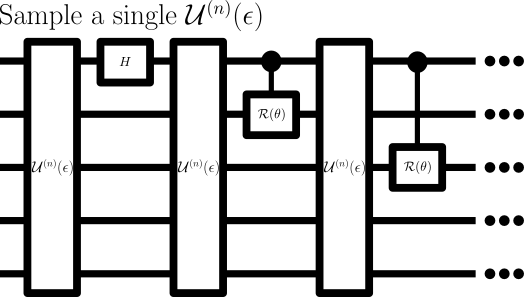
Scheme for the full algorithm
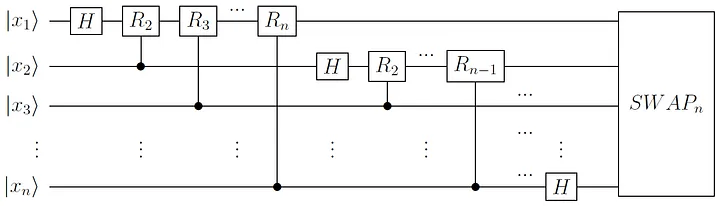
Scheme for the full algorithm

\text{Total of }n + n(n-1)/2 +\lfloor n/2\rfloor \propto n^2
Improving the resilience to unitary noise
Prosen et al. (2001)

The initial idea
\text{Theoretical limit of }\chi = \sum_{t,t'} C(t,t') \propto n^2
U_\delta = Ue^{-i\delta V}
The initial idea
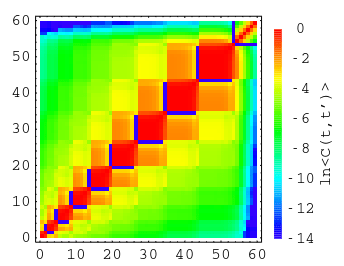
The initial idea

\chi \propto n^3
Replacing the 'bad gate'
[R_{jk},C_{\phi(jk)}]=0
R_{jk}^\dagger R_{jk}=1
\text{Tr}(R_{jk})=0
\begin{bmatrix}
0 & 0 & -1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & -1
\end{bmatrix}
Replacing
C_{\phi(01)}C_{\phi(02)}C_{\phi(03)}
R_{01}R_{02}R_{03}R_{01}^\dagger C_{\phi(01)}R_{02}^\dagger C_{\phi(02)}R_{03}^\dagger C_{\phi(03)}
Replacing
C_{\phi(01)}C_{\phi(02)}C_{\phi(03)}
R_{01}R_{02}R_{03}G_{01}G_{02}G_{03}
Death of the correlations
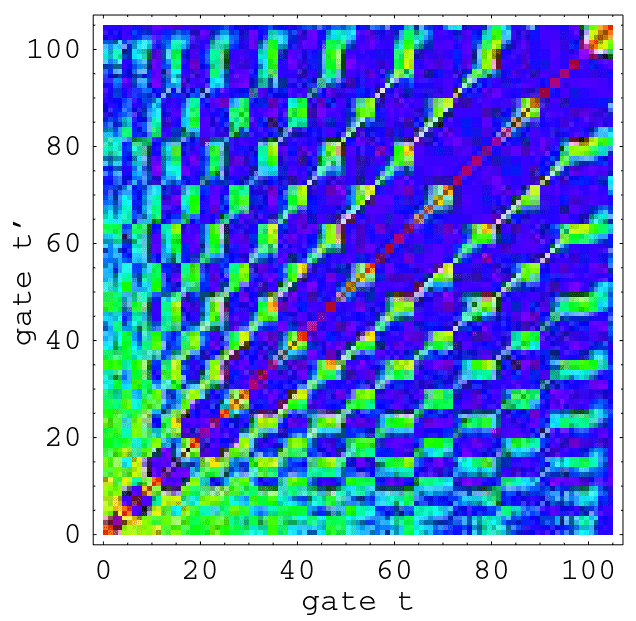
Suppression of the cubic term
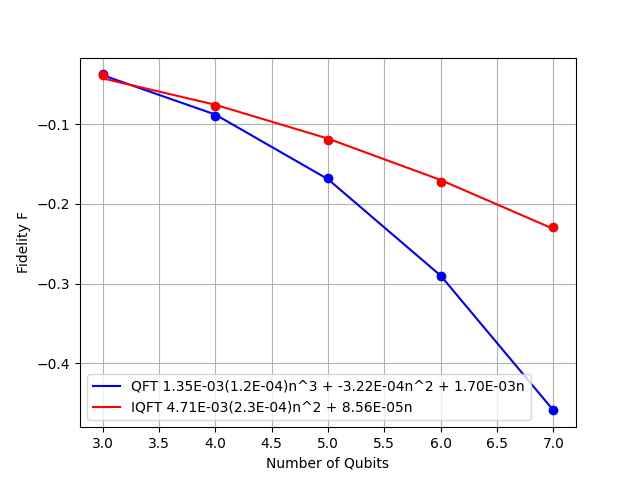
3 different avenues
3 different avenues
- Transition between regimes with dissipative noise
Kraus noise
\mathcal{E}(\rho) = \sum_i K_i \rho K_i^{\dagger}
\sum_i K_i^{\dagger} K_i = I
Which algorithm to chose
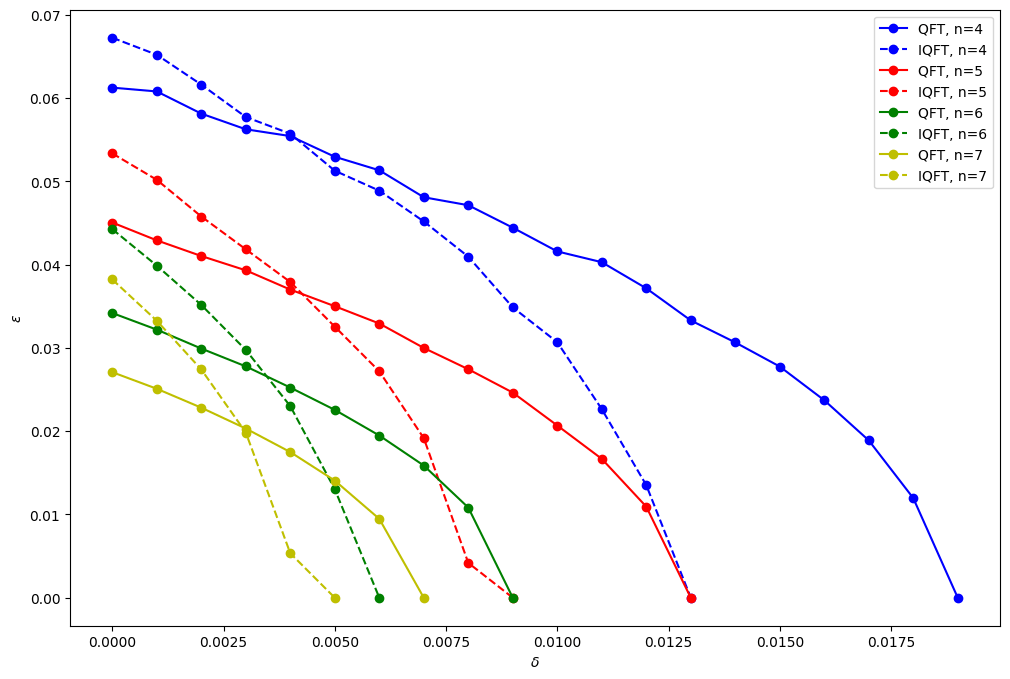
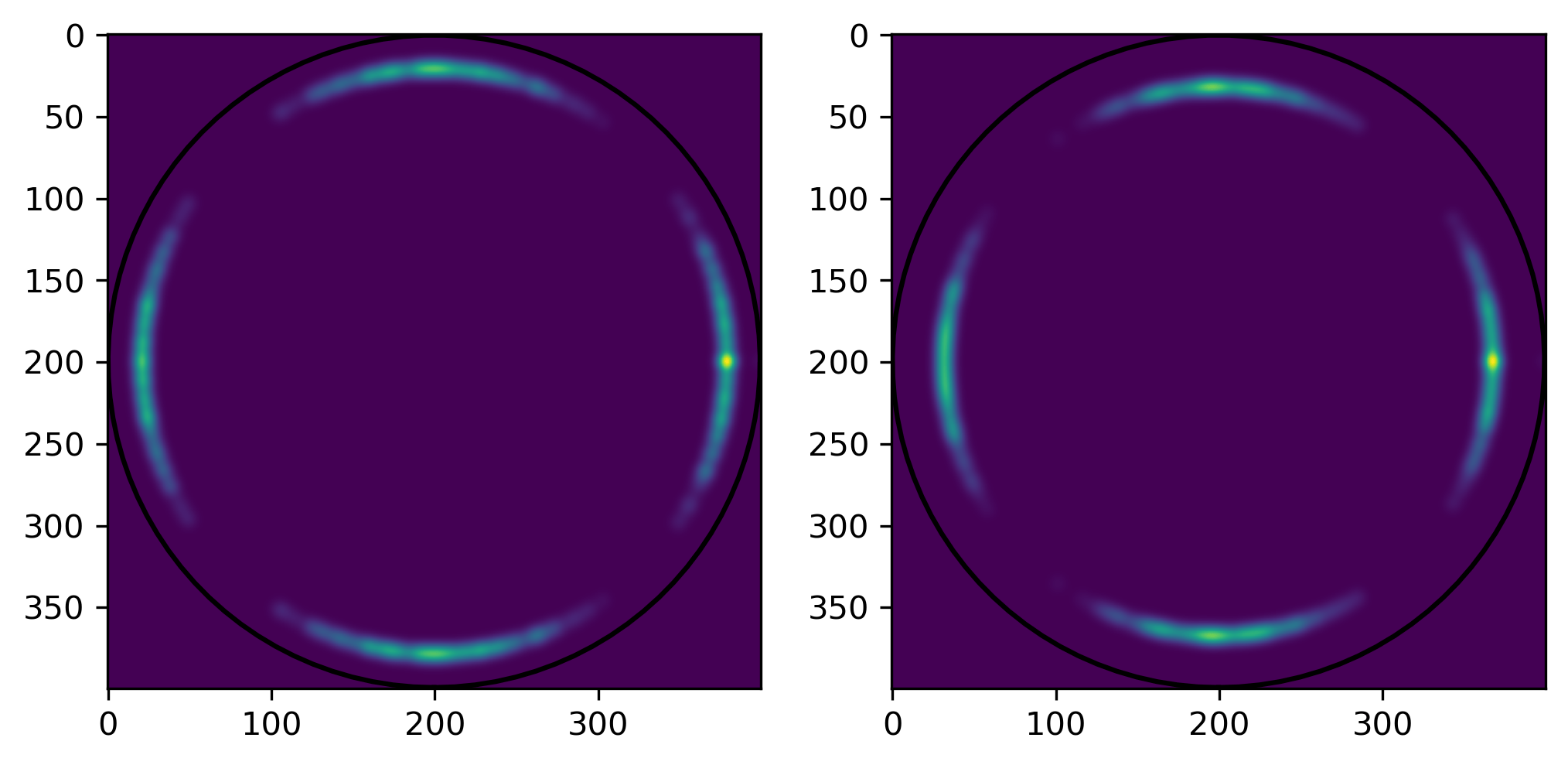
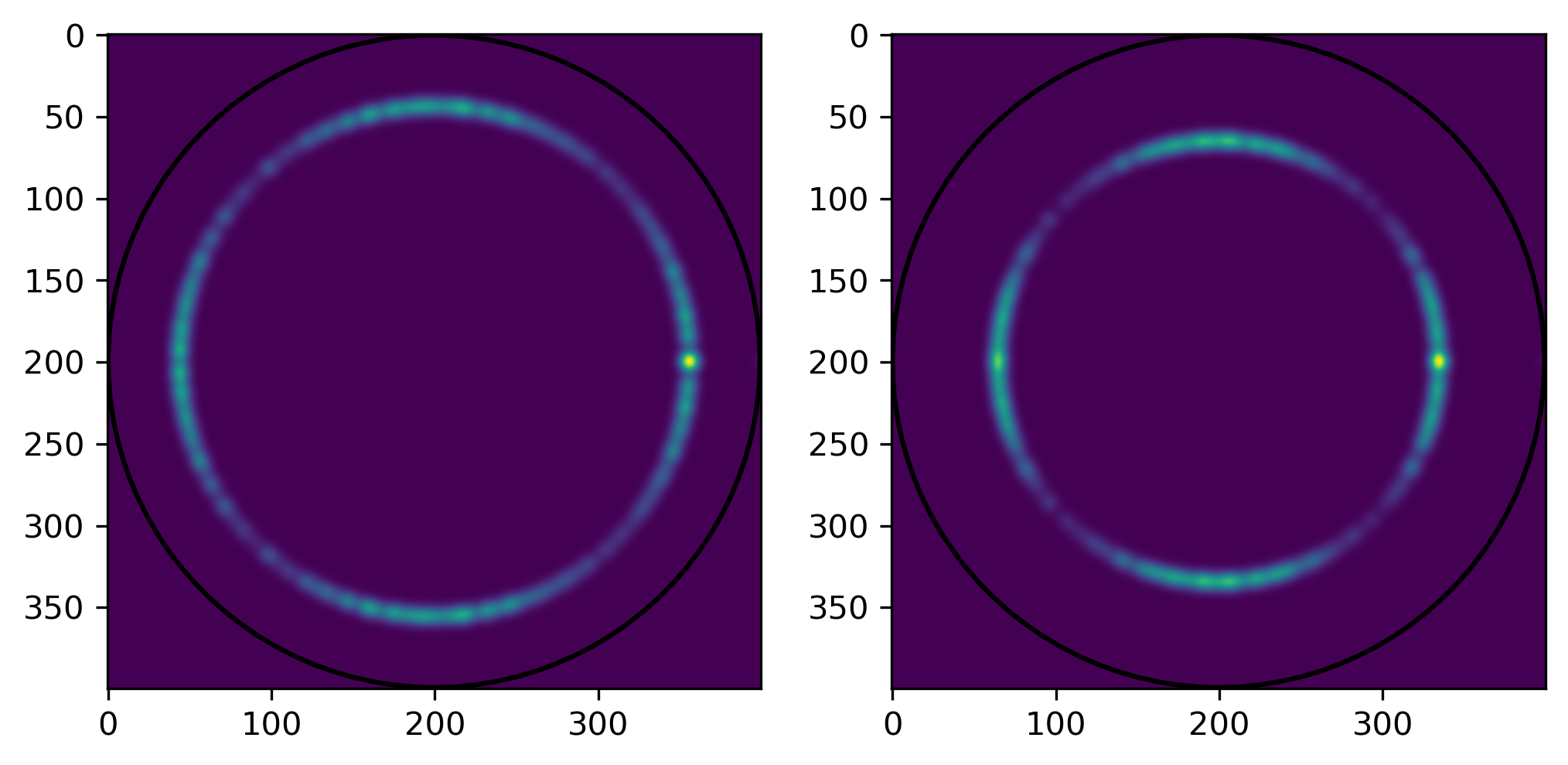
3 different avenues
- Transition between regimes with dissipative noise
- What other noise models show a cubic term we would benefit to suppress ?
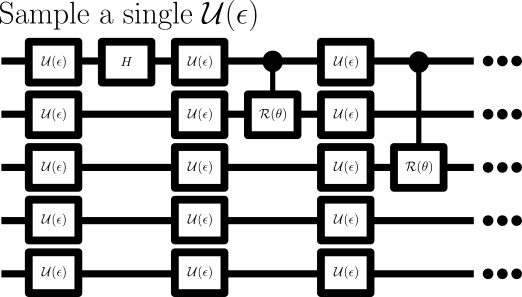
Original model
Other models
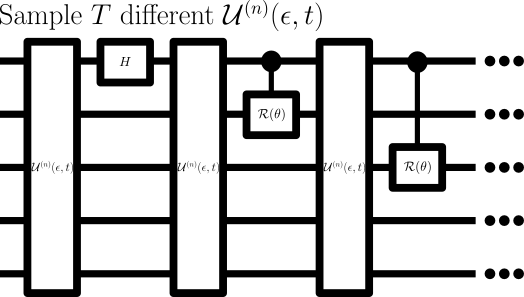
Original model

\sim
\sim
\sim
A model that works
Local one body
3 different avenues
- Transition between regimes with dissipative noise
- What other noise models show a cubic term we would benefit to suppress ?
- What more can we learn about the Kraus noise ?
Kraus noise
\mathcal{F}\sim \frac{f(\epsilon)}{2^L} - \delta T \left(1-\frac{1}{2^L}\right)
- First order dependency
- Rank independence of the first two moments of the fidelity
What to do next :
- Refine the contour plots and push the size slightly (11-12 qubits max)
- Investigate the 'approximately identical noise' models
- Find a good way to look at the spectra analysis
- Get further in terms of analytical results for the Kraus noise
What to do next :
- Refine the contour plots and push the size slightly (11-12 qubits max)
- Investigate the 'approximately identical noise' models
- Find a good way to look at the spectra analysis
- Get further in terms of analytical results for the Kraus noise
Thank you for your time !
iQFT
By Julien Bréhier
iQFT
- 1



