Mecanismos, grados de libertad, espacios de configuración y tarea
MT3005 - Robótica 1
De cuerpos rígidos a robots
\{A\}
\{B\}
(x_A,y_A,z_A,\phi_A,\theta_A,\psi_A)
(x_B,y_B,z_B,\phi_B,\theta_B,\psi_B)
6 parámetros (como mínimo) por cuerpo rígido
\{A\}
\{B\}
(x_A,y_A,z_A,\phi_A,\theta_A,\psi_A)
(x_B,y_B,z_B,\phi_B,\theta_B,\psi_B)
6 parámetros (como mínimo) por cuerpo rígido
problema
\{A\}
\{B\}
(x_A,y_A,z_A,\phi_A,\theta_A,\psi_A)
(x_B,y_B,z_B,\phi_B,\theta_B,\psi_B)
6 parámetros (como mínimo) por cuerpo rígido
problema
¿Solución?
q_1
q_2
sólo 2 parámetros!
restricciones juntas (joints)
eslabones (links)
q_1
q_2
restricciones juntas (joints)
eslabones (links)
q_1
q_2
robots = mecanismos actuados
Tipos de juntas
RP
RR
RRR
para un cuerpo rígido se tiene:
\mathrm{DOF}=\sum\text{libertades de los puntos}-\sum\text{restricciones independientes}
mientras que para un robot:
\mathrm{DOF}=\sum\text{libertades de los cuerpos}-\sum\text{restricciones independientes}
Grados de libertad (DOF)
Libertades de juntas en robots
DOF = grados de libertad del mecanismo.
\(N\) = número de eslabones.
\(J\) = número de juntas.
\(m\) = 3 (para mecanismos planares) y \(m\) = 6 (para mecanismos espaciales).
\(f_i\) = número de libertades de la junta \(i\).
\(c_i\) = número de restricciones de la junta \(i\).
\mathrm{DOF}=m(N-1)-\displaystyle\sum_{i=1}^{J}c_i=m(N-1-J)+\displaystyle\sum_{i=1}^{J}f_i
La fórmula de Grübler
\(m=3\)
\(N=4\)
\(J=4\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=1
\(m=3\)
\(N=4\)
\(J=4\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=1
\(m=3\)
\(N=4\)
\(J=4\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=1
\(m=3\)
\(N=5\)
\(J=4\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=4
\(m=3\)
\(N=5\)
\(J=4\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=1
\(m=3\)
\(N=6\)
\(J=7\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=4
\(m=3\)
\(N=5\)
\(J=4\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=1
\(m=3\)
\(N=6\)
\(J=7\)
\(f_i=1, \ i=1,2,3,4\)
\mathrm{DOF}=4
q_1
q_2
base fija
Brazos o manipuladores robóticos
configuración \(\sim\) DOF
q_1
q_2
efector final
q_1
q_2
manipulador serial
cadena cinemática abierta
manipulador paralelo
cadena cinemática cerrada
\mathrm{DOF}=15
\(m=6\)
\(N=17\)
\(J=21\) (9 revolutas y 12 esféricas)
\(f_i=1, \ i=1,\cdots,9\)
\(f_i=3, \ i=10,\cdots,21\)
El espacio de configuración
la configuración del robot es una especificación de la posición de todos sus puntos
\sim \mathrm{DOF}
\mathrm{DOF}=4
q_1
q_2
q_3
q_4
\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \\ q_3 \\ q_4 \end{bmatrix}
(vector de) configuración
\cdots
espacio de configuración \(\mathcal{C}\)
\mathbf{q} \in \mathcal{C}
\cdots
espacio de configuración \(\mathcal{C}\)
\mathbf{q} \in \mathcal{C}
aunque esto presenta un problema
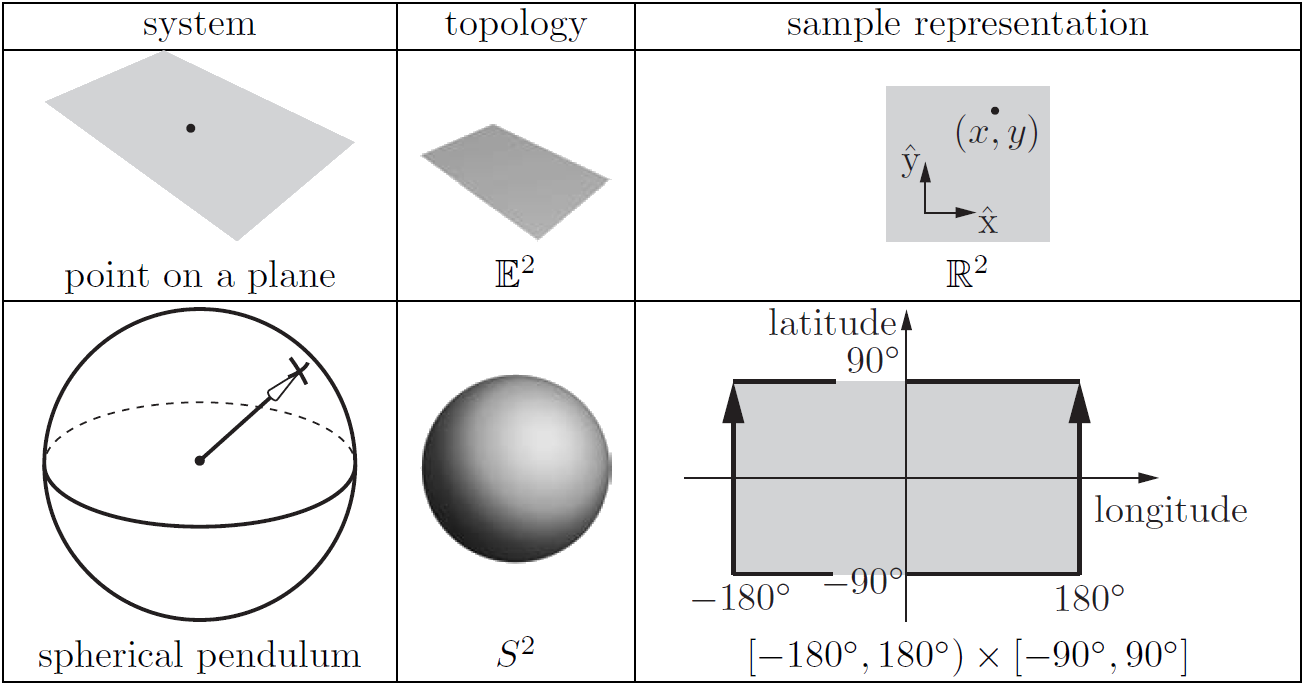
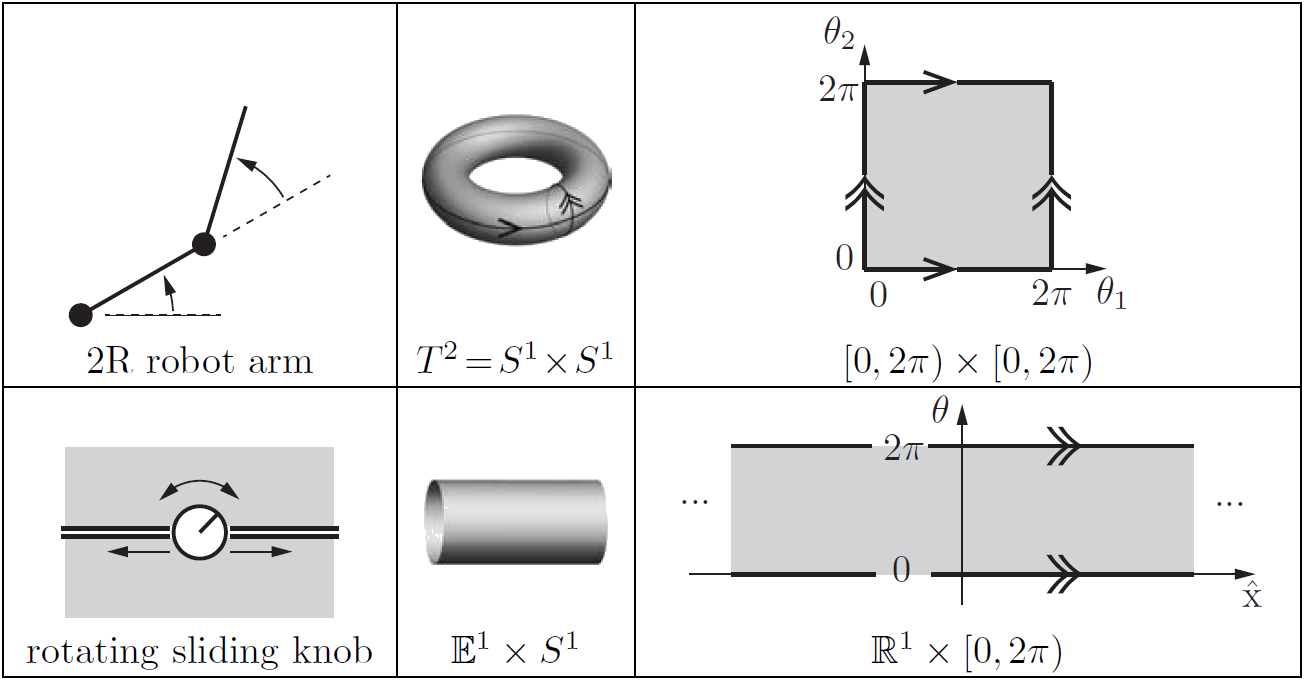
Topología del espacio de configuración
puede ser literalmente un obstáculo o una restricción
\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \\ q_3 \\ q_4 \end{bmatrix}=\begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \\ \theta_4 \end{bmatrix} \in\mathbb{R}^4
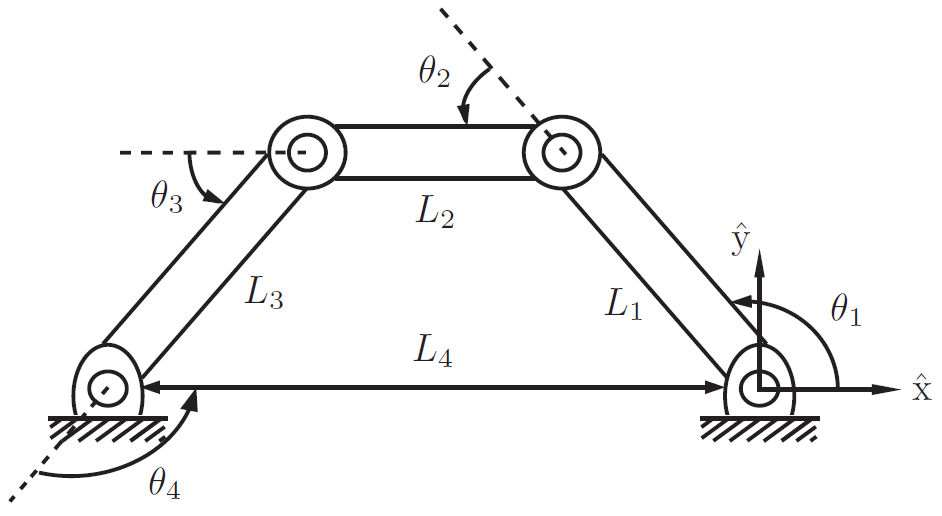
Restricciones de Pfaffian
\mathbf{h}\left(\mathbf{q}\right)=\mathbf{0}
\Rightarrow \mathbf{H}\left(\mathbf{q}\right)\dot{\mathbf{q}}=\mathbf{0}
L_1\cos(q_1)+L_2\cos(q_1+q_2)+\cdots+L_4\cos(q_1+\cdots+q_4)=0, \\
L_1\sin(q_1)+L_2\sin(q_1+q_2)+\cdots+L_4\sin(q_1+\cdots+q_4)=0, \\
q_1+q_2+q_3+q_4-2\pi=0.
\mathbf{h}\left(\mathbf{q}\right)=\mathbf{0}
\Rightarrow \mathbf{H}\left(\mathbf{q}\right)\dot{\mathbf{q}}=\mathbf{0}
L_1\cos(q_1)+L_2\cos(q_1+q_2)+\cdots+L_4\cos(q_1+\cdots+q_4)=0, \\
L_1\sin(q_1)+L_2\sin(q_1+q_2)+\cdots+L_4\sin(q_1+\cdots+q_4)=0, \\
q_1+q_2+q_3+q_4-2\pi=0.
restricción de configuración
\(\equiv\) restricción integrable
\(\equiv\) restricción holonómica
\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \\ q_3 \\ q_4 \end{bmatrix}=\begin{bmatrix} x \\ y \\ \theta \\ \phi \end{bmatrix} \in\mathbb{R}^4
\Rightarrow \mathbf{H}\left(\mathbf{q}\right)\dot{\mathbf{q}}=\mathbf{0}
\begin{bmatrix} 1 & 0 & 0 & -r\cos(q_3) \\ 0 & 1 & 0 & -r\sin(q_3) \end{bmatrix}\dot{\mathbf{q}}=\mathbf{0}
\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \\ q_3 \\ q_4 \end{bmatrix}=\begin{bmatrix} x \\ y \\ \theta \\ \phi \end{bmatrix} \in\mathbb{R}^4
\Rightarrow \mathbf{H}\left(\mathbf{q}\right)\dot{\mathbf{q}}=\mathbf{0}
\begin{bmatrix} 1 & 0 & 0 & -r\cos(q_3) \\ 0 & 1 & 0 & -r\sin(q_3) \end{bmatrix}\dot{\mathbf{q}}=\mathbf{0}
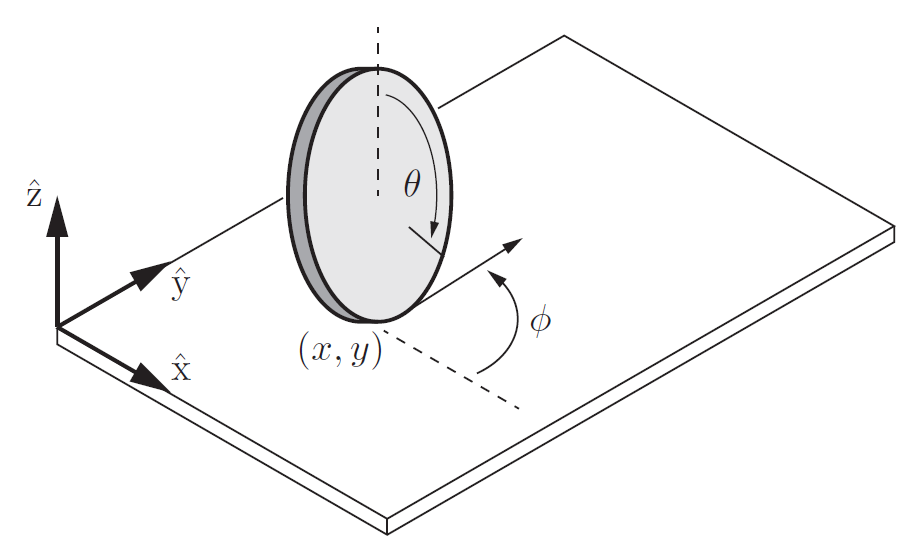
restricción de velocidad
\(\equiv\) restricción no integrable
\(\equiv\) restricción no holonómica
Los espacios de trabajo y de tarea
restricciones + obstáculos + limitantes físicas del robot
= espacio de trabajo
configuraciones alcanzables por el efector final
restricciones + obstáculos + limitantes físicas del robot
= espacio de trabajo
configuraciones alcanzables por el efector final
topología de \(\mathcal{C}\) difícil \(\to\) espacio de tarea para codificar la tarea de forma natural
ambos requieren de una especificación por parte del usuario
Ejemplos de espacio de trabajo
Intersección espacio trabajo y tarea
Un ejemplo completo
el robot SCARA
espacio de configuración:
q_1
q_2
q_3
q_4
\mathbf{q}\in\mathbb{R}^4\subset \mathcal{S}^1\times \mathcal{S}^1\times \mathcal{S}^1 \times \mathbb{E}^1
espacio de trabajo
espacio de tarea para pick and place:
(x,y,z)
(x,y,z,\psi) \subset SE(3)
\psi
MT3005 - Lecture 4 (2025)
By Miguel Enrique Zea Arenales
