Cinemática de cuerpos rígidos en 3D

MT3006 - Robótica 1

¿Qué ocurre en el caso 3D?
Veamos un ejemplo...

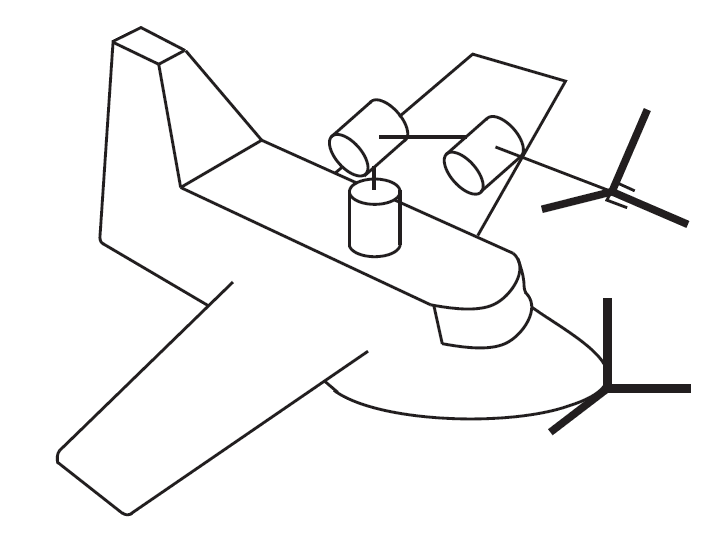


de nuevo se cumple
de nuevo se cumple
transformación homogénea
de nuevo se cumple
matriz de rotación
de nuevo se cumple
vector de traslación
de nuevo se cumple
vector de traslación
¿Cuál es la diferencia entonces?
2D
2
Incremento de grados de libertad
1
2D
3D
2
Incremento de grados de libertad
1
3
3
2D
3D
2
Incremento de grados de libertad
1
3
3
???
la matriz de rotación ya no tiene interpretación (única)
Interpretando la matriz de rotación
en 3D
Desde la definición
matriz de rotación ortogonal
columnas vectores ortonormales
Desde la definición
matriz de rotación ortogonal
columnas vectores ortonormales
Desde la definición
matriz de rotación ortogonal
columnas vectores ortonormales
vector que describe el eje \(x\) del marco \(\{B\}\) expresado en las coordenadas del marco \(\{A\}\)
Ejemplo
¿Cuál es la pose de \(\{B\}\) con respecto de \(\{I\}\)?
Ejemplo
¿Cuál es la pose de \(\{B\}\) con respecto de \(\{I\}\)?
Ejemplo
¿Cuál es la pose de \(\{B\}\) con respecto de \(\{I\}\)?
El teorema de rotación de Euler
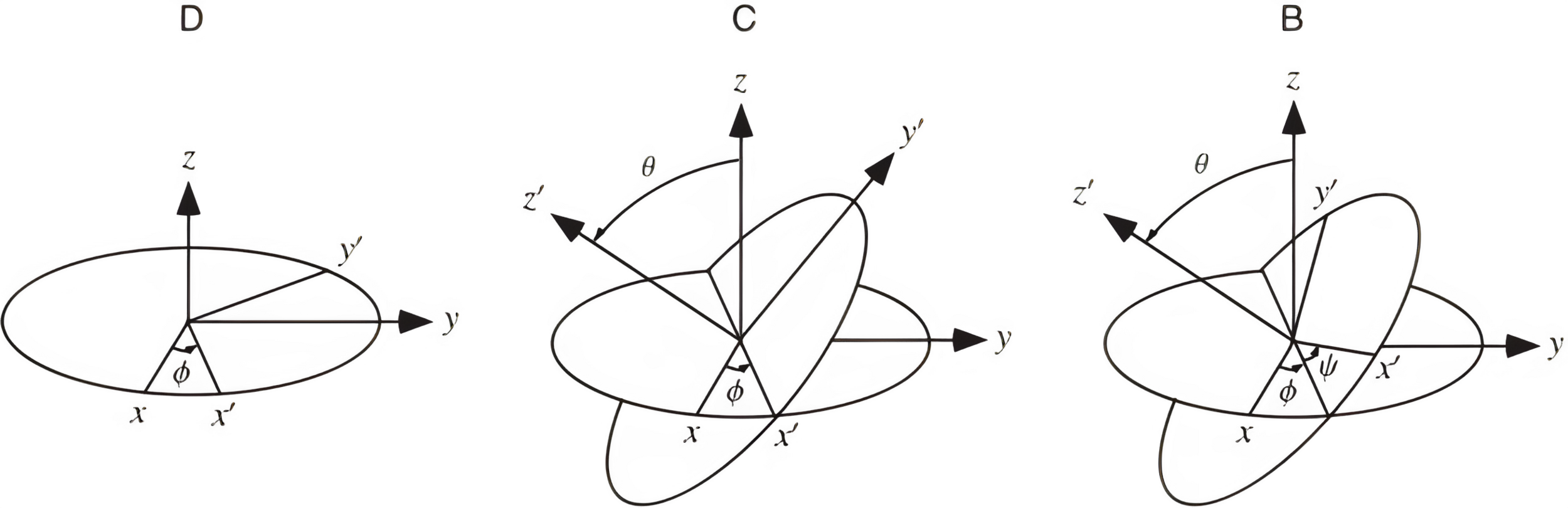
primera interpretación
El teorema de rotación de Euler

ángulos de Euler
Rx = rotx(theta)Ry = roty(theta)Rz = rotz(theta)12 posibles secuencias
Euler (se repite un eje): XYX, XZX, YXY, YZY, ZXZ, ZYZ.
Cardán (no se repiten ejes): XYZ, XZY, YZX, YXZ, ZXY, ZYX.
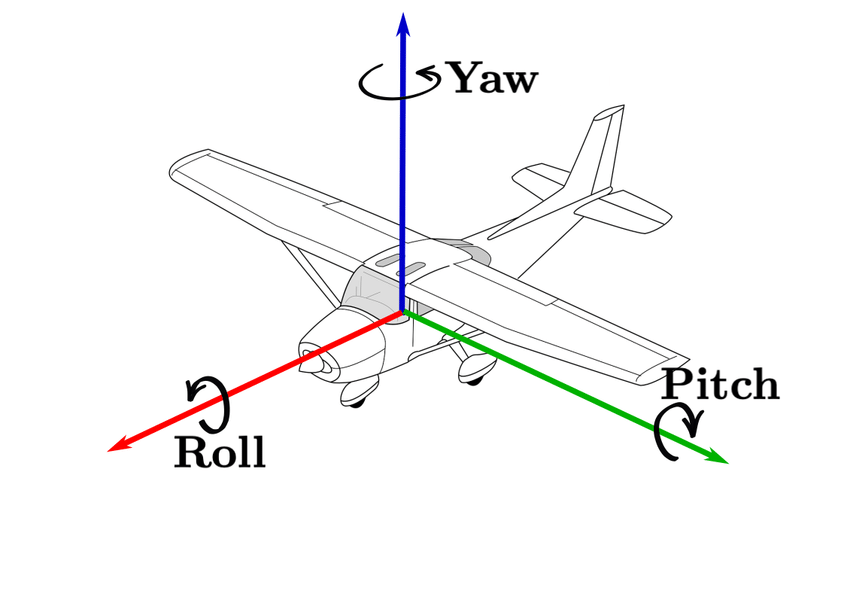



ZYX | XYZ
ángulos de navegación
(Tait-Bryan)
las rotaciones son con respecto a los ejes del marco de referencia inicial \(\rightarrow\) rotación pasiva o extrínseca
Interpretando la secuencia
Interpretando la secuencia

Interpretando la secuencia

las rotaciones son con respecto a los ejes (cambiantes) del cuerpo rígido \(\rightarrow\) rotación activa o intrínseca
Interpretando la secuencia
Interpretando la secuencia

Interpretando la secuencia

Ejemplo: generación de orientación
Suponga que una cámara se encuentra montada en la posición \((1,0,1)\) respecto al centro de un robot, alineada tal que su eje \(z\) coincide con el eje \(x\) del robot y su eje \(x\) coincide con el eje \(-y\) del robot. Determine la matriz de rotación \({^R}\mathbf{R}_C\) mediante:
- La definición de matriz de rotación.
- La secuencia ZYZ de ángulos de Euler.
- La secuencia roll-pitch-yaw.
- La secuencia XYZ de ángulos de Euler.
Ejemplo: generación de orientación
Ejemplo: generación de orientación
Ejemplo: generación de orientación
>> mt3005_clase2_euler_gen.mlx
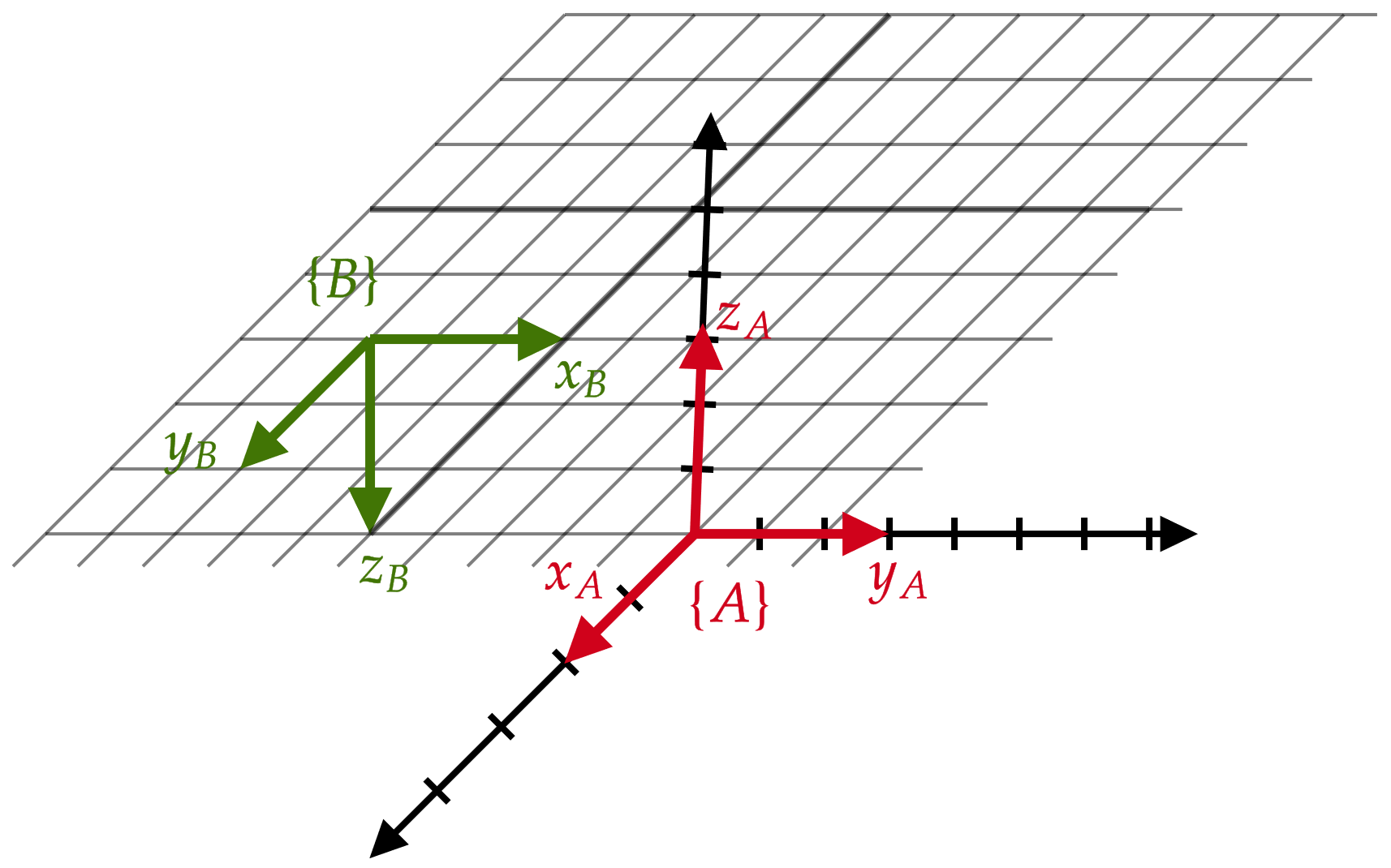
Ejemplo: interpretación
Los sensores de un avión retornaron que la pose actual del mismo \(\{B\}\) con respecto del marco de despegue \(\{A\}\) es
¿Cuál es el roll, pitch y yaw del avión?
>> mt3005_clase2_euler_avion.mlx
Es más sencillo emplear ángulos de Euler para interpretar la orientación que para generarla
¿Forma práctica para generar orientaciones y poses?
Transformaciones elementales
Traslación en \(x\)
Tx = transl(a, 0, 0)Traslación en \(y\)
Ty = transl(0, a, 0)Traslación en \(z\)
Tz = transl(0, 0, a)Rotación en \(x\)
Trx = trotx(theta)Rotación en \(y\)
Try = troty(theta)Rotación en \(z\)
Trz = trotz(theta)¿Cuál es la pose de \(\{B\}\) con respecto de \(\{A\}\)?
>> mt3005_clase2_transel.m
MT3005 - Lecture 2 (2025)
By Miguel Enrique Zea Arenales
MT3005 - Lecture 2 (2025)
- 117



