Cinemática de cuerpos rígidos en 2D
MT3006 - Robótica 1
Algunas situaciones típicas en robótica...
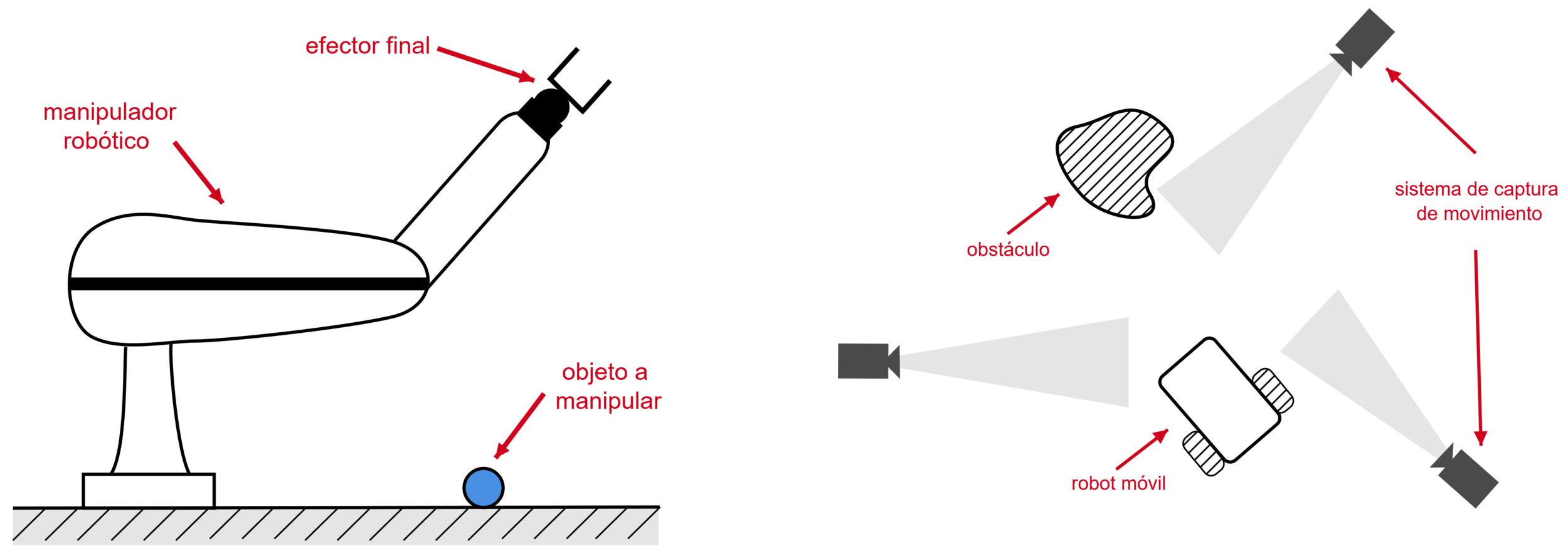
diversos agentes \(\Rightarrow\) diversas perspectivas
interacción e intercambio de información
lenguaje estándar y sistemático
diversos agentes \(\Rightarrow\) diversas perspectivas
interacción e intercambio de información
lenguaje estándar y sistemático
\(\Rightarrow\) Álgebra lineal
Cuerpos rígidos
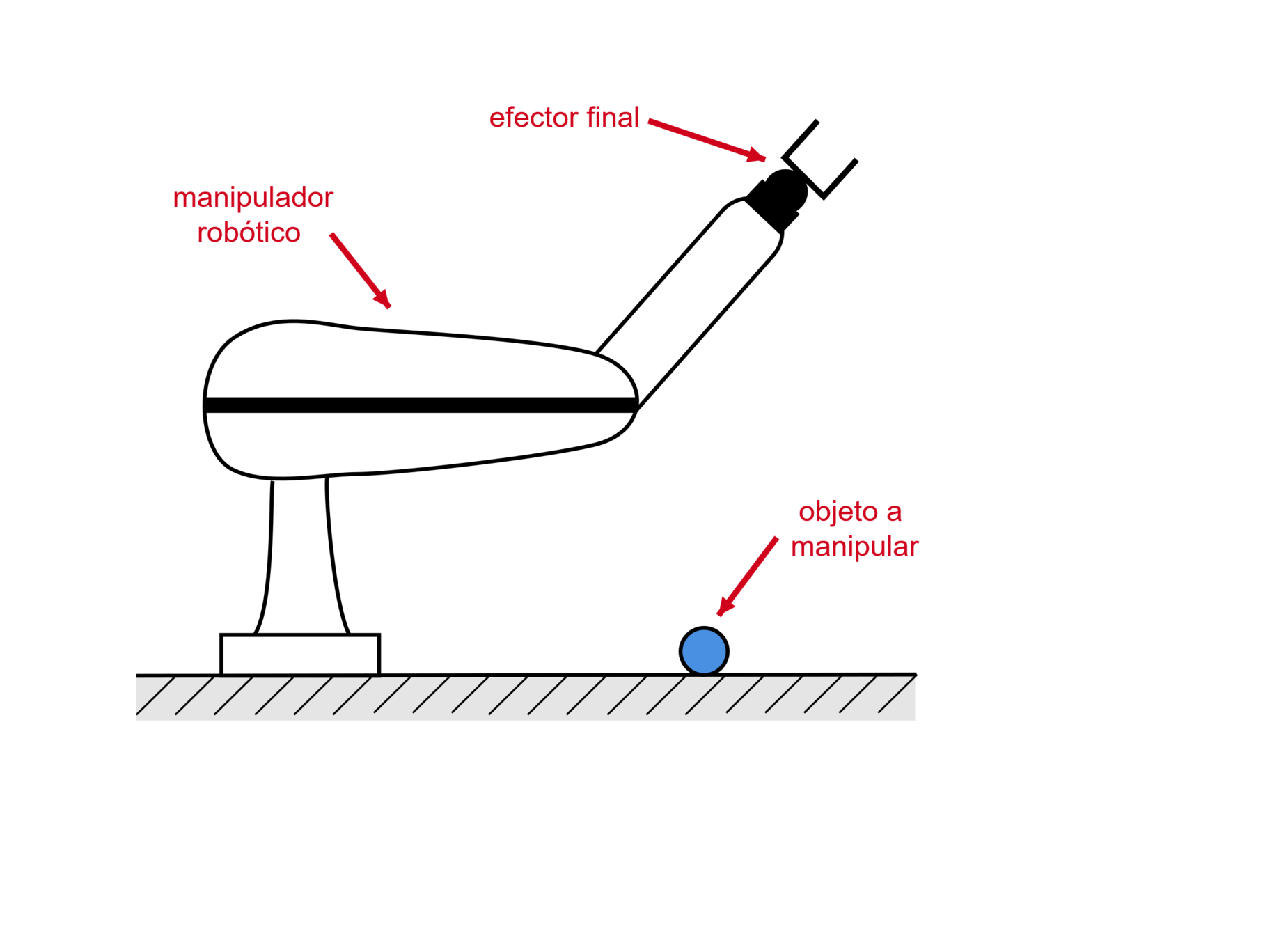
Cuerpos rígidos
Cuerpos rígidos
\text{rigidez } \Rightarrow d(p_i,p_j)=\mathrm{cte.}
y
x
z
y
x
z
y
x
z
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\boldsymbol{=}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
\boldsymbol{=}
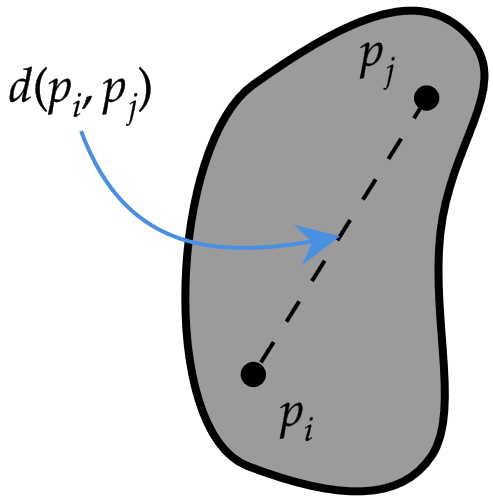
Marcos de referencia
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
marco inercial
body frame
Marcos de referencia
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
marco inercial
body frame
vectores en \(\{B\}\) forman un espacio vectorial
\(\hat{\mathbf{x}}_B, \hat{\mathbf{y}}_B, \hat{\mathbf{z}}_B\) base ortonormal para este espacio
Emplearemos marcos de referencia para ubicar cuerpos rígidos, describir su interacción y permitir el intercambio de información
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
p
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
p
{^M}\mathbf{x}
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
p
{^M}\mathbf{x}
nombre del vector
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
p
{^M}\mathbf{x}
marco de referencia en donde se define
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^M}\mathbf{x}
marco de referencia en donde se define
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^I}\mathbf{p}
{^M}\mathbf{x}
marco de referencia en donde se define
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^I}\mathbf{p}
{^B}\mathbf{p}
{^I}\mathbf{p}
distintos espacios vectoriales
\equiv
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^I}\mathbf{p}
debe existir para transformar de un espacio al otro
\mathcal{T}
y
x
z
\left\{I\right\}
\hat{\mathbf{y}}_B
\hat{\mathbf{x}}_B
\hat{\mathbf{z}}_B
\left\{B\right\}
{^B}\mathbf{p}
p
{^I}\mathbf{p}
{^I}\mathcal{T}_B
debe existir para transformar de un espacio al otro
\mathcal{T}
{^I}\mathcal{T}_B
marco destino
marco fuente
cuerpos rígidos \(\equiv\) transformaciones rígidas
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{{^B}\mathbf{p}\right\}
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{{^B}\mathbf{p}\right\}
x_I
y_I
z_I
\{I\}
p
x_A
z_A
y_A
\{A\}
z_B
y_B
x_B
\{B\}
x_C
y_C
z_C
\{C\}
x_R
y_R
z_R
\{R\}
x_I
y_I
z_I
\{I\}
p
x_A
z_A
y_A
\{A\}
z_B
y_B
x_B
\{B\}
x_C
y_C
z_C
\{C\}
x_R
y_R
z_R
\{R\}
{^I}\mathcal{T}_A
{^A}\mathcal{T}_B
{^B}\mathcal{T}_C
{^A}\mathcal{T}_R
x_I
y_I
z_I
\{I\}
p
x_A
z_A
y_A
\{A\}
z_B
y_B
x_B
\{B\}
x_C
y_C
z_C
\{C\}
x_R
y_R
z_R
\{R\}
{^I}\mathcal{T}_A
{^A}\mathcal{T}_B
{^B}\mathcal{T}_C
{^A}\mathcal{T}_R
{^C}\mathbf{p}
{^R}\mathbf{p}
¿Posición del obstáculo con respecto a la cámara B?
¿Posición del obstáculo con respecto al marco inercial?
¿Posición del obstáculo con respecto a la cámara B?
¿Posición del obstáculo con respecto al marco inercial?
{^B}\mathbf{p}={^B}\mathcal{T}_{\cancel{C}}\left\{ {^{\cancel{C}}}\mathbf{p} \right\}
{^I}\mathbf{p}={^I}\mathcal{T}_{\cancel{A}}\left\{ {^{\cancel{A}}}\mathcal{T}_{\cancel{R}}\left\{ {^{\cancel{R}}}\mathbf{p} \right\} \right\}
¿Posición del obstáculo con respecto a la cámara B, pero usando la información del robot?
¿Posición del obstáculo con respecto a la cámara B, pero usando la información del robot?
{^B}\mathbf{p}={^B}\mathcal{T}_{\cancel{A}}\left\{ {^{\cancel{A}}}\mathcal{T}_{\cancel{R}}\left\{ {^{\cancel{R}}}\mathbf{p} \right\} \right\}
\text{¿}{^B}\mathcal{T}_A \text{?} \rightarrow {^A}\mathcal{T}_B^{-1}
Matriz de transformación homogénea
{^I}\mathcal{T}_B \sim {^I}\mathbf{T}_B
toda transformación lineal tiene asociada una matriz
Entonces...
¿Posición del obstáculo con respecto a la cámara B?
{^B}\mathbf{p}={^B}\mathcal{T}_{\cancel{C}}\left\{ {^{\cancel{C}}}\mathbf{p} \right\}
\rightarrow \text{¿} {^B}\mathbf{p}={^B}\mathbf{T}_C {^C}\mathbf{p} \text{?}
Entonces...
¿Posición del obstáculo con respecto a la cámara B?
{^B}\mathbf{p}={^B}\mathcal{T}_{\cancel{C}}\left\{ {^{\cancel{C}}}\mathbf{p} \right\}
\rightarrow \text{¿} {^B}\mathbf{p}={^B}\mathbf{T}_C {^C}\mathbf{p} \text{?}
NO, aunque casi... (más adelante)
Pose = posición + orientación
{^I}\mathbf{T}_B
pose de \(\{B\}\) con respecto de \(\{I\}\)
la matriz como tal también posee información
Pose = posición + orientación
{^I}\mathbf{T}_B
pose de \(\{B\}\) con respecto de \(\{I\}\)
la matriz como tal también posee información
x_I
y_I
z_I
\{I\}
p
x_A
z_A
y_A
\{A\}
z_B
y_B
x_B
\{B\}
x_C
y_C
z_C
\{C\}
x_R
y_R
z_R
\{R\}
{^I}\mathcal{T}_A
{^A}\mathcal{T}_B
{^B}\mathcal{T}_C
{^A}\mathcal{T}_R
{^C}\mathbf{p}
{^R}\mathbf{p}
¿Ubicación de la cámara C con respecto al marco inercial?
¿Pose del robot con respecto al marco inercial?
¿Ubicación de la cámara C con respecto al marco inercial?
¿Pose del robot con respecto al marco inercial?
{^I}\mathbf{T}_C={^I}\mathbf{T}_{\cancel{A}} {^{\cancel{A}}}\mathbf{T}_{\cancel{B}} {^{\cancel{B}}}\mathbf{T}_C
{^I}\mathbf{T}_R={^I}\mathbf{T}_A {^A}\mathbf{T}_R
¿Qué es entonces la transformación homogénea en 2D?
x
y
\{I\}
x_B
y_B
\{B\}
x
y
\{I\}
\{B\}
x_B
y_B
(x,y)
x
y
\{I\}
\{B\}
x_B
y_B
(x,y)
\theta
x
y
\{I\}
\{B\}
x_B
y_B
(x,y)
\theta
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
\in \mathbb{R}^{3 \times 3}
x
y
\{I\}
\{B\}
x_B
y_B
(x,y)
\theta
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
\in \mathbb{R}^{3 \times 3}
3 grados de libertad
x
y
\{I\}
\{B\}
x_B
y_B
(x,y)
\theta
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
\in \mathbb{R}^{3 \times 3}
3 grados de libertad
IT_B = [ cos(theta), -sin(theta), x;
sin(theta), cos(theta), y;
0, 0, 1 ];
IT_B = transl2(x, y) * trot2(theta); % Robotics Toolbox
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
vector de traslación
posición de \(\{B\}\) con respecto a \(\{I\}\)
coordenadas del origen de \(\{B\}\)
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
matriz de rotación
orientación de \(\{B\}\) con respecto a \(\{I\}\)
vectores de los ejes de coordenadas para \(\{B\}\)
Las matrices de rotación junto con la multiplicación de matrices forman el grupo especial ortogonal
caso 2D
{^I}\mathbf{R}_B \in SO(2) \subset \mathbb{R}^{2 \times 2}
{^I}\mathbf{R}_B {^B}\mathbf{R}_C = {^I}\mathbf{R}_C
multiplicación entre rotaciones produce rotaciones
\left({^I}\mathbf{R}_B\right)^{-1}={^I}\mathbf{R}_B^\top\equiv {^B}\mathbf{R}_I
\mathrm{det}\left({^I}\mathbf{R}_B\right)=1
son matrices ortogonales
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}
ajuste por coordenadas homogéneas
ajuste por coordenadas homogéneas
{^I}\mathbf{T}_B=
\begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix}
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{ {^B}\mathbf{p} \right\}={^I}\mathbf{R}_B {^B}\mathbf{p} + {^I}\mathbf{o}_B
rotación + traslación
\equiv \underbrace{\begin{bmatrix} {^I}p_x \\ {^I}p_y \\ 1 \end{bmatrix}}_{{^I}\widetilde{\mathbf{p}}}=
\underbrace{\begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix}}_{{^I}\mathbf{T}_B}
\underbrace{\begin{bmatrix} {^B}p_x \\ {^B}p_y \\ 1 \end{bmatrix}}_{{^B}\widetilde{\mathbf{p}}}
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{ {^B}\mathbf{p} \right\}={^I}\mathbf{R}_B {^B}\mathbf{p} + {^I}\mathbf{o}_B
rotación + traslación
\equiv \underbrace{\begin{bmatrix} {^I}p_x \\ {^I}p_y \\ 1 \end{bmatrix}}_{{^I}\widetilde{\mathbf{p}}}=
\underbrace{\begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0}_{1\times 2} & 1 \end{bmatrix}}_{{^I}\mathbf{T}_B}
\underbrace{\begin{bmatrix} {^B}p_x \\ {^B}p_y \\ 1 \end{bmatrix}}_{{^B}\widetilde{\mathbf{p}}}
{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{ {^B}\mathbf{p} \right\}={^I}\mathbf{R}_B {^B}\mathbf{p} + {^I}\mathbf{o}_B
rotación + traslación
vectores en coordenadas homogéneas
\(\in \mathbb{P}^2 \subset \mathbb{R}^3\)
{^I}\tilde{\mathbf{p}}={^I}\mathbf{T}_B {^B}\tilde{\mathbf{p}}
Las matrices de transformación homogénea junto con la multiplicación de matrices forman el grupo especial euclideano
caso 2D
{^I}\mathbf{T}_B \in SE(2) \subset \mathbb{R}^{3 \times 3}
{^I}\mathbf{T}_B {^B}\mathbf{T}_C = {^I}\mathbf{T}_C
multiplicación entre transformaciones produce transformaciones
NO son matrices ortogonales
{^B}\mathbf{T}_I \equiv \left({^I}\mathbf{T}_B\right)^{-1} =
\begin{bmatrix} {^B}\mathbf{R}_I & -{^B}\mathbf{R}_I {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix} \ne {^I}\mathbf{T}_B^\top
Ejemplo
Suponga que un sensor de distancia instalado en un vehículo autónomo detecta una señal de tránsito en la posición \(\begin{bmatrix} 1 & 3 \end{bmatrix}^\top\). Este vehículo se encuentra en la posición \(\begin{bmatrix} 2 & 0 \end{bmatrix}^\top\) en el marco inercial (o global) con una orientación de \(\pi/3\). ¿Cuáles son las coordenadas globales de la señal de tránsito? (Asuma que los marcos del sensor de distancia y del robot son iguales)
>> mt3005_clase1_vehiculo2d.mlx
Addendum:
MT3005 - Lecture 1 (2025)
By Miguel Enrique Zea Arenales
