Algoritmos de cinemática inversa numérica
MT3005 - Robótica 1
¿Qué tenemos hasta ahora?
\mathbf{q}
\mathcal{K}\left(\mathbf{q}\right) \subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathcal{K}:\mathcal{C}\to \mathcal{T}
cinemática directa
\dot{\mathbf{q}}
{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}
{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
cinemática diferencial
\dot{\mathbf{q}}
{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}
{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
cinemática diferencial
¿A qué queremos llegar?
\mathbf{q}
\subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathcal{K}^{-1}:\mathcal{T}\to \mathcal{C}
cinemática inversa
especificación de la tarea
(se tiene)
referencias para los servos
(se quiere)
A pesar que el planteamiento es claro, se tiene un problema considerable
\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}
A pesar que el planteamiento es claro, se tiene un problema considerable
\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}
\mathcal{K}(\mathbf{q})
(en general) función extremadamente no lineal de la configuración
A pesar que el planteamiento es claro, se tiene un problema considerable
\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}
\mathcal{K}^{-1}
encontrar este mapeo resulta muy difícil y en muchos casos NO existe solución analítica
Ejemplo: cinemática inversa analítica
\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \end{bmatrix} \in \mathbb{R}^2
\mathcal{T} \sim (x,y) \subset SE(2)
espacio de configuración
espacio de tarea
Ejemplo: cinemática inversa analítica
\begin{array}{c|c|c|c}
\theta_j & d_j & a_j & \alpha_j \\ \hline
q_1 & 0 & a_1 & 0 \\ \hline
q_2 & 0 & a_2 & 0 \\
\end{array}
R
R
manipulador RR
>> mt3005_clase9_manipuladorRR.mlx
{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\mathbf{J}(\mathbf{q})=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}
{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\mathcal{K}\left(\mathbf{q}\right)=
{^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}=
\begin{bmatrix} a_1\cos(q_1)+a_2\cos(q_1+q_2) \\ a_1\sin(q_1)+a_2\sin(q_1+q_2) \end{bmatrix}
{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\mathcal{K}\left(\mathbf{q}\right)=
{^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}=
\begin{bmatrix} a_1\cos(q_1)+a_2\cos(q_1+q_2) \\ a_1\sin(q_1)+a_2\sin(q_1+q_2) \end{bmatrix}
\Rightarrow \mathbf{q}=
\mathcal{K}^{-1}\left({^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}\right)
empleando trigonometría y métodos algebráicos
q_1=\mathrm{atan2}\left(\dfrac{y_E}{x_E}\right)-\mathrm{atan2}\left(\dfrac{a_2\sin(q_2)}{a_1+a_2\cos(q_2)}\right)
q_2=\arccos\left( \dfrac{x_E^2+y_E^2-a_1^2-a_2^2}{2 a_1a_2}\right)
empleando trigonometría y métodos algebráicos
q_1=\mathrm{atan2}\left(\dfrac{y_E}{x_E}\right)-\mathrm{atan2}\left(\dfrac{a_2\sin(q_2)}{a_1+a_2\cos(q_2)}\right)
q_2=\arccos\left( \dfrac{x_E^2+y_E^2-a_1^2-a_2^2}{2 a_1a_2}\right)
\(\arctan\) pero válida en \((-\pi, \pi]\) (programación)
las expresiones trigonométricas muestran múltiples soluciones al problema
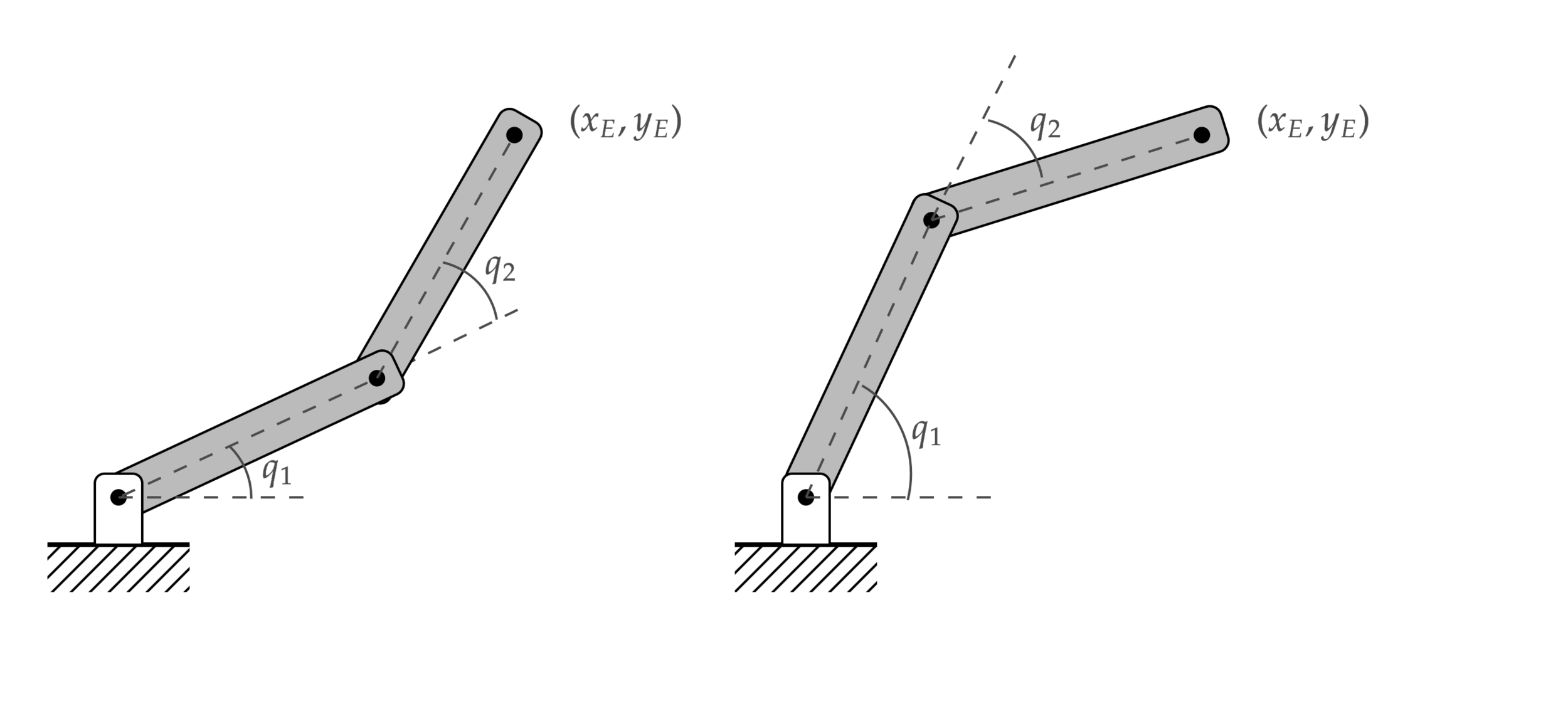
si bien hay casos en donde podemos encontrar la solución analítica, hacerlo no es tan buena idea
si bien hay casos en donde podemos encontrar la solución analítica, hacerlo no es tan buena idea
\(\to\) expresiones complejas e individuales, incluso para manipuladores triviales
\(\to\) solución dada en lazo abierto (no corrige errores)
¿Qué hacemos entonces?
emplear algoritmos basados en control (lazo cerrado) para encontrar la cinemática inversa de forma numérica
\(\mathcal{K}^{-1}\) como un problema de control
pose del efector final como vector*
{^B}\boldsymbol{\xi}_E(t)=\begin{bmatrix} {^B}\mathbf{o}_E\left(\mathbf{q}(t)\right) \\ {^B}\boldsymbol{\theta}_E\left(\mathbf{q}(t)\right) \end{bmatrix}
pose del efector final como vector*
{^B}\boldsymbol{\xi}_E(t)=\begin{bmatrix} {^B}\mathbf{o}_E\left(\mathbf{q}(t)\right) \\ {^B}\boldsymbol{\theta}_E\left(\mathbf{q}(t)\right) \end{bmatrix}
* orientación del efector final pero en forma vectorial
pose del efector final como vector*
{^B}\boldsymbol{\xi}_E(t)=\begin{bmatrix} {^B}\mathbf{o}_E\left(\mathbf{q}(t)\right) \\ {^B}\boldsymbol{\theta}_E\left(\mathbf{q}(t)\right) \end{bmatrix}
\Rightarrow {^B}\dot{\boldsymbol{\xi}}_E(t)\equiv{^B}\dot{\boldsymbol{\xi}}_E =\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
* orientación del efector final pero en forma vectorial
\mathbf{e}=\begin{bmatrix} \mathbf{e}_p \\ \mathbf{e}_o \end{bmatrix}=\boldsymbol{\xi}_d - {^B}\boldsymbol{\xi}_E
\mathbf{e}=\begin{bmatrix} \mathbf{e}_p \\ \mathbf{e}_o \end{bmatrix}=\boldsymbol{\xi}_d - {^B}\boldsymbol{\xi}_E
\Rightarrow \dot{\mathbf{e}}=\dot{\boldsymbol{\xi}}_d - {^B}\dot{\boldsymbol{\xi}}_E=\dot{\boldsymbol{\xi}}_d - \mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
\mathbf{e}=\begin{bmatrix} \mathbf{e}_p \\ \mathbf{e}_o \end{bmatrix}=\boldsymbol{\xi}_d - {^B}\boldsymbol{\xi}_E
error
error de posición
error de orientación
pose de E.F. deseada
\Rightarrow \dot{\mathbf{e}}=\dot{\boldsymbol{\xi}}_d - {^B}\dot{\boldsymbol{\xi}}_E=\dot{\boldsymbol{\xi}}_d - \mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
dinámica del error
suposición: puede controlarse \(\dot{\mathbf{q}}\) \(\Rightarrow\) \(\dot{\mathbf{q}}\) es la entrada de control
\dot{\mathbf{e}}=\dot{\boldsymbol{\xi}}_d - {^B}\dot{\boldsymbol{\xi}}_E=\dot{\boldsymbol{\xi}}_d - \mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
suposición: puede controlarse \(\dot{\mathbf{q}}\) \(\Rightarrow\) \(\dot{\mathbf{q}}\) es la entrada de control
\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
\dot{\mathbf{e}}=\dot{\boldsymbol{\xi}}_d - {^B}\dot{\boldsymbol{\xi}}_E=\dot{\boldsymbol{\xi}}_d - \mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
suposición: puede controlarse \(\dot{\mathbf{q}}\) \(\Rightarrow\) \(\dot{\mathbf{q}}\) es la entrada de control
\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
\dot{\mathbf{e}}=\dot{\boldsymbol{\xi}}_d - {^B}\dot{\boldsymbol{\xi}}_E=\dot{\boldsymbol{\xi}}_d - \mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
linealización por feedback
suposición: puede controlarse \(\dot{\mathbf{q}}\) \(\equiv\) \(\dot{\mathbf{q}}\) es la entrada de control
entonces se obtiene el sistema LTI
\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
\dot{\mathbf{e}}+\mathbf{K}\mathbf{e}=\mathbf{0} \Rightarrow \dot{\mathbf{e}}=-\mathbf{K}\mathbf{e}
suposición: puede controlarse \(\dot{\mathbf{q}}\) \(\equiv\) \(\dot{\mathbf{q}}\) es la entrada de control
linealización por feedback
entonces se obtiene el sistema LTI
\dot{\mathbf{e}}+\mathbf{K}\mathbf{e}=\mathbf{0} \Rightarrow \dot{\mathbf{e}}=-\mathbf{K}\mathbf{e}
\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
el sistema es globalmente (exponencialmente) asintóticamente estable siempre y cuando \(\mathbf{K}\succ 0\) (positiva definida), usualmente una matriz diagonal
\mathbf{J}^\dagger(\mathbf{q})
\mathbf{J}^\dagger(\mathbf{q})
\(\approx \mathbf{J}^{-1}(\mathbf{q})\), numéricamente lo más cercano a la inversa de una matriz no cuadrada
pseudo-inversa de Moore Penrose
\mathbf{J}^\dagger(\mathbf{q})
\(\approx \mathbf{J}^{-1}(\mathbf{q})\), numéricamente lo más cercano a la inversa de una matriz no cuadrada
pseudo-inversa de Moore Penrose
\mathbf{J}^\dagger = \mathbf{J}^\top \left(\mathbf{J} \mathbf{J}^\top\right)^{-1}
\mathbf{J}^\dagger = \left(\mathbf{J}^\top \mathbf{J}\right)^{-1} \mathbf{J}^\top
para jacobianos "gordos"
(más columnas que filas)
para jacobianos "flacos"
(más filas que columnas)
\mathbf{J}^\dagger(\mathbf{q})
\(\approx \mathbf{J}^{-1}(\mathbf{q})\), numéricamente lo más cercano a la inversa de una matriz no cuadrada
pseudo-inversa de Moore Penrose
\mathbf{J}^\dagger = \mathbf{J}^\top \left(\mathbf{J} \mathbf{J}^\top\right)^{-1}
\mathbf{J}^\dagger = \left(\mathbf{J}^\top \mathbf{J}\right)^{-1} \mathbf{J}^\top
para jacobianos "gordos"
(más columnas que filas)
para jacobianos "flacos"
(más filas que columnas)
Ji = pinv(J)\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
servos
\dot{\mathbf{q}}=\mathbf{J}^\dagger(\mathbf{q})\left( \dot{\boldsymbol{\xi}}_d + \mathbf{K}\mathbf{e}\right)
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\left( \dot{\boldsymbol{\xi}}_d[k] + \mathbf{K}\mathbf{e}_k\right)\Delta t
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\left( \boldsymbol{\xi}_d[k] + \mathbf{K}_e\mathbf{e}_k\right)
servos
típicamente reciben setpoints de posición
+ forward Euler o RK4
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\left( \boldsymbol{\xi}_d[k] + \mathbf{K}_e\mathbf{e}_k\right)
arquitectura general de los algoritmos de cinemática inversa
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\left( \boldsymbol{\xi}_d[k] + \mathbf{K}_e\mathbf{e}_k\right)
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_v^\dagger(\mathbf{q}_k)\left( \mathbf{o}_d[k] + \mathbf{K}_p\mathbf{e}_p[k]\right)
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_\omega^\dagger(\mathbf{q}_k)\left( \boldsymbol{\theta}_d[k] + \mathbf{K}_o\mathbf{e}_o[k]\right)
arquitectura general de los algoritmos de cinemática inversa
posición
orientación
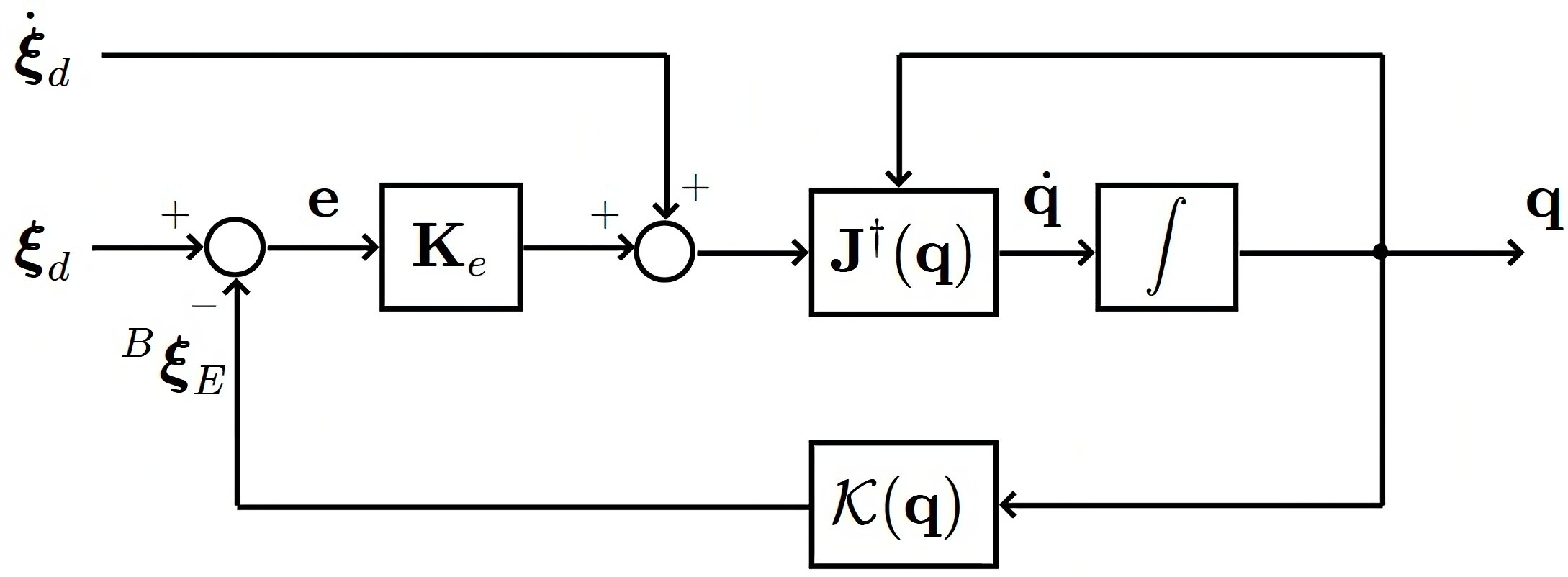
Arquitectura del controlador
"sensor"
"planta"
término feedforward
control "proporcional"
Arquitectura del controlador
Otras "pseudo-inversas"
si \(\boldsymbol{\xi}_d=\mathrm{cte.}\) entonces \(\dot{\boldsymbol{\xi}}_d=\mathbf{0}\) y
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\mathbf{K}_e\mathbf{e}_k
Otras "pseudo-inversas"
si \(\boldsymbol{\xi}_d=\mathrm{cte.}\) entonces \(\dot{\boldsymbol{\xi}}_d=\mathbf{0}\) y
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\mathbf{K}_e\mathbf{e}_k
\mathbf{J}^\dagger \to \mathbf{J}^\top\left(\mathbf{J}\mathbf{J}^\top+\lambda^2\mathbf{I}\right)^{-1}
Damped Least-Squares o Levenberg-Marquadt
\(\lambda>0\) y pequeña, mejora el performance en singularidades
Otras "pseudo-inversas"
si \(\boldsymbol{\xi}_d=\mathrm{cte.}\) entonces \(\dot{\boldsymbol{\xi}}_d=\mathbf{0}\) y
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger(\mathbf{q}_k)\mathbf{K}_e\mathbf{e}_k
\mathbf{J}^\dagger \to \mathbf{J}^\top\left(\mathbf{J}\mathbf{J}^\top+\lambda^2\mathbf{I}\right)^{-1}
\mathbf{J}^\dagger \to \mathbf{J}^\top
Damped Least-Squares o Levenberg-Marquadt
\(\lambda>0\) y pequeña, mejora el performance en singularidades
Traspuesta
numéricamente eficiente, garantiza que el origen \(\mathbf{e}=\mathbf{0}\) es asintóticamente estable bajo la función de Lyapunov \(V(\mathbf{e})=\dfrac{1}{2}\mathbf{e}^\top\mathbf{K}_e \mathbf{e}\)
de nuevo el algoritmo puede separase
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_v^\dagger(\mathbf{q}_k)\mathbf{K}_p\mathbf{e}_p[k]
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_\omega^\dagger(\mathbf{q}_k)\mathbf{K}_o\mathbf{e}_o[k]
posición
orientación
de nuevo el algoritmo puede separase
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_v^\dagger(\mathbf{q}_k)\mathbf{K}_p\mathbf{e}_p[k]
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_\omega^\dagger(\mathbf{q}_k)\mathbf{K}_o\mathbf{e}_o[k]
\mathbf{K}_e=\begin{bmatrix} \mathbf{K}_p & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_o \end{bmatrix}
\mathbf{e}_p[k]=\mathbf{o}_d-{^B}\mathbf{o}_E\left(\mathbf{q}_k\right)
\mathbf{e}_o[k]=\boldsymbol{\theta}_d-{^B}\boldsymbol{\theta}_E\left(\mathbf{q}_k\right)
posición
orientación
de nuevo el algoritmo puede separase
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_v^\dagger(\mathbf{q}_k)\mathbf{K}_p\mathbf{e}_p[k]
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_\omega^\dagger(\mathbf{q}_k)\mathbf{K}_o\mathbf{e}_o[k]
\mathbf{K}_e=\begin{bmatrix} \mathbf{K}_p & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_o \end{bmatrix}
\mathbf{e}_p[k]=\mathbf{o}_d-{^B}\mathbf{o}_E\left(\mathbf{q}_k\right)
\mathbf{e}_o[k]=\boldsymbol{\theta}_d-{^B}\boldsymbol{\theta}_E\left(\mathbf{q}_k\right)
posición
orientación
\boldsymbol{\succ} 0
\boldsymbol{\succ} 0
\boldsymbol{\xi}_d \sim \mathbf{T}_d
{^B}\mathbf{T}_E\left(\mathbf{q}_k\right)
de nuevo el algoritmo puede separase
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_v^\dagger(\mathbf{q}_k)\mathbf{K}_p\mathbf{e}_p[k]
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_\omega^\dagger(\mathbf{q}_k)\mathbf{K}_o\mathbf{e}_o[k]
\mathbf{K}_e=\begin{bmatrix} \mathbf{K}_p & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_o \end{bmatrix}
\mathbf{e}_p[k]=\mathbf{o}_d-{^B}\mathbf{o}_E\left(\mathbf{q}_k\right)
\mathbf{e}_o[k]=\boldsymbol{\theta}_d-{^B}\boldsymbol{\theta}_E\left(\mathbf{q}_k\right)
posición
orientación
\boldsymbol{\succ} 0
\boldsymbol{\succ} 0
\boldsymbol{\xi}_d \sim \mathbf{T}_d
{^B}\mathbf{T}_E\left(\mathbf{q}_k\right)
\mathbf{???}
Una alternativa para obtener intuición detrás de los algoritmos
idea fundamental (prestando atención sólo a la posición)
{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}
idea fundamental (prestando atención sólo a la posición)
{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}
\approx \dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}
idea fundamental (prestando atención sólo a la posición)
{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}
\Delta {^B}\mathbf{o}_E=\mathbf{J}_v(\mathbf{q}) \Delta \mathbf{q}
\Delta \mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}) \Delta {^B}\mathbf{o}_E
\approx \dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}
\(\mathbf{T}_d\equiv\) meta
\({^B}\mathbf{T}_E(\mathbf{q})\)
efector final
el algoritmo debe llevar al efector final a la pose deseada o "meta"
\(\mathbf{T}_d\equiv\) meta
\({^B}\mathbf{T}_E(\mathbf{q})\)
efector final
Nota 1: el robot sólo puede cambiar su configuración
Nota 2: por el momento nos interesa sólo la posición
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
configuración actual: \(\mathbf{q}_1\)
¿Cuál es la discrepancia entre la posición deseada y la posición actual?
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
configuración actual: \(\mathbf{q}_1\)
¿Cuál es la discrepancia entre la posición deseada y la posición actual?
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
configuración actual: \(\mathbf{q}_1\)
\mathbf{e}_p=\mathbf{o}_d-{^B}\mathbf{o}_E(\mathbf{q}_1)
¿Cuál es la discrepancia entre la posición deseada y la posición actual?
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
configuración actual: \(\mathbf{q}_1\)
\mathbf{e}_p=\mathbf{o}_d-{^B}\mathbf{o}_E(\mathbf{q}_1) \sim \Delta {^B}\mathbf{o}_E
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
configuración actual: \(\mathbf{q}_1\)
¿Hacia dónde, potencialmente, puede moverse el robot?
¿Hacia dónde, potencialmente, puede moverse el robot?
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
configuración actual: \(\mathbf{q}_1\)
\mathbf{J}_v(\mathbf{q}_1)
entonces el robot hace un movimiento pequeño tomando todo en consideración
configuración actual: \(\mathbf{q}_2\)
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
\mathbf{J}_v(\mathbf{q}_1)
entonces el robot hace un movimiento pequeño tomando todo en consideración
configuración actual: \(\mathbf{q}_2\)
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
\mathbf{J}_v(\mathbf{q}_1)
\mathbf{q}_2=\mathbf{q}_1+\Delta\mathbf{q}
\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \Delta {^B}\mathbf{o}_E \\
\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \mathbf{e}_p
{^B}\mathbf{o}_E(\mathbf{q}_1)
\mathbf{o}_d
\mathbf{J}_v(\mathbf{q}_1)
entonces el robot hace un movimiento pequeño tomando todo en consideración
configuración actual: \(\mathbf{q}_2\)
\mathbf{q}_2=\mathbf{q}_1+\Delta\mathbf{q}
\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \Delta {^B}\mathbf{o}_E \\
\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \mathbf{e}_p
\mathbf{q}_2=\mathbf{q}_1+\mathbf{J}^\dagger_v(\mathbf{q}_1)\mathbf{e}_p
y se repite el proceso hasta que el error/discrepancia sea lo suficientemente pequeño
puede obtenerse una intuición similar para la orientación o la pose completa
Regresando a los algoritmos
Ejemplo: cinemática inversa de posición
\mathcal{T}: \ {^B}\mathbf{o}_E \subset {^B}\mathbf{T}_E\left(\mathbf{q}\right)
PUMA 560
\mathcal{C}: \ \mathbf{q} \in \mathbb{R}^6
nos interesa obtener una rutina numérica para la cinemática inversa de posición
se asume que se tiene acceso a:
mdl_p560;
p560.fkine(q);
p560.jacob0(q);% Inicialización del algoritmo
eps = 1e-06; % tolerancia del error
N = 100; % número (máximo) de iteraciones
od = Td(1:3, 4); % posición deseada del EF
q_k = q0; % configuración inicial
T = p560.fkine(q_k').T;
o_k = T(1:3, 4); % posición incial del EF
ep = od - o_k; % error inicial
n = 0;
Q = q0; % array para almacenar la evolución de las iteraciones
% El algoritmo iterativo se repite hasta que el error llegue a la
% tolerancia deseada o se supere el número máximo de iteraciones
while( (norm(ep) > eps) && (n < N) )
T = p560.fkine(q_k').T;
o_k = T(1:3, 4); % posición actual del EF
ep = od - o_k; % error actual
J = p560.jacob0(q_k'); % jacobiano completo
Jv = J(1:3, :); % jacobiano de posición
% Opciones de algoritmos
Ji = pinv(Jv); % pseudo-inversa
%Ji = Jv' / (Jv*Jv' + (0.1^2)*eye(3)); % Levenberg-Marquadt
%Ji = Jv'; % traspuesta
q_k = q_k + Ji * ep; % algoritmo de cinemática inversa
n = n + 1;
Q = [Q, q_k]; % se almacena el histórico de la configuración
end
>> mt3005_clas9_pumaiknum.m
Cinemática inversa de orientación
regresando al error de orientación
\mathbf{e}_o[k]=\boldsymbol{\theta}_d-{^B}\boldsymbol{\theta}_E\left(\mathbf{q}_k\right)
Cinemática inversa de orientación
regresando al error de orientación
\mathbf{e}_o[k]=\boldsymbol{\theta}_d-{^B}\boldsymbol{\theta}_E\left(\mathbf{q}_k\right)
depende de la representación
???
Cinemática inversa de orientación
regresando al error de orientación
\mathbf{e}_o[k]=\boldsymbol{\theta}_d-{^B}\boldsymbol{\theta}_E\left(\mathbf{q}_k\right)
depende de la representación
\(\to \mathbf{R}\)? no, muy complicado de operar
\(\to (\phi,\theta,\psi)\)? no, presentan singularidades
\(\to (\hat{\boldsymbol{\omega}},\theta)\)? no, hay que regresar a \(\mathbf{R}\) para operar
???
¿Solución? cuaterniones unitarios
¿Solución? cuaterniones unitarios
\mathcal{Q}*\mathcal{Q}^{-1}=\{1,\mathbf{0}\}
recordemos que
\mathcal{Q}_1*\mathcal{Q}_2^{-1}=\{1,\mathbf{0}\}
por lo que si
¿Solución? cuaterniones unitarios
\mathcal{Q}*\mathcal{Q}^{-1}=\{1,\mathbf{0}\}
recordemos que
\mathcal{Q}_1*\mathcal{Q}_2^{-1}=\{1,\mathbf{0}\}
por lo que si
\(\Rightarrow \mathcal{Q}_1\) y \(\mathcal{Q}_2\) son iguales \(\equiv\) están alineados
\boldsymbol{\epsilon}=\mathbf{0}
¿Solución? cuaterniones unitarios
\mathcal{Q}*\mathcal{Q}^{-1}=\{1,\mathbf{0}\}
recordemos que
\mathcal{Q}_1*\mathcal{Q}_2^{-1}=\{1,\mathbf{0}\}
por lo que si
\(\Rightarrow \mathcal{Q}_1\) y \(\mathcal{Q}_2\) son iguales \(\equiv\) están alineados
\boldsymbol{\epsilon}=\mathbf{0}
por lo tanto \(\boldsymbol{\epsilon}\to\mathbf{0}\) conforme los cuaterniones se alinean
idea:
\mathcal{Q}_d \sim \mathbf{R}_d
\mathcal{Q}\left(\mathbf{q}_k\right) \sim {^B}\mathbf{R}_E\left(\mathbf{q}_k\right)
idea:
\mathcal{Q}_d \sim \mathbf{R}_d
\mathcal{Q}\left(\mathbf{q}_k\right) \sim {^B}\mathbf{R}_E\left(\mathbf{q}_k\right)
\mathcal{Q}_e[k] = \mathcal{Q}_d * \mathcal{Q}^{-1}\left(\mathbf{q}_k\right) \\
=\{ \eta_e[k], \boldsymbol{\epsilon}_e[k] \}
idea:
\mathcal{Q}_d \sim \mathbf{R}_d
\mathcal{Q}\left(\mathbf{q}_k\right) \sim {^B}\mathbf{R}_E\left(\mathbf{q}_k\right)
\mathcal{Q}_e[k] = \mathcal{Q}_d * \mathcal{Q}^{-1}\left(\mathbf{q}_k\right) \\
=\{ \eta_e[k], \boldsymbol{\epsilon}_e[k] \}
\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}_\omega^\dagger(\mathbf{q}_k)\mathbf{K}_o \mathbf{e}_o[k]
\mathbf{e}_o[k]=\boldsymbol{\epsilon}_e[k]
Un último detalle IMPORTANTE
\mathbf{q}_0
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\
=\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
\mathbf{q}_f
\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\
=\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
\mathbf{q}_f
cinemática inversa
{^B}\mathbf{T}_E \to \mathbf{T}_d
(en general)
\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\
=\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
\mathbf{q}_f
cinemática inversa
{^B}\mathbf{T}_E \to \mathbf{T}_d
(en general)
\mathbf{q} \to \mathbf{q}_d
NO necesariamente
\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\
=\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}
Un último detalle IMPORTANTE
\mathbf{q}_0
\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)=
\begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}
\mathbf{q}_f
cinemática inversa
{^B}\mathbf{T}_E \to \mathbf{T}_d
(en general)
\mathbf{q} \to \mathbf{q}_d
NO necesariamente
\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\
=\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}
Referencias
- Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares methods.pdf
MT3005 - Lecture 9 (2025)
By Miguel Enrique Zea Arenales
