Cinemática diferencial de manipuladores seriales
MT3005 - Robótica 1
¿Qué tenemos hasta ahora?
\mathbf{q}
\mathcal{K}\left(\mathbf{q}\right) \subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathbf{q}
\mathcal{K}\left(\mathbf{q}\right) \subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathcal{K}:\mathcal{C}\to \mathcal{T}
cinemática directa
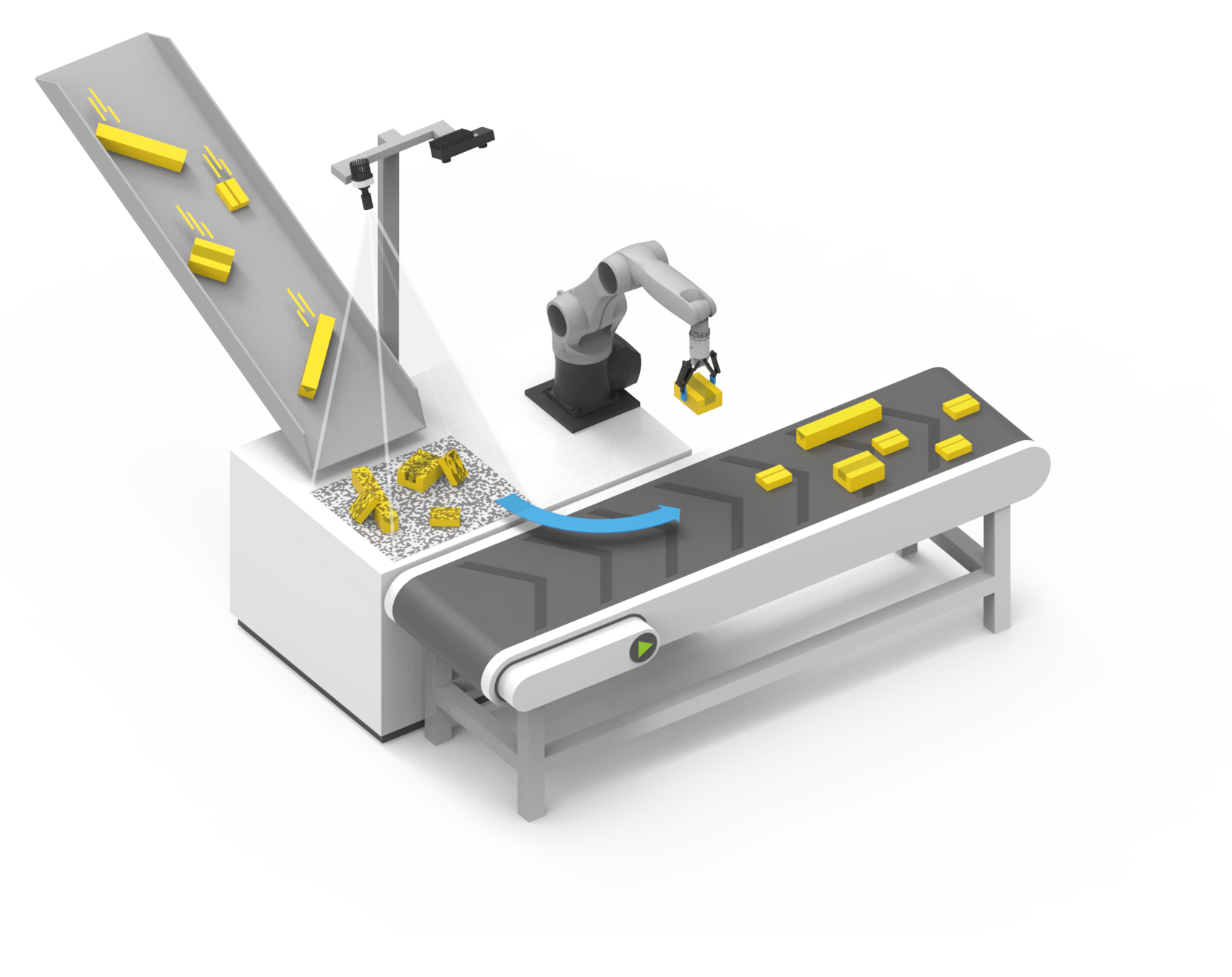
mapeo útil, pero impráctico
¿Qué ocurre en una aplicación real?
mapeo útil, pero impráctico
¿Qué ocurre en una aplicación real?
especificamos la tarea \(\mathcal{T}\)
mapeo útil, pero impráctico
¿Qué ocurre en una aplicación real?
especificamos la tarea \(\mathcal{T}\)
¿Cómo debe ejecutarla el robot? \(\mathcal{C}\)
mapeo útil, pero impráctico
¿Qué ocurre en una aplicación real?
especificamos la tarea \(\mathcal{T}\)
¿Cómo debe ejecutarla el robot? \(\mathcal{C}\)
¿Cuál es el mapeo que realmente queremos entonces?
\mathbf{q}
\subseteq {^B}\mathbf{T}_E(\mathbf{q})
especificación de la tarea
(se tiene)
referencias para los servos
(se quiere)
\mathbf{q}
\subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathcal{K}^{-1}:\mathcal{T}\to \mathcal{C}
cinemática inversa
especificación de la tarea
(se tiene)
referencias para los servos
(se quiere)
\mathbf{q}
\subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathcal{K}^{-1}:\mathcal{T}\to \mathcal{C}
cinemática inversa
especificación de la tarea
(se tiene)
referencias para los servos
(se quiere)
sin embargo, debemos entender antes cómo se mueve el robot
\mathbf{q}
\subseteq {^B}\mathbf{T}_E(\mathbf{q})
\mathcal{K}^{-1}:\mathcal{T}\to \mathcal{C}
cinemática inversa
especificación de la tarea
(se tiene)
referencias para los servos
(se quiere)
sin embargo, debemos entender antes cómo se mueve el robot
cinemática diferencial
La importancia de las velocidades
\mathbf{T}_d
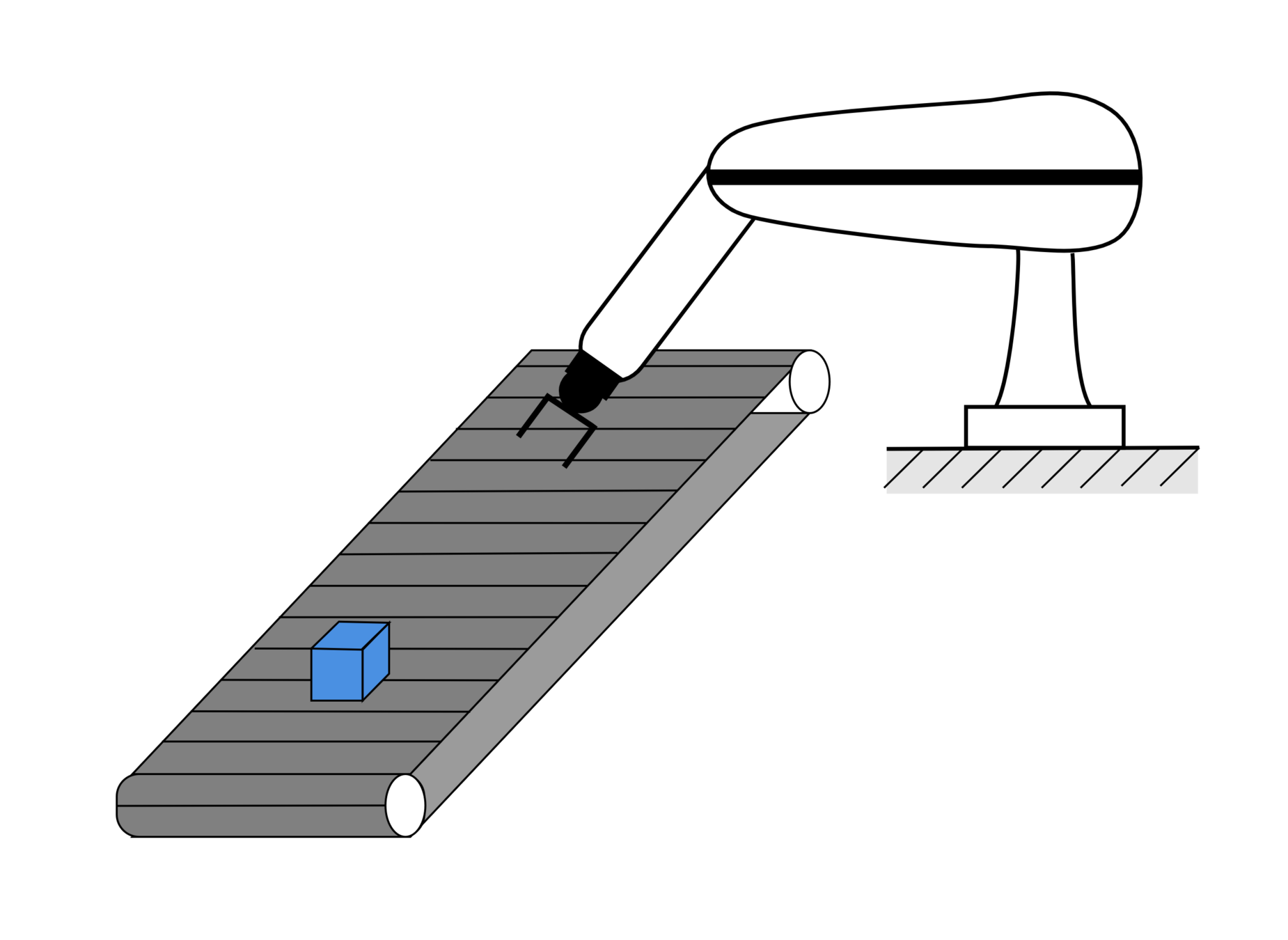
instante de tiempo \(t=t_1\)
La importancia de las velocidades
\mathbf{T}_d
instante de tiempo \(t=t_2\)
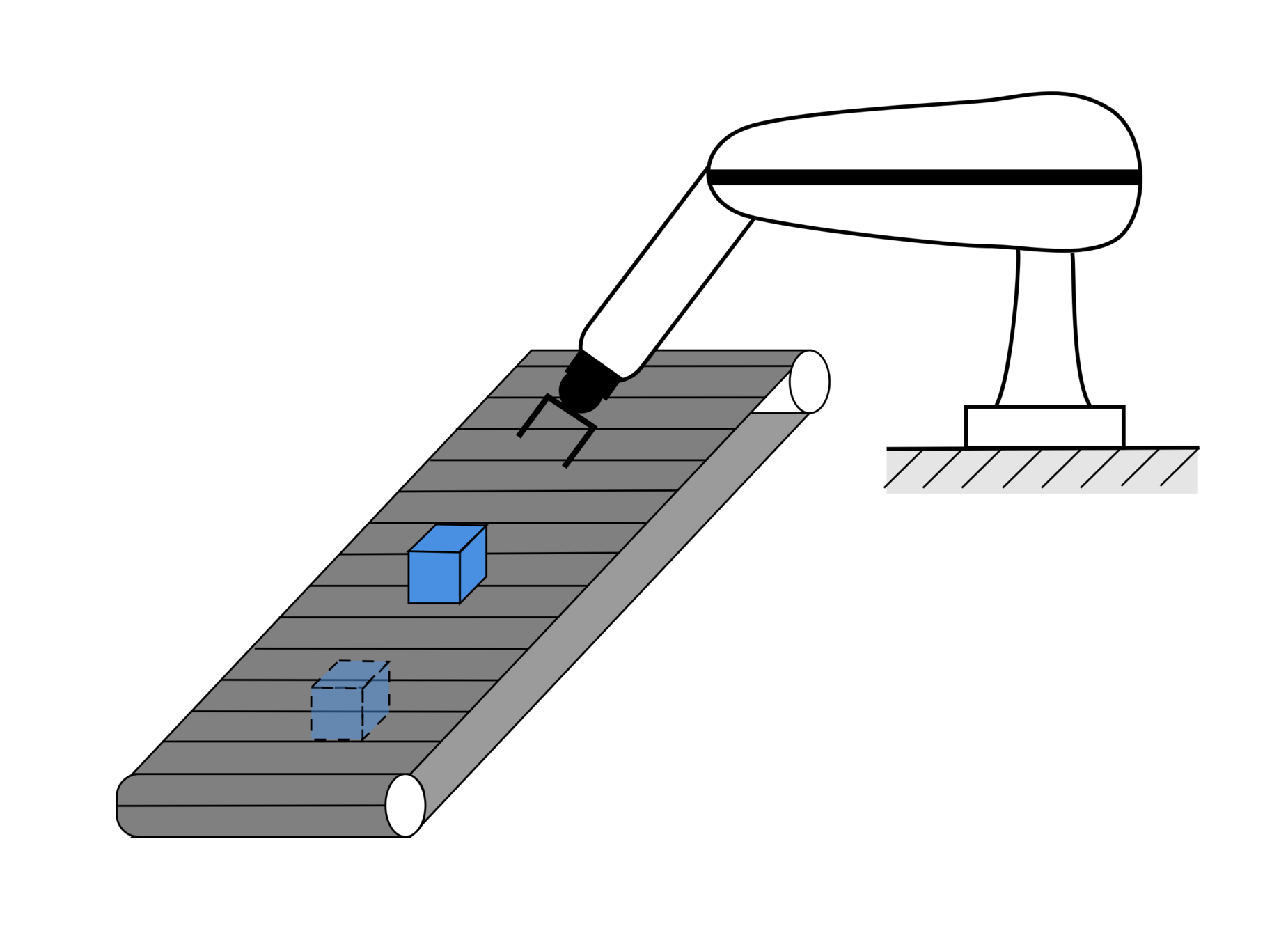
la tarea cambió en el tiempo
La importancia de las velocidades
\mathbf{T}_d
instante de tiempo \(t=t_2\)
la tarea cambió en el tiempo
¿Cómo hacemos que el robot tome en cuenta las velocidades?
\dot{\mathbf{q}}
{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}
\dot{\mathbf{q}}
{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}
{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}
cinemática diferencial
\mathbf{J}(\mathbf{q})=\dfrac{d\mathcal{K}(\mathbf{q})}{d\mathbf{q}} \in \mathbb{R}^{6 \times n}
la matriz
se conoce como el jacobiano del manipulador y mapea la velocidad de la configuración a la del efector final
\mathbf{J}(\mathbf{q})=\dfrac{d\mathcal{K}(\mathbf{q})}{d\mathbf{q}} \in \mathbb{R}^{6 \times n}
la matriz
se conoce como el jacobiano del manipulador y mapea la velocidad de la configuración a la del efector final
\mathbf{J}_v(\mathbf{q})=\dfrac{d{^B}\mathbf{o}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de posición o de velocidad lineal
(fácil)
{^B}\mathbf{J}(\mathbf{q})=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix}
\begin{matrix} \in\mathbb{R}^{3 \times n} \\ \in\mathbb{R}^{3 \times n} \end{matrix}
{^B}\mathbf{J}(\mathbf{q})=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix}
\begin{matrix} \in\mathbb{R}^{3 \times n} \\ \in\mathbb{R}^{3 \times n} \end{matrix}
\mathbf{J}_\omega(\mathbf{q})=\dfrac{d{^B}\boldsymbol{\theta}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de orientación o de velocidad angular
(difícil)
\mathbf{J}_v(\mathbf{q})=\dfrac{d{^B}\mathbf{o}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de posición o de velocidad lineal
(fácil)
{^B}\mathbf{J}(\mathbf{q})=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix}
\begin{matrix} \in\mathbb{R}^{3 \times n} \\ \in\mathbb{R}^{3 \times n} \end{matrix}
\mathbf{J}_\omega(\mathbf{q})=\dfrac{d{^B}\boldsymbol{\theta}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de orientación o de velocidad angular
(difícil)
\mathbf{J}_v(\mathbf{q})=\dfrac{d{^B}\mathbf{o}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de posición o de velocidad lineal
(fácil)
orientación abstracta
{^B}\mathbf{J}(\mathbf{q})=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix}
\begin{matrix} \in\mathbb{R}^{3 \times n} \\ \in\mathbb{R}^{3 \times n} \end{matrix}
\mathbf{J}_v(\mathbf{q})=\dfrac{d{^B}\mathbf{o}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de posición o de velocidad lineal
(fácil)
se omite cuando es respecto de la base
\mathbf{J}_\omega(\mathbf{q})=\dfrac{d{^B}\boldsymbol{\theta}_E(\mathbf{q})}{d\mathbf{q}}
jacobiano de orientación o de velocidad angular
(difícil)
orientación abstracta
\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix} \dot{\mathbf{q}}
similar a la cinemática directa, la cinemática diferencial también puede separarse en posición y orientación
\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix} \dot{\mathbf{q}}
similar a la cinemática directa, la cinemática diferencial también puede separarse en posición y orientación
velocidad lineal del efector final con respecto de la base
\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}=\begin{bmatrix} \mathbf{J}_v(\mathbf{q}) \\ \mathbf{J}_\omega(\mathbf{q}) \end{bmatrix} \dot{\mathbf{q}}
similar a la cinemática directa, la cinemática diferencial también puede separarse en posición y orientación
velocidad angular del efector final con respecto de la base, visto desde la base
\{A\}
\{B\}
\mathbf{p}(t_1)
\mathbf{p}(t_2)
{^A}\boldsymbol{\omega}_{AB} \text{ vs } {^A}\boldsymbol{\omega}_{BA} \text{ vs } {^B}\boldsymbol{\omega}_{AB}
{^A}\boldsymbol{\omega}_{AB}={^I}\mathbf{R}_B \ {^B}\boldsymbol{\omega}_{AB}
{^X}\boldsymbol{\omega}_{AB} = -{^X}\boldsymbol{\omega}_{BA}
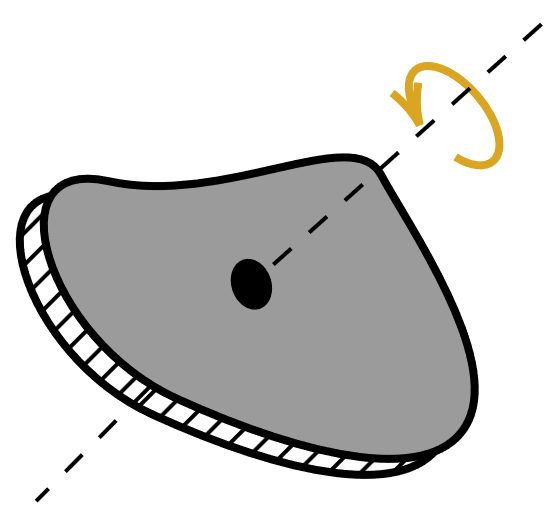
Recordatorio: velocidades angulares
Ejemplo: manipulador planar
\begin{array}{c|c|c|c}
\theta_j & d_j & a_j & \alpha_j \\ \hline
q_1 & 0 & a_1 & 0 \\ \hline
q_2 & 0 & a_2 & 0 \\
\end{array}
R
R
manipulador RR
{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\mathbf{J}(\mathbf{q})=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}
{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\mathbf{J}(\mathbf{q})=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}
\mathbf{J}_v(\mathbf{q})
\mathbf{J}_\omega(\mathbf{q})
{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\mathbf{J}(\mathbf{q})=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}
\mathbf{J}_v(\mathbf{q})
\mathbf{J}_\omega(\mathbf{q})
¿Cómo?
Consideraremos tres métodos
si extraemos la posición y orientación del efector final
Método 1: desde la definición
{^B}\mathbf{o}_E(\mathbf{q})={^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \\ z_E(\mathbf{q}) \end{bmatrix}=\begin{bmatrix} a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 \end{bmatrix}
{^B}\mathbf{R}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 \\ 0 & 0 & 1 \end{bmatrix}
podemos emplear la definición literal del jacobiano para obtener
\mathbf{J}_v(\mathbf{q})=\dfrac{d{^B}\mathbf{o}_E(\mathbf{q})}{d\mathbf{q}}=\begin{bmatrix} \frac{\partial x_E(\mathbf{q})}{\partial q_1} & \frac{\partial x_E(\mathbf{q})}{\partial q_2} \\
\frac{\partial y_E(\mathbf{q})}{\partial q_1} & \frac{\partial y_E(\mathbf{q})}{\partial q_2} \\
\frac{\partial z_E(\mathbf{q})}{\partial q_1} & \frac{\partial z_E(\mathbf{q})}{\partial q_2} \end{bmatrix}
\mathbf{J}_v(\mathbf{q})=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \end{bmatrix}
sin embargo, la situación se complica para la orientación
\mathbf{J}_\omega(\mathbf{q})=\dfrac{d{^B}\boldsymbol{\theta}_E(\mathbf{q})}{d\mathbf{q}}=
\begin{bmatrix} \frac{\partial \theta_1(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_1(\mathbf{q})}{\partial q_2} \\
\frac{\partial \theta_2(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_2(\mathbf{q})}{\partial q_2} \\
\frac{\partial \theta_3(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_3(\mathbf{q})}{\partial q_2} \end{bmatrix}
sin embargo, la situación se complica para la orientación
\mathbf{J}_\omega(\mathbf{q})=\dfrac{d{^B}\boldsymbol{\theta}_E(\mathbf{q})}{d\mathbf{q}}=
\begin{bmatrix} \frac{\partial \theta_1(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_1(\mathbf{q})}{\partial q_2} \\
\frac{\partial \theta_2(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_2(\mathbf{q})}{\partial q_2} \\
\frac{\partial \theta_3(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_3(\mathbf{q})}{\partial q_2} \end{bmatrix}
????
sin embargo, la situación se complica para la orientación
\mathbf{J}_\omega(\mathbf{q})=\dfrac{d{^B}\boldsymbol{\theta}_E(\mathbf{q})}{d\mathbf{q}}=
\begin{bmatrix} \frac{\partial \theta_1(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_1(\mathbf{q})}{\partial q_2} \\
\frac{\partial \theta_2(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_2(\mathbf{q})}{\partial q_2} \\
\frac{\partial \theta_3(\mathbf{q})}{\partial q_1} & \frac{\partial \theta_3(\mathbf{q})}{\partial q_2} \end{bmatrix}
recordemos que la orientación es una matriz y cambia según la representación seleccionada, por lo que el jacobiano no puede calcularse de forma "normal"
????
para calcularlo debe emplearse la relación
{^B}\dot{\mathbf{R}}_E {^B}\mathbf{R}_E^\top=\mathcal{S}\left({^B}\boldsymbol{\omega}_{BE}\right)
para calcularlo debe emplearse la relación
{^B}\dot{\mathbf{R}}_E {^B}\mathbf{R}_E^\top=\mathcal{S}\left({^B}\boldsymbol{\omega}_{BE}\right)
\mathcal{S}(\boldsymbol{\omega})=
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}
Sw = skew(w)
w = vex(Sw)para calcularlo debe emplearse la relación
{^B}\dot{\mathbf{R}}_E {^B}\mathbf{R}_E^\top=\mathcal{S}\left({^B}\boldsymbol{\omega}_{BE}\right)
{^B}\dot{\mathbf{R}}_E = \begin{bmatrix} -\sin(q_1+q_2)\left(\dot{q}_1+\dot{q}_2\right) & -\cos(q_1+q_2)\left(\dot{q}_1+\dot{q}_2\right) & 0 \\
\cos(q_1+q_2)\left(\dot{q}_1+\dot{q}_2\right) & -\sin(q_1+q_2)\left(\dot{q}_1+\dot{q}_2\right) & 0 \\ 0 & 0 & 0 \end{bmatrix}
entonces
{^B}\mathbf{R}_E^\top = \begin{bmatrix} \cos(q_1+q_2) & \sin(q_1+q_2) & 0 \\ -\sin(q_1+q_2) & \cos(q_1+q_2) & 0 \\ 0 & 0 & 1 \end{bmatrix}
\mathcal{S}\left({^B}\boldsymbol{\omega}_{BE}\right)={^B}\dot{\mathbf{R}}_E {^B}\mathbf{R}_E^\top=
\begin{bmatrix} 0 & -\dot{q}_1-\dot{q}_2 & 0 \\ \dot{q}_1+\dot{q}_2 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}
\mathcal{S}\left({^B}\boldsymbol{\omega}_{BE}\right)={^B}\dot{\mathbf{R}}_E {^B}\mathbf{R}_E^\top=
\begin{bmatrix} 0 & -\dot{q}_1-\dot{q}_2 & 0 \\ \dot{q}_1+\dot{q}_2 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}
{^B}\boldsymbol{\omega}_{BE}(\mathbf{q})=\begin{bmatrix} 0 \\ 0 \\ \dot{q}_1+\dot{q}_2 \end{bmatrix}
=\begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} \dot{q}_1 \\ \dot{q}_2 \end{bmatrix}
\omega_x
\omega_y
\omega_z
\mathcal{S}\left({^B}\boldsymbol{\omega}_{BE}\right)={^B}\dot{\mathbf{R}}_E {^B}\mathbf{R}_E^\top=
\begin{bmatrix} 0 & -\dot{q}_1-\dot{q}_2 & 0 \\ \dot{q}_1+\dot{q}_2 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}
{^B}\boldsymbol{\omega}_{BE}(\mathbf{q})=\begin{bmatrix} 0 \\ 0 \\ \dot{q}_1+\dot{q}_2 \end{bmatrix}
=\begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} \dot{q}_1 \\ \dot{q}_2 \end{bmatrix}
\omega_x
\omega_y
\omega_z
\mathbf{J}_\omega(\mathbf{q})
\dot{\mathbf{q}}
hay una fila del jacobiano asociada a cada uno de los GDL del efector final, recordar que \(\mathbf{J}(\mathbf{q})\in\mathbb{R}^{6\times n}\)
Consideraciones importantes
hay una fila del jacobiano asociada a cada uno de los GDL del efector final, recordar que \(\mathbf{J}(\mathbf{q})\in\mathbb{R}^{6\times n}\)
si \(\mathcal{K}\) no incluye todos los GDL del efector final, entonces para el jacobiano se toman sólo las filas relevantes
Consideraciones importantes
pueden emplearse tanto las herramientas que proveen MATLAB y la Robotics Toolbox
>> mt3005_clase6_jacobianoRR.mlx
o aproximar numéricamente las expresiones analíticas previas
\(\Rightarrow\) Laboratorio 7
Método 2: aproximaciones numéricas
pueden emplearse tanto las herramientas que proveen MATLAB y la Robotics Toolbox
>> mt3005_clase6_jacobianoRR.mlx
o aproximar numéricamente las expresiones analíticas previas
\(\Rightarrow\) Laboratorio 7
Método 2: aproximaciones numéricas
Siciliano et al.* presentan un método analítico alternativo con base en la convención DH
Método 3: alternativa analítica
\mathbf{J}(\mathbf{q})=\begin{bmatrix} \boldsymbol{\jmath}_{P_1} & \cdots & \boldsymbol{\jmath}_{P_n} \\
\boldsymbol{\jmath}_{O_1} & \cdots & \boldsymbol{\jmath}_{O_n} \end{bmatrix}
Siciliano et al.* presentan un método analítico alternativo con base en la convención DH
Método 3: alternativa analítica
\mathbf{J}(\mathbf{q})=\begin{bmatrix} \boldsymbol{\jmath}_{P_1} & \cdots & \boldsymbol{\jmath}_{P_n} \\
\boldsymbol{\jmath}_{O_1} & \cdots & \boldsymbol{\jmath}_{O_n} \end{bmatrix}
aporte de la \(n-\)ésima junta a los jacobianos de Posición y Orientación
Prismática
Método 3: alternativa analítica
\begin{bmatrix} \boldsymbol{\jmath}_{P_i} \\ \boldsymbol{\jmath}_{O_i} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_{i-1} \\ \mathbf{0} \end{bmatrix}
\begin{bmatrix} \boldsymbol{\jmath}_{P_i} \\ \boldsymbol{\jmath}_{O_i} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_{i-1} \times \left({^0}\mathbf{o}_E-{^0}\mathbf{p}_{i-1}\right) \\ {^0}\mathbf{z}_{i-1} \end{bmatrix}
Revoluta
Prismática
Método 3: alternativa analítica
\begin{bmatrix} \boldsymbol{\jmath}_{P_i} \\ \boldsymbol{\jmath}_{O_i} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_{i-1} \\ \mathbf{0} \end{bmatrix}
\begin{bmatrix} \boldsymbol{\jmath}_{P_i} \\ \boldsymbol{\jmath}_{O_i} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_{i-1} \times \left({^0}\mathbf{o}_E-{^0}\mathbf{p}_{i-1}\right) \\ {^0}\mathbf{z}_{i-1} \end{bmatrix}
Revoluta
eje de rotación o traslación asociado a la \(i-\)ésima junta
posición | origen del marco de la \(i-\)ésima junta
Método 3: alternativa analítica
{^0}\mathbf{z}_{i-1}={^0}\mathbf{R}_{i-1}\mathbf{z}_0={^0}\mathbf{R}_1(q_1) \cdots {^{i-2}}\mathbf{R}_{i-1}(q_{i-1})\mathbf{z}_0 \\
\mathbf{z}_0=\begin{bmatrix} 0 & 0 & 1 \end{bmatrix}^\top
{^0}\mathbf{p}_{i-1}={^0}\mathbf{T}_{i-1}\tilde{\mathbf{p}}_0=\mathbf{A}_1(q_1) \cdots \mathbf{A}_{i-1}(q_{i-1})\tilde{\mathbf{p}}_0 \\
\tilde{\mathbf{p}}_0=\begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}^\top
Método 3: alternativa analítica
{^0}\mathbf{z}_{i-1}={^0}\mathbf{R}_{i-1}\mathbf{z}_0={^0}\mathbf{R}_1(q_1) \cdots {^{i-2}}\mathbf{R}_{i-1}(q_{i-1})\mathbf{z}_0 \\
\mathbf{z}_0=\begin{bmatrix} 0 & 0 & 1 \end{bmatrix}^\top
\(i=1,2,...,n\)
\(\{0\}=\{B\}\) (típicamente)
{^0}\mathbf{p}_{i-1}={^0}\mathbf{T}_{i-1}\tilde{\mathbf{p}}_0=\mathbf{A}_1(q_1) \cdots \mathbf{A}_{i-1}(q_{i-1})\tilde{\mathbf{p}}_0 \\
\tilde{\mathbf{p}}_0=\begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}^\top
Continuando el ejemplo
\begin{array}{c|c|c|c}
\theta_j & d_j & a_j & \alpha_j \\ \hline
q_1 & 0 & a_1 & 0 \\ \hline
q_2 & 0 & a_2 & 0 \\
\end{array}
R
R
manipulador RR
{^0}\mathbf{T}_0=\mathbf{I}=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^0}\mathbf{T}_0=\mathbf{I}=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^0}\mathbf{z}_0
{^0}\mathbf{p}_0
{^0}\mathbf{T}_1=\begin{bmatrix} \cos(q_1) & -\sin(q_1) & 0 & a_1\cos(q_1) \\
\sin(q_1) & \cos(q_1) & 0 & a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^0}\mathbf{T}_1=\mathbf{A}_1(q_1)=\mathbf{T}_{r_z}(q_1)\mathbf{T}_z(0)\mathbf{T}_x(a_1)\mathbf{T}_{r_x}(0)
{^0}\mathbf{T}_1=\begin{bmatrix} \cos(q_1) & -\sin(q_1) & 0 & a_1\cos(q_1) \\
\sin(q_1) & \cos(q_1) & 0 & a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^0}\mathbf{T}_1=\mathbf{A}_1(q_1)=\mathbf{T}_{r_z}(q_1)\mathbf{T}_z(0)\mathbf{T}_x(a_1)\mathbf{T}_{r_x}(0)
{^0}\mathbf{z}_1
{^0}\mathbf{p}_1
{^0}\mathbf{T}_2=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\
\sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^0}\mathbf{T}_2=\mathbf{A}_1(q_1)\mathbf{A}_2(q_2)=\mathbf{A}_1(q_1)\mathbf{T}_{r_z}(q_2)\mathbf{T}_z(0)\mathbf{T}_x(a_2)\mathbf{T}_{r_x}(0)
{^0}\mathbf{T}_2=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\
\sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^0}\mathbf{T}_2=\mathbf{A}_1(q_1)\mathbf{A}_2(q_2)=\mathbf{A}_1(q_1)\mathbf{T}_{r_z}(q_2)\mathbf{T}_z(0)\mathbf{T}_x(a_2)\mathbf{T}_{r_x}(0)
{^0}\mathbf{o}_E
\begin{bmatrix} \boldsymbol{\jmath}_{P_1} \\ \boldsymbol{\jmath}_{O_1} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_0 \times \left({^0}\mathbf{o}_E-{^0}\mathbf{p}_0\right) \\ {^0}\mathbf{z}_0 \end{bmatrix}=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1+q_2) \\ a_1\cos(q_1)+a_2\cos(q_1+q_2) \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}
\begin{bmatrix} \boldsymbol{\jmath}_{P_2} \\ \boldsymbol{\jmath}_{O_2} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_1 \times \left({^0}\mathbf{o}_E-{^0}\mathbf{p}_1\right) \\ {^0}\mathbf{z}_1 \end{bmatrix}=
\begin{bmatrix} -a_2\sin(q_1+q_2) \\ a_2\cos(q_1+q_2) \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}
\begin{bmatrix} \boldsymbol{\jmath}_{P_1} \\ \boldsymbol{\jmath}_{O_1} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_0 \times \left({^0}\mathbf{o}_E-{^0}\mathbf{p}_0\right) \\ {^0}\mathbf{z}_0 \end{bmatrix}=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1+q_2) \\ a_1\cos(q_1)+a_2\cos(q_1+q_2) \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}
\begin{bmatrix} \boldsymbol{\jmath}_{P_2} \\ \boldsymbol{\jmath}_{O_2} \end{bmatrix}=
\begin{bmatrix} {^0}\mathbf{z}_1 \times \left({^0}\mathbf{o}_E-{^0}\mathbf{p}_1\right) \\ {^0}\mathbf{z}_1 \end{bmatrix}=
\begin{bmatrix} -a_2\sin(q_1+q_2) \\ a_2\cos(q_1+q_2) \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}
\mathbf{J}(\mathbf{q})=\begin{bmatrix} \boldsymbol{\jmath}_{P_1} & \boldsymbol{\jmath}_{P_2} \\
\boldsymbol{\jmath}_{O_1} & \boldsymbol{\jmath}_{O_2} \end{bmatrix}=
\begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}
Cambiando el marco del jacobiano
en caso de necesitar referenciar al jacobiano con respecto de otro marco de referencia \(\{D\}\) en lugar de la base, puede emplearse la transformación
{^D}\mathbf{J}(\mathbf{q})=\begin{bmatrix} {^B}\mathbf{R}_D^\top & \mathbf{0} \\ \mathbf{0} & {^B}\mathbf{R}_D^\top \end{bmatrix} \mathbf{J}(\mathbf{q})
MT3005 - Lecture 6 (2025)
By Miguel Enrique Zea Arenales
