Introducción a la planificación de movimiento

MT3005 - Robótica 1

¿Por qué?

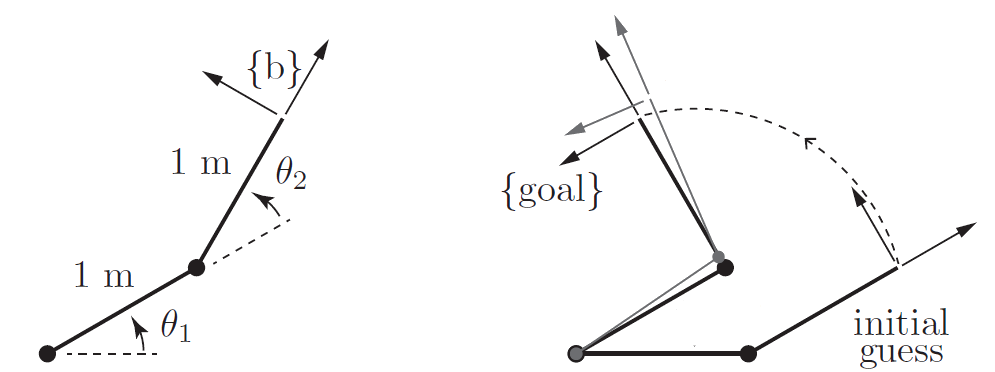
Control cinemático puro


Control cinemático puro


¿Obstáculos?
\(\Rightarrow\) por esto necesitamos al planificador | generador de trayectorias en el esquema de control jerárquico por capas


¿Obstáculos?
si bien no profundizaremos al respecto, veamos algunas de las ideas y métodos detrás de la planificación de movimiento


¿Obstáculos?
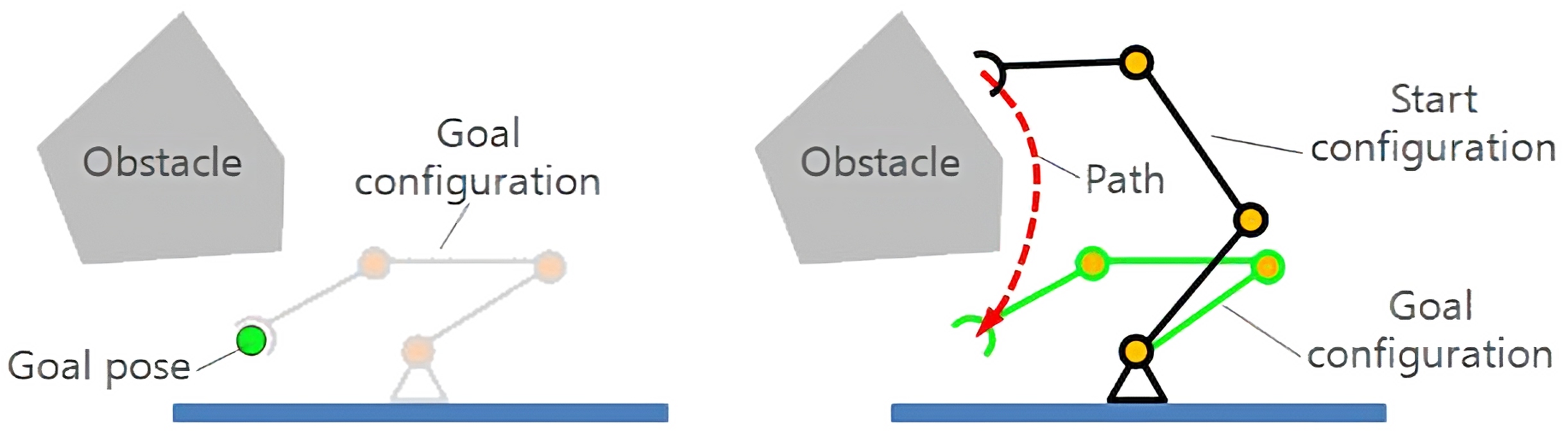
Dos problemas similares

Dos problemas similares


¿Cuál es la diferencia?
Dos problemas similares


¿Cuál es la diferencia?
Dos problemas similares
\(\Rightarrow\) el espacio de configuración

Espacio de configuración para brazos
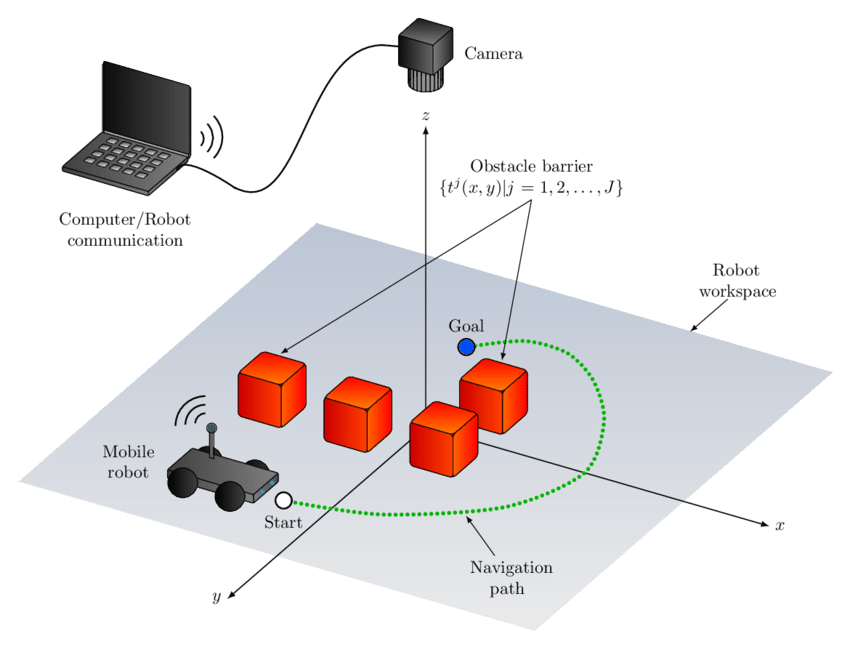
Espacio de configuración para robots móviles


Espacio de configuración para robots móviles

Espacio de configuración para robots móviles

Espacio de configuración para robots móviles
occupancy grid
- Métodos de búsqueda en grafos
- algoritmo de Dijkstra
- variantes como A* | D* | etc.
- Métodos de muestreo
- rapidly exploring random trees (RRT)
- probabilistic roadmaps (PRM)
- Virtual potential fields
- Optimización no lineal (Control 2)
Métodos de planificación de movimiento
- Métodos de búsqueda en grafos
- algoritmo de Dijkstra
- variantes como A* | D* | etc.
- Métodos de muestreo
- rapidly exploring random trees (RRT)
- probabilistic roadmaps (PRM)
- Virtual potential fields
- Optimización no lineal (Control 2)
Métodos de planificación de movimiento

Rapidly Exploring Random Trees (RRT)
Entrada:
punto inicial y meta en el espacio de configuración
Salida:
recorrido de inicio a meta
Rapidly Exploring Random Trees (RRT)
Algoritmo:
- Insertar el(los) punto(s) inicial(es) en el(los) árbol(es).
- Mientras que el árbol no pueda conectarse a la meta:
- Muestree un punto aleatorio \(r\) en el espacio de configuración.
- Encuentre el punto \(p\) en el árbol que esté más cercano a \(r\).
- Añada una rama de un largo predeterminado a \(p\), en la dirección de \(r\).
- Si la nueva rama interseca un obstáculo:
- Descarte la nueva rama (o acórtela).
- Calcule el recorrido desde el punto de inicio hasta la meta a través del árbol.
- Atajos en el recorrido: para cualquiera dos puntos en el recorrido, añada una línea directa entre ellos a menos que esta interseque un obstáculo.
Ejemplo RRT

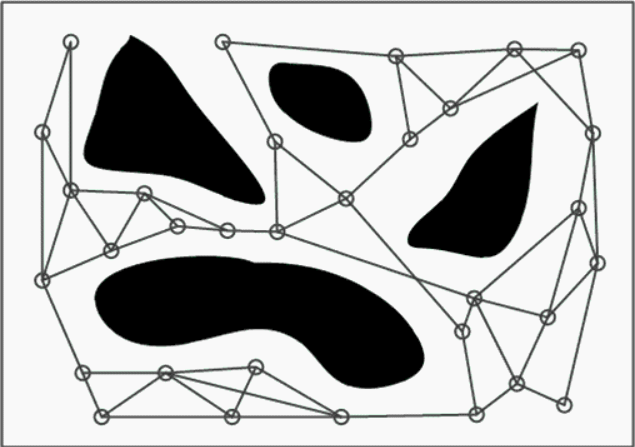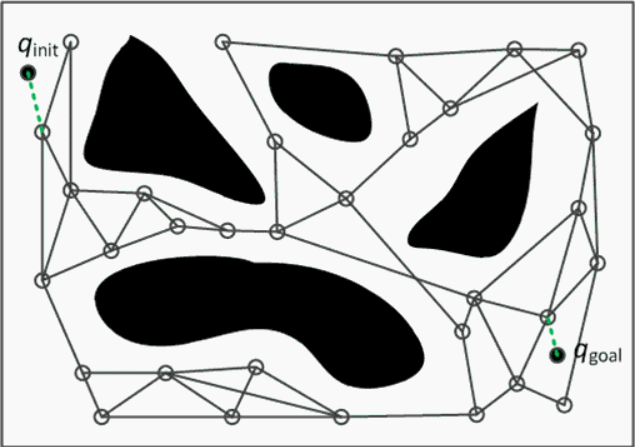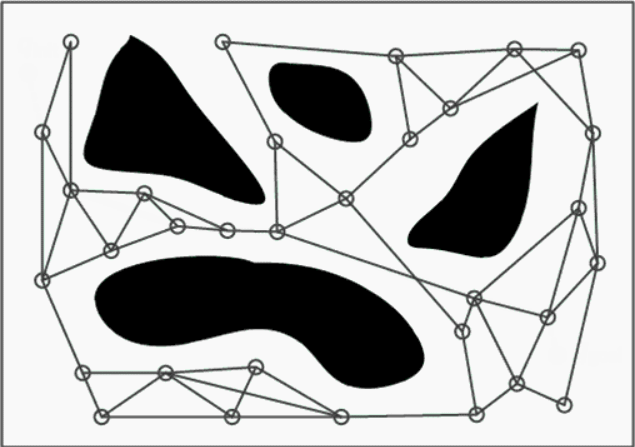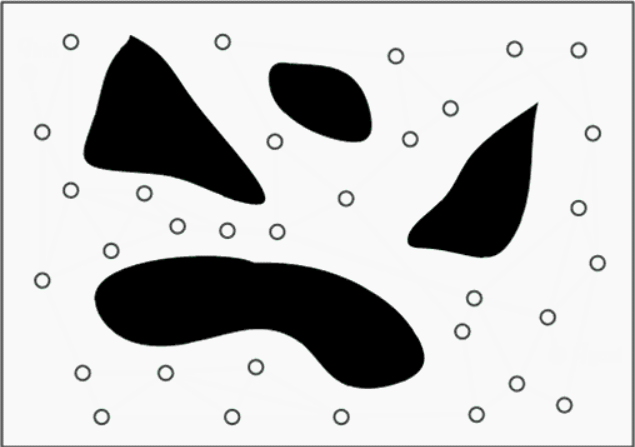
Probabilistic Roadmaps (PRM)
Probabilistic Roadmaps (PRM)
Entrada:
punto inicial y meta en el espacio de configuración
Salida:
recorrido de inicio a meta
Construcción del mapa:
- Mientras que el número de puntos en el mapa sea menor que cierto valor de umbral:
- Muestree un punto aleatorio en el espacio de configuración.
- Si el nuevo punto no se encuentra en colisión:
- Conecte el nuevo punto a todos los puntos en el mapa mediante líneas, siempre y cuando éstas no intersequen obstáculos.
Probabilistic Roadmaps (PRM)
Encontrar recorrido:
- Conecte el punto de inicio al punto más cercano en el mapa tal que la línea que los conecta no interseque obstáculos.
- Conecte la meta al punto más cercano en el mapa tal que la línea que los conecta no interseque obstáculos.
- Encuentre un recorrido que vaya desde el inicio hasta la meta exclusivamente dentro del mapa.
Probabilistic Roadmaps (PRM)
Ejemplo PRM

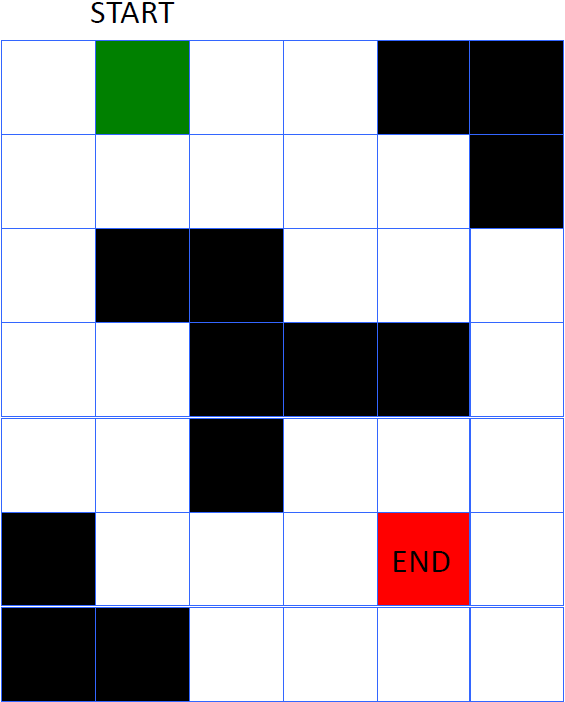
Métodos de búsqueda en grafos


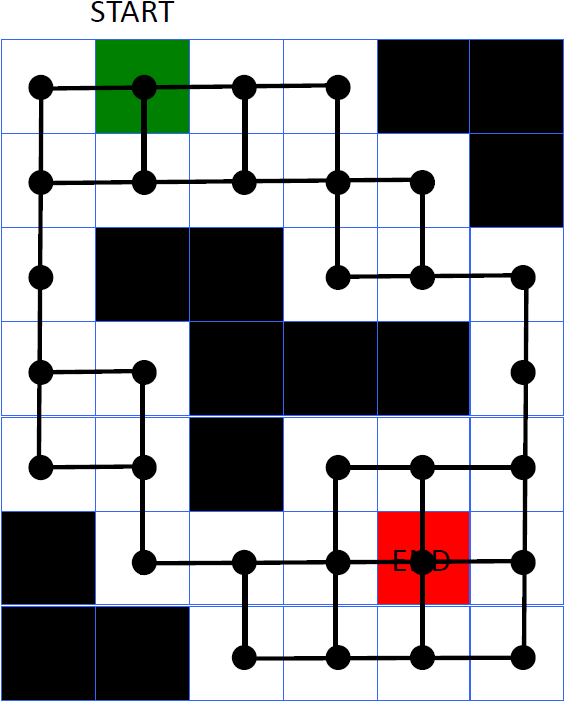
Métodos de búsqueda en grafos
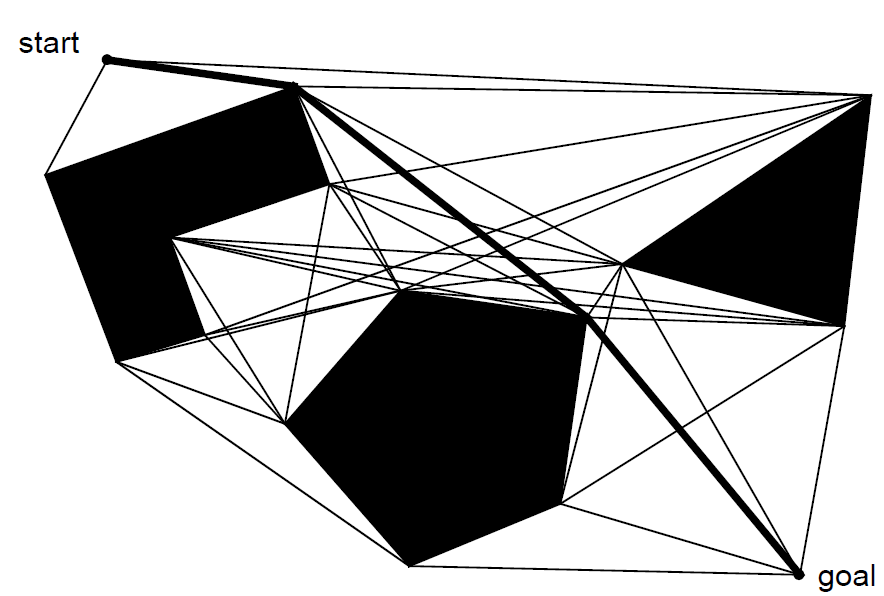
De mapas a grafos | grafo de visibilidad
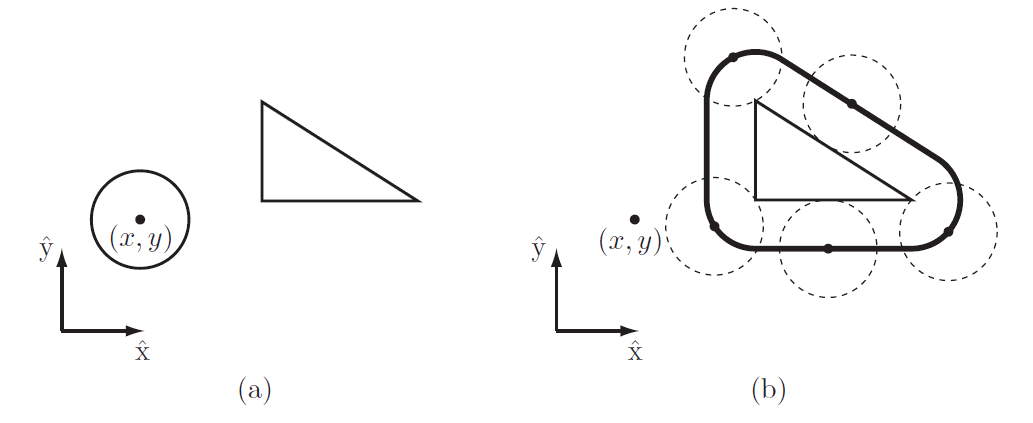

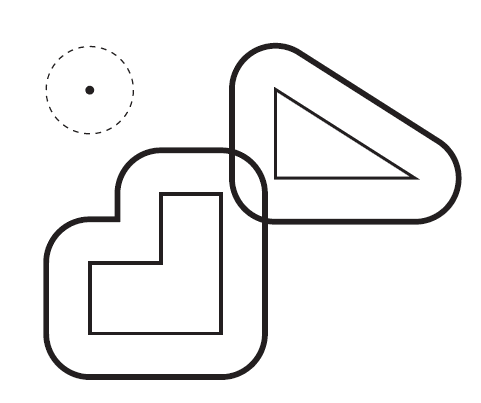
Aumento de mapa



Aumento de mapa



Aumento de mapa
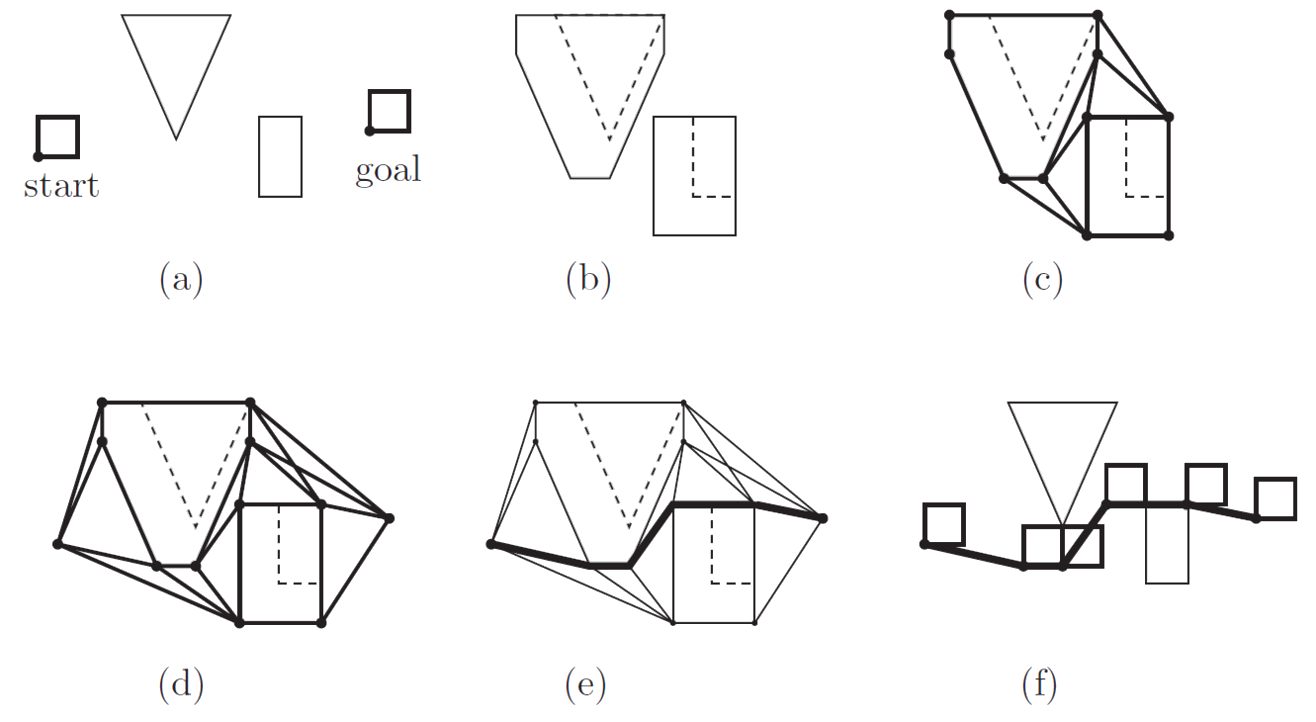
Procedimiento
Para cada nodo \(n\), matiene un registro del tamaño del camino más corto desde el inicio a \(n\), encontrado hasta el momento, llamado \(g(n)\).
El algoritmo de Dijkstra
Entradas:
grafo de visibilidad, inicio \(S\) y meta \(G\)
Salida:
recorrido de \(S\) a \(G\)
Algoritmo:
- Etiquete a todos los nodos como "no visitados".
- Marque \(S\) para que tenga \(g(S)=0\).
- Mientras que existan nodos sin visitar:
- Escoja el nodo sin visitar con el menor \(g(n)\).
- Etiquete \(n\) como visitado.
-
Para cada vecino \(r\) de \(n\):
- \(g(r)=\min\{g(r), g(n)+d(n,r)\}\).
- Asigne de qué vecino proviene \(g(r)\).
El algoritmo de Dijkstra


El algoritmo de Dijkstra
Ejemplo Dijkstra
Ejemplo Dijkstra
Ejemplo Dijkstra
Ejemplo Dijkstra
Ejemplo Dijkstra
- Para cada nodo \(n\), se utiliza adicionalmente una heurística que estima qué tan lejos está \(n\) de la meta, llamada \(h(n)\).
- Una heurística es admisible sólo si nunca sobreestima la distancia real. Una empleada usualmente (que cumple con el requerimiento) es la distancia entre dos puntos.
Búsqueda A* | Dijkstra + heurística
Búsqueda A* | Dijkstra + heurística
Entrada:
grafo de visibilidad, inicio \(S\) y meta \(G\)
Salida:
recorrido de \(S\) a \(G\)
Algoritmo:
- Etiquete a todos los nodos como "no visitados".
- Marque \(S\) para que tenga \(g(S)=0\), \(f(S)=g(S)+\)\(h(S)\).
- Mientras que existan nodos sin visitar:
- Escoja el nodo sin visitar con el menor \(f(n)\).
- Etiquete \(n\) como visitado.
- Para cada vecino \(r\) de \(n\):
- \(g(r)=\min\{g(r), g(n)+d(n,r)\}\).
- \(f(r)=g(r)+h(r)\).
Búsqueda A* | Dijkstra + heurística

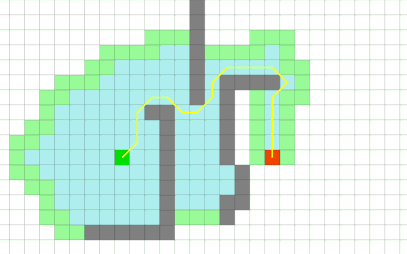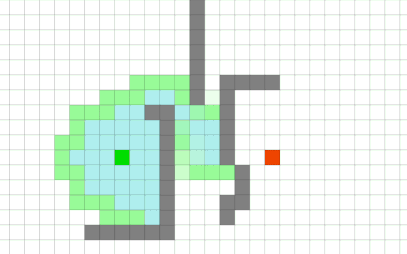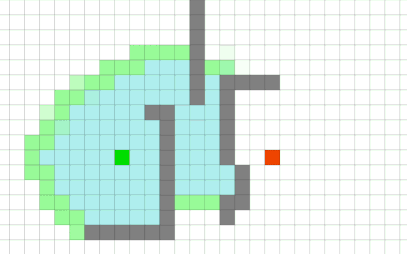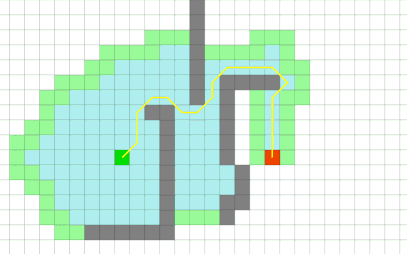

Búsqueda A* | Dijkstra + heurística
MT3005 - Lecture 14 (2025)
By Miguel Enrique Zea Arenales
MT3005 - Lecture 14 (2025)
- 100



