Modelado de robots móviles con ruedas

MT3005 - Robótica 1

Un tipo "simple" de robots de base móvil

hasta el momento hemos sido capaces de considerar una perspectiva puramente cinemática para el control de manipuladores
hasta el momento hemos sido capaces de considerar una perspectiva puramente cinemática para el control de manipuladores
desafortunadamente, las técnicas más avanzadas para controlar los mismos (y robots de base flotante) requieren de dinámica de cuerpos rígidos
hasta el momento hemos sido capaces de considerar una perspectiva puramente cinemática para el control de manipuladores
desafortunadamente, las técnicas más avanzadas para controlar los mismos (y robots de base flotante) requieren de dinámica de cuerpos rígidos
sin embargo, existe un tipo particular de robots de base móvil que sí pueden describirse y controlarse sólo con su cinemática





Robots móviles con ruedas
para la gran mayoría de aplicaciones (de robótica móvil) las ruedas son la solución más apropiada
para la gran mayoría de aplicaciones (de robótica móvil) las ruedas son la solución más apropiada
con tres ruedas se garantiza estabilidad (más de tres requieren de suspensión)
para la gran mayoría de aplicaciones (de robótica móvil) las ruedas son la solución más apropiada
con tres ruedas se garantiza estabilidad (más de tres requieren de suspensión)
la selección de ruedas depende de la aplicación
Tipos de ruedas
standard wheel
(2 DOF)

Tipos de ruedas
Tipos de ruedas
standard wheel
(2 DOF)
caster wheel
(3 DOF)


Tipos de ruedas
Tipos de ruedas
standard wheel
(2 DOF)
caster wheel
(3 DOF)
Swedish wheel
(3DOF)



Tipos de ruedas
Manipuladores vs robots con ruedas
movimiento de manipuladores definido por juntas actuadas
Manipuladores vs robots con ruedas
Manipuladores vs robots con ruedas
movimiento de manipuladores definido por juntas actuadas
movimiento de robot con ruedas definido por restricciones de rodamiento y no deslizamiento
Manipuladores vs robots con ruedas
Manipuladores vs robots con ruedas
movimiento de manipuladores definido por juntas actuadas
movimiento de robot con ruedas definido por restricciones de rodamiento y no deslizamiento
en ambos nos interesa la cinemática directa e inversa, sin embargo, para los robots con ruedas los valores de los encoders no pueden mapearse a poses únicas
Manipuladores vs robots con ruedas
Manipuladores vs robots con ruedas
movimiento de manipuladores definido por juntas actuadas
movimiento de robot con ruedas definido por restricciones de rodamiento y no deslizamiento
en ambos nos interesa la cinemática directa e inversa, sin embargo, para los robots con ruedas los valores de los encoders no pueden mapearse a poses únicas
Manipuladores vs robots con ruedas
\(\Rightarrow\) no hay forma instantánea de medir su posición




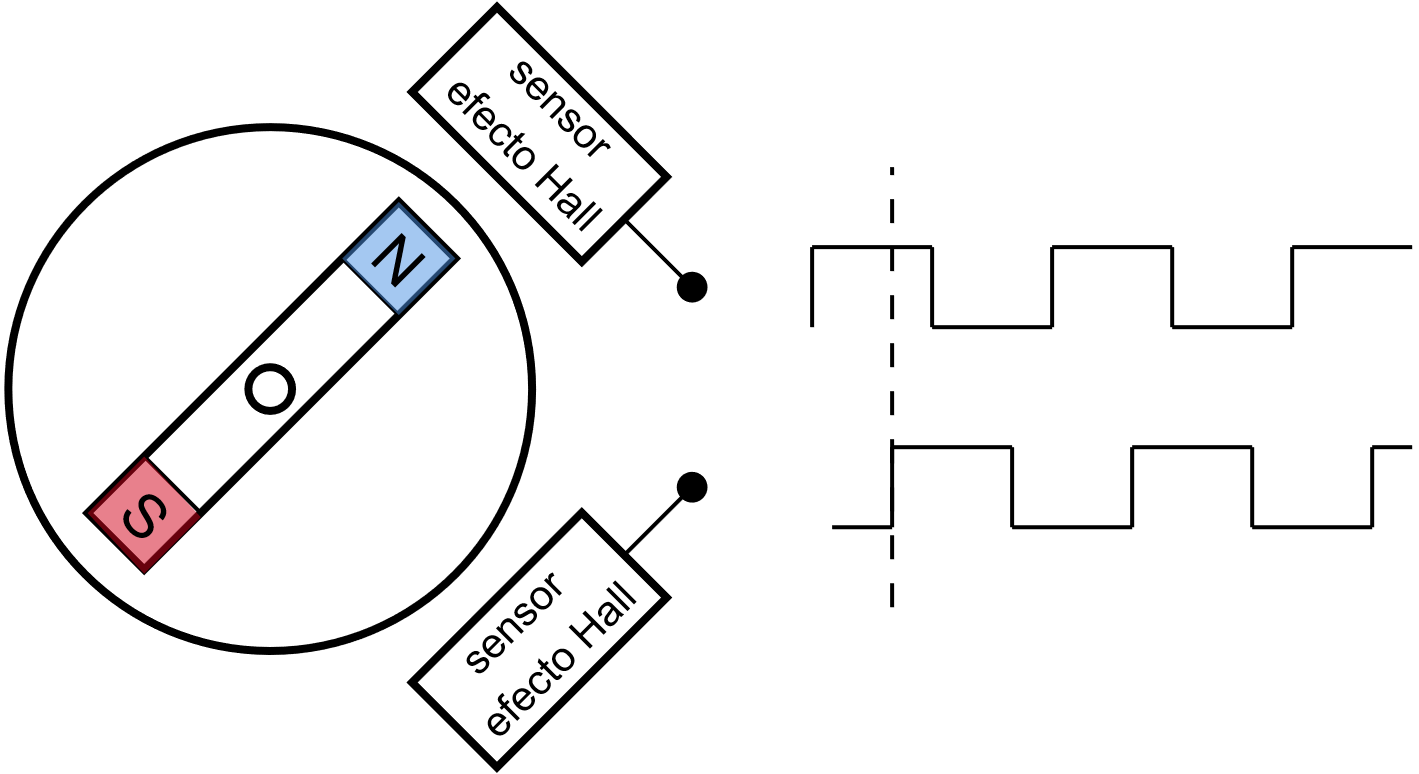



ej. encoder magnético



ej. encoder magnético
NO aplica para robots con ruedas
Sistemas no holonómicos
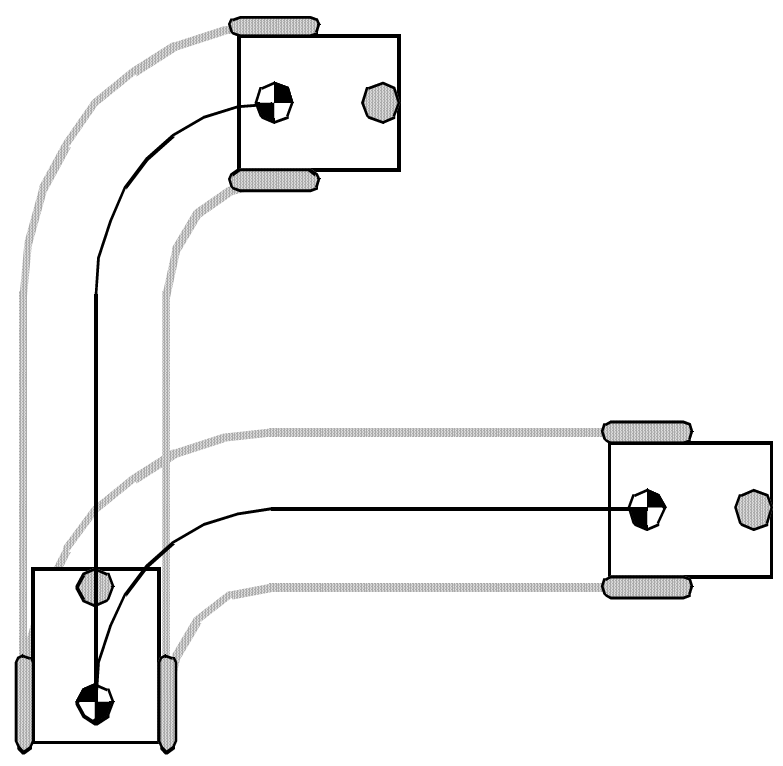
\(s=r\varphi\) distancia recorrida
Sistemas no holonómicos

\(s=r\varphi\) distancia recorrida
Sistemas no holonómicos

\(s=r\varphi\) distancia recorrida
Sistemas no holonómicos
en el caso de robots con ruedas se tiene entonces un set de restricciones no integrables
(restricciones no holonómicas)
en el caso de robots con ruedas se tiene entonces un set de restricciones no integrables
(restricciones no holonómicas)
por lo tanto, si tenemos restricciones de velocidad pero nos interesa la cinemática del robot
\(\Rightarrow\) cinemática diferencial
+
Cinemática diferencial: rueda estándar fija
chasis del robot
+
Cinemática diferencial: rueda estándar fija
chasis del robot
+
Cinemática diferencial: rueda estándar fija
chasis del robot
+
\(\beta \to \beta(t)\) para una caster wheel
Cinemática diferencial: rueda estándar fija
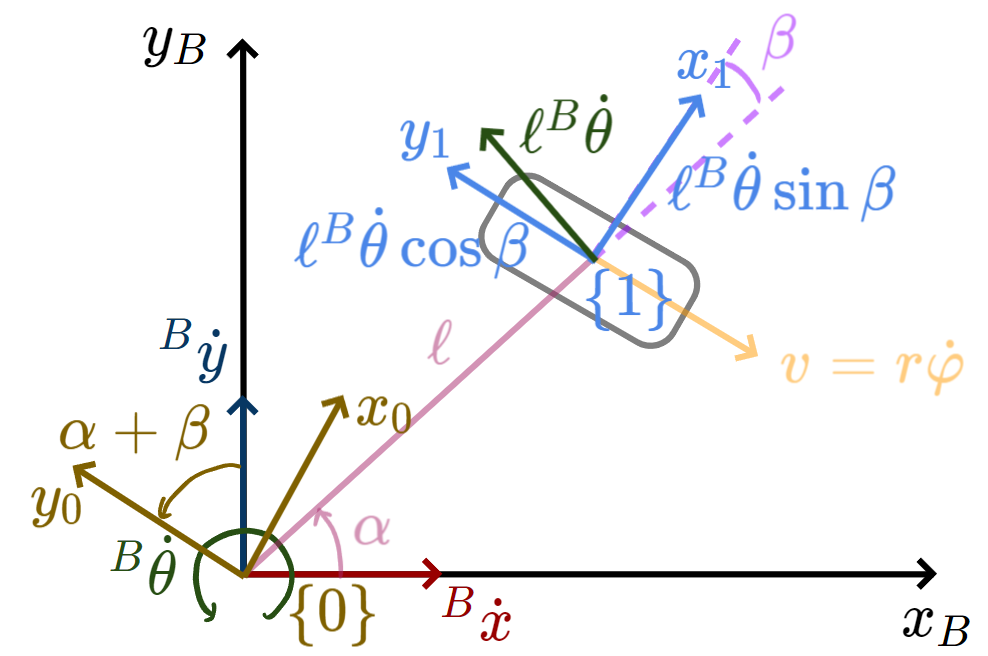
velocidad de la rueda, desde el marco de la rueda

velocidad de la rueda, desde el marco de la rueda
restricción de no deslizamiento
restricción de rodamiento

velocidad de la rueda, desde el marco de la rueda
restricción de no deslizamiento
restricción de rodamiento
la velocidad de la rueda es la combinación de todas las velocidades que experimenta el robot
Rodamiento:
Rodamiento:
Rodamiento:
Rodamiento:
¿Por qué?
Rodamiento:
¿Por qué?
es el equivalente de la configuración pero para robots con ruedas
No deslizamiento:
No deslizamiento:
No deslizamiento:
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
velocidad de las ruedas
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
velocidad de las ruedas
para obtener el modelo del robot, se apilan las restricciones de cada rueda (asumiendo \(N\) ruedas):
velocidad de las ruedas
velocidad del robot
Ejemplo: robot diferencial (differential drive)
Ejemplo: robot diferencial (differential drive)
Ejemplo: robot diferencial (differential drive)
Ejemplo: robot diferencial (differential drive)
>> mt3005_clase12_modelado_diffdrive.mlx
>> mt3005_clase12_diffdrive.m
MT3005 - Lecture 12 (2025)
By Miguel Enrique Zea Arenales
MT3005 - Lecture 12 (2025)
- 122



