Generación de trayectorias
MT3005 - Robótica 1
paths (caminos | recorridos)
vs
trajectories (trayectorias)
Trayectoria = camino + especificación de tiempo
Trayectoria = camino + especificación de tiempo
conjunto de puntos ordenados en el espacio (\(\mathcal{C}\) o \(\mathcal{T}\)) que el robot debe seguir (puramente geométrico)
Trayectoria = camino + especificación de tiempo
conjunto de puntos ordenados en el espacio (\(\mathcal{C}\) o \(\mathcal{T}\)) que el robot debe seguir (puramente geométrico)
qué tan rápido ejecutará el robot el camino (acorde a los límites de los actuadores)
Trayectoria = camino + especificación de tiempo
conjunto de puntos ordenados en el espacio (\(\mathcal{C}\) o \(\mathcal{T}\)) que el robot debe seguir (puramente geométrico)
qué tan rápido ejecutará el robot el camino (acorde a los límites de los actuadores)
velocidades
aceleraciones
Trayectoria = camino + especificación de tiempo
\mathbf{q}(s), \ s \in [0,1]
s(t), \ t \in [0,T]
Trayectoria = camino + especificación de tiempo
\mathbf{q}(s), \ s \in [0,1]
s(t), \ t \in [0,T]
\dot{\mathbf{q}}=\dfrac{d \mathbf{q}}{ds}\dot{s} \\
\ddot{\mathbf{q}}=\dfrac{d \mathbf{q}}{ds}\ddot{s}+\dfrac{d^2 \mathbf{q}}{ds^2}\dot{s}^2
Trayectoria = camino + especificación de tiempo
\mathbf{q}(s), \ s \in [0,1]
s(t), \ t \in [0,T]
\dot{\mathbf{q}}=\dfrac{d \mathbf{q}}{ds}\dot{s} \\
\ddot{\mathbf{q}}=\dfrac{d \mathbf{q}}{ds}\ddot{s}+\dfrac{d^2 \mathbf{q}}{ds^2}\dot{s}^2
por lo tanto, para garantizar la continuidad en la aceleración del robot, tanto el camino como la especificación de tiempo deben ser por lo menos dos veces diferenciables
Trayectoria = camino + especificación de tiempo
\mathbf{q}(s), \ s \in [0,1]
s(t), \ t \in [0,T]
\dot{\mathbf{q}}=\dfrac{d \mathbf{q}}{ds}\dot{s} \\
\ddot{\mathbf{q}}=\dfrac{d \mathbf{q}}{ds}\ddot{s}+\dfrac{d^2 \mathbf{q}}{ds^2}\dot{s}^2
por lo tanto, para garantizar la continuidad en la aceleración del robot, tanto el camino como la especificación de tiempo deben ser por lo menos dos veces diferenciables
las generaremos según la aplicación
Trayectorias punto a punto
se especifica la configuración | pose del efector final en los puntos inicial y final
se especifica la configuración | pose del efector final en los puntos inicial y final
NO nos importa* qué ocurre con la pose del efector durante la trayectoria
se especifica la configuración | pose del efector final en los puntos inicial y final
NO nos importa* qué ocurre con la pose del efector durante la trayectoria
Ejemplo: pick and place
\mathbf{T}_0
\mathbf{T}_f
\mathbf{T}_0
\mathbf{T}_f
\xrightarrow{\mathcal{K}^{-1}} \mathbf{q}_0
\xrightarrow{\mathcal{K}^{-1}} \mathbf{q}_f
\mathbf{T}_0
\mathbf{T}_f
\xrightarrow{\mathcal{K}^{-1}} \mathbf{q}_0
\xrightarrow{\mathcal{K}^{-1}} \mathbf{q}_f
interpolación en \(\mathcal{C}\)
Interpolación en \(\mathcal{C}\)
\mathbf{q}(s)=(1-s)\mathbf{q}_0+s\mathbf{q}_f
Interpolación en \(\mathcal{C}\)
\mathbf{q}(s)=(1-s)\mathbf{q}_0+s\mathbf{q}_f
(interpolación lineal)
Interpolación en \(\mathcal{C}\)
\mathbf{q}(s)=(1-s)\mathbf{q}_0+s\mathbf{q}_f
(interpolación lineal)
¿Escalamiento?
Interpolación en \(\mathcal{C}\)
\mathbf{q}(s)=(1-s)\mathbf{q}_0+s\mathbf{q}_f
(interpolación lineal)
¿Escalamiento? para garantizar una aceleración continua se requiere por lo menos un polinomio de 3er orden
Interpolación en \(\mathcal{C}\)
¿Escalamiento? para garantizar una aceleración continua se requiere por lo menos un polinomio de 3er orden
\mathbf{q}(s)=(1-s)\mathbf{q}_0+s\mathbf{q}_f
(interpolación lineal)
los más comunes:
- polinomios de 5to orden
- perfiles trapezoidales
- entre otros...
Polinomios de 5to orden
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
Polinomios de 5to orden
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
6 parámetros, permiten establecer condiciones en las posiciones, velocidades y aceleraciones inicial y final
Polinomios de 5to orden
\begin{array}{c|c|c|c}
t & s & \dot{s} & \ddot{s} \\ \hline
0 & s_0=0 & \dot{s}_0=0 & \ddot{s}_0=0 \\ \hline
T & s_T=1 & \dot{s}_T=0 & \ddot{s}_T=0 \\
\end{array}
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
Polinomios de 5to orden
\begin{array}{c|c|c|c}
t & s & \dot{s} & \ddot{s} \\ \hline
0 & s_0=0 & \dot{s}_0=0 & \ddot{s}_0=0 \\ \hline
T & s_T=1 & \dot{s}_T=0 & \ddot{s}_T=0 \\
\end{array}
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
interpolación
Polinomios de 5to orden
\begin{array}{c|c|c|c}
t & s & \dot{s} & \ddot{s} \\ \hline
0 & s_0=0 & \dot{s}_0=0 & \ddot{s}_0=0 \\ \hline
T & s_T=1 & \dot{s}_T=0 & \ddot{s}_T=0 \\
\end{array}
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
aceleración continua (velocidad suave)
Polinomios de 5to orden
\begin{array}{c|c|c|c}
t & s & \dot{s} & \ddot{s} \\ \hline
0 & s_0=0 & \dot{s}_0=0 & \ddot{s}_0=0 \\ \hline
T & s_T=1 & \dot{s}_T=0 & \ddot{s}_T=0 \\
\end{array}
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
jerk continuo (aceleración suave)
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
\dot{s}(t)=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4
\ddot{s}(t)=2a_2+6a_3t+12a_4t^2+20a_5t^3
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
\dot{s}(t)=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4
\ddot{s}(t)=2a_2+6a_3t+12a_4t^2+20a_5t^3
s(0)=s_0=a_0=0 \\
\dot{s}(0)=\dot{s}_0=a_1=0 \\
\ddot{s}(0)=\ddot{s}_0=2a_2=0
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
\dot{s}(t)=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4
\ddot{s}(t)=2a_2+6a_3t+12a_4t^2+20a_5t^3
s(T)=s_T=a_0+a_1T+a_2T^2+a_3T^3+a_4T^4+a_5T^5=0 \\
\dot{s}(T)=\dot{s}_T=\cdots=0 \\
\ddot{s}(T)=\ddot{s}_T=\cdots=0
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\
1 & T & T^2 & T^3 & T^4 & T^5 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 1 & 2T & 3T^2 & 4T^3 & 5T^4 \\
0 & 0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 6T & 12T^2 & 20T^3
\end{bmatrix}
\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \end{bmatrix} =
\begin{bmatrix} s_0 \\ s_T \\ \dot{s}_0 \\ \dot{s}_T \\ \ddot{s}_0 \\ \ddot{s}_T \end{bmatrix}
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\
1 & T & T^2 & T^3 & T^4 & T^5 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 1 & 2T & 3T^2 & 4T^3 & 5T^4 \\
0 & 0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 6T & 12T^2 & 20T^3
\end{bmatrix}
\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \end{bmatrix} =
\begin{bmatrix} s_0 \\ s_T \\ \dot{s}_0 \\ \dot{s}_T \\ \ddot{s}_0 \\ \ddot{s}_T \end{bmatrix}
\mathbf{A}
\mathbf{x}
\mathbf{b}
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\
1 & T & T^2 & T^3 & T^4 & T^5 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 1 & 2T & 3T^2 & 4T^3 & 5T^4 \\
0 & 0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 6T & 12T^2 & 20T^3
\end{bmatrix}
\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \end{bmatrix} =
\begin{bmatrix} s_0 \\ s_T \\ \dot{s}_0 \\ \dot{s}_T \\ \ddot{s}_0 \\ \ddot{s}_T \end{bmatrix}
\Rightarrow \mathbf{x}=\mathbf{A}^{-1}\mathbf{b}
Algunos detalles sobre el escalamiento
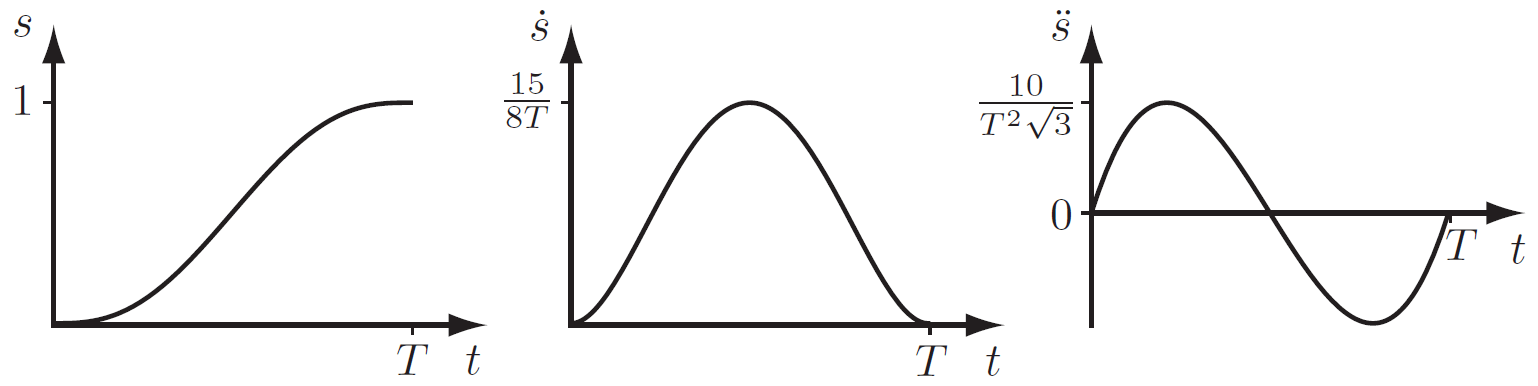
Algunos detalles sobre el escalamiento
\dot{\mathbf{q}}=\left(\mathbf{q}_f-\mathbf{q}_0\right)\dot{s}
dentro del recorrido formado mediante interpolación
\ddot{\mathbf{q}}=\left(\mathbf{q}_f-\mathbf{q}_0\right)\ddot{s}
Algunos detalles sobre el escalamiento
entonces, la velocidad máxima de la configuración se da en \(t=T/2\), mientras que las aceleraciones máximas ocurren en \(t=T/4\) y \(t=3T/4\)
Algunos detalles sobre el escalamiento
entonces, la velocidad máxima de la configuración se da en \(t=T/2\), mientras que las aceleraciones máximas ocurren en \(t=T/4\) y \(t=3T/4\)
estos máximos deben ser congruentes con lo que pueden brindar los actuadores
Algunos detalles sobre el escalamiento
entonces, la velocidad máxima de la configuración se da en \(t=T/2\), mientras que las aceleraciones máximas ocurren en \(t=T/4\) y \(t=3T/4\)
estos máximos deben ser congruentes con lo que pueden brindar los actuadores
en caso no, puede resolverse para \(T\) tal que los actuadores sean capaces de ejecutar la trayectoria
¿Limitantes?
la fuerte aceleración y desaceleración durante el método hace que no se esté aprovechando adecuadamente la potencia de los motores
¿Limitantes?
la fuerte aceleración y desaceleración durante el método hace que no se esté aprovechando adecuadamente la potencia de los motores
dicho de otra manera, la velocidad cambia mucho durante el recorrido
¿Limitantes?
la fuerte aceleración y desaceleración durante el método hace que no se esté aprovechando adecuadamente la potencia de los motores
dicho de otra manera, la velocidad cambia mucho durante el recorrido
una solución más eficiente...
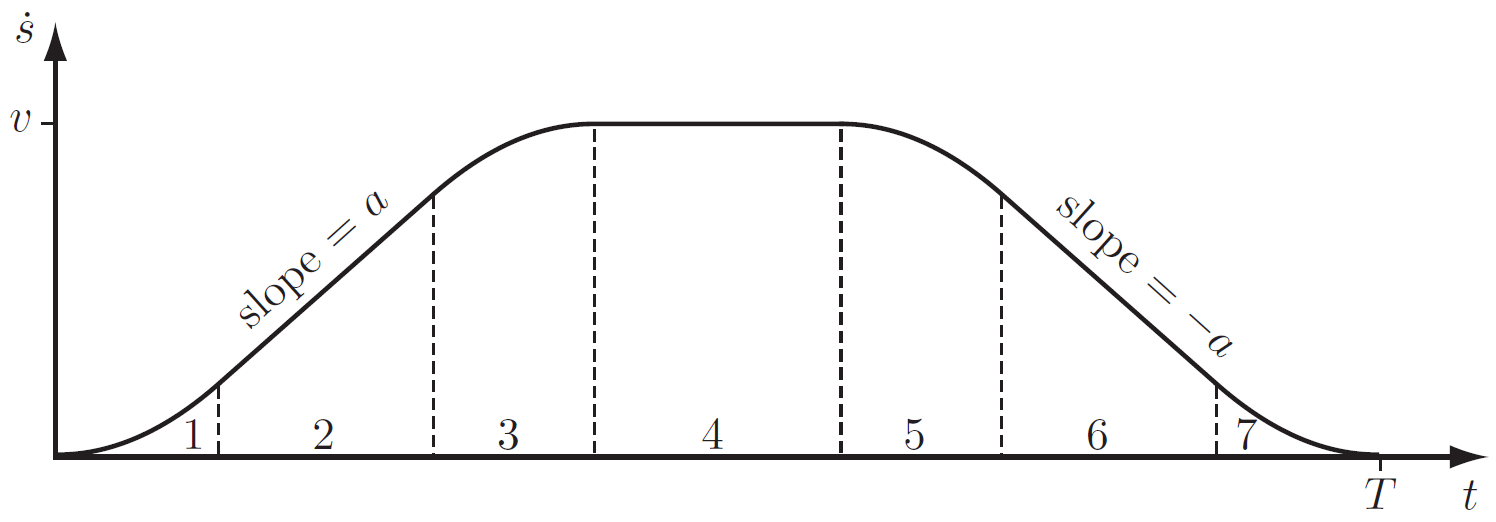
Perfiles de velocidad trapezoidal
t
t
t
T
\mathrm{pos}
\mathrm{vel}
\mathrm{acc}
Linear Segment with Parabolic Blends (LSPB)
a
v
\frac{v}{a}
T-\frac{v}{a}
Perfiles de velocidad trapezoidal
t
t
t
T
\mathrm{pos}
\mathrm{vel}
\mathrm{acc}
Linear Segment with Parabolic Blends (LSPB)
a
v
\frac{v}{a}
T-\frac{v}{a}
* siempre que \(v^2/a \le 1\), sino el perfil trapezoidal se convierte en un triángulo
Perfiles de velocidad trapezoidal
t
t
t
T
\mathrm{pos}
\mathrm{vel}
\mathrm{acc}
Linear Segment with Parabolic Blends (LSPB)
a
v
\frac{v}{a}
T-\frac{v}{a}
\ddot{s}(t)=a \\
\dot{s}(t)=at \\
s(t)=\frac{1}{2}at^2
para \(0\le t\le\frac{v}{a}\):
Perfiles de velocidad trapezoidal
t
t
t
T
\mathrm{pos}
\mathrm{vel}
\mathrm{acc}
Linear Segment with Parabolic Blends (LSPB)
a
v
\frac{v}{a}
T-\frac{v}{a}
\ddot{s}(t)=0 \\
\dot{s}(t)=v \\
s(t)=vt-\frac{v^2}{2a}
para \(\frac{v}{a} < t \le T-\frac{v}{a}\):
Perfiles de velocidad trapezoidal
t
t
t
T
\mathrm{pos}
\mathrm{vel}
\mathrm{acc}
Linear Segment with Parabolic Blends (LSPB)
a
v
\frac{v}{a}
T-\frac{v}{a}
\ddot{s}(t)=-a \\
\dot{s}(t)=a(T-t) \\
s(t)=\frac{2avT-2v^2-a^2(t-T)^2}{2a}
para \(T-\frac{v}{a} < t \le T\):
Detalles y limitantes
sólo pueden establecerse independientemente 2 de los 3 parámetros \(v, a\) y \(T\), por lo que hay tres opciones:
(todas las opciones garantizan que el perfil tenga tres segmentos y que pueda cumplirse con \(s(T)=1\))
Detalles y limitantes
sólo pueden establecerse independientemente 2 de los 3 parámetros \(v, a\) y \(T\), por lo que hay tres opciones:
1. Se escogen \(v\) y \(a\) tal que \(v^2/a\le 1\) y se resuelve para \(T\). Esto da el tiempo mínimo posible del movimiento si \(v\) y \(a\) corresponden a las velocidades y aceleraciones máximas posibles de la configuración.
T=\dfrac{a+v^2}{va}
Detalles y limitantes
sólo pueden establecerse independientemente 2 de los 3 parámetros \(v, a\) y \(T\), por lo que hay tres opciones:
2. Se escogen \(v\) y \(T\) tal que \(2 \ge vT > 1\) y se resuelve para \(a\).
a=\dfrac{v^2}{vT-1}
Detalles y limitantes
sólo pueden establecerse independientemente 2 de los 3 parámetros \(v, a\) y \(T\), por lo que hay tres opciones:
3. Se escogen \(a\) y \(T\) tal que \(aT^2 \ge 4\) y se resuelve para \(v\).
v=\dfrac{1}{2}\left(aT-\sqrt{a} \sqrt{aT^2-4}\right)
Detalles y limitantes
menos suave que el escalamiento polinomial, dado que la aceleración es discontinua (puede resolverse esto empleando una curva-S en su lugar)
Ejemplo
PUMA 560
\mathcal{C}: \ \mathbf{q} \in \mathbb{R}^6
\mathcal{T}: \ (x,y,z) \in \mathbb{R}^3
\(z\) cte.
>> mt3005_clase11_p2ptraj.mlx
\mathbf{T}_0
\mathbf{T}_f
Ejemplo
PUMA 560
\mathcal{C}: \ \mathbf{q} \in \mathbb{R}^6
\mathcal{T}: \ (x,y,z) \in \mathbb{R}^3
\(z\) cte.
>> mt3005_clase11_p2ptraj.mlx
\mathbf{T}_0
\mathbf{T}_f
¿Problema?
La interpolación lineal en \(\mathcal{C}\) NO produjo un movimiento lineal en \(\mathcal{T}\)
Ejemplo
PUMA 560
\mathcal{C}: \ \mathbf{q} \in \mathbb{R}^6
\mathcal{T}: \ (x,y,z) \in \mathbb{R}^3
\(z\) cte.
>> mt3005_clase11_p2ptraj.mlx
\mathbf{T}_0
\mathbf{T}_f
¿Problema?
La interpolación lineal en \(\mathcal{C}\) NO produjo un movimiento lineal en \(\mathcal{T}\)
esto no se esperaba del método, pero podría ser necesario
\mathbf{T}_0
\mathbf{T}_f
\mathbf{T}_0
\mathbf{T}_f
interpolación en \(\mathcal{T}\)
Interpolación en \(\mathcal{T}\)
en este caso ya no puede emplearse directamente la fórmula de interpolación, ¿Por qué?
{^B}\mathbf{T}_E(s) \to \boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix}
Interpolación en \(\mathcal{T}\)
en este caso ya no puede emplearse directamente la fórmula de interpolación, ¿Por qué?
{^B}\mathbf{T}_E(s) \to \boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix}
\mathbf{o}(s)=(1-s)\mathbf{o}_0+s\mathbf{o}_f
Interpolación en \(\mathcal{T}\)
en este caso ya no puede emplearse directamente la fórmula de interpolación, ¿Por qué?
{^B}\mathbf{T}_E(s) \to \boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix}
\mathbf{o}(s)=(1-s)\mathbf{o}_0+s\mathbf{o}_f
???
Interpolación en \(\mathcal{T}\)
{^B}\mathbf{T}_E(s) \to \boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix}
\mathcal{Q}(s)=\dfrac{\sin(1-s\theta)\mathcal{Q}_0+\sin(s\theta)\mathcal{Q}_f}{\sin(\theta)}
Spherical Linear Interpolation (SLERP)
\mathcal{Q}(s)
Interpolación en \(\mathcal{T}\)
{^B}\mathbf{T}_E(s) \to \boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix}
\mathcal{Q}(s)=\dfrac{\sin(1-s\theta)\mathcal{Q}_0+\sin(s\theta)\mathcal{Q}_f}{\sin(\theta)}
Spherical Linear Interpolation (SLERP)
\mathcal{Q}(s)
\theta=\eta_0\eta_f+\boldsymbol{\epsilon}_0^\top\boldsymbol{\epsilon}_f
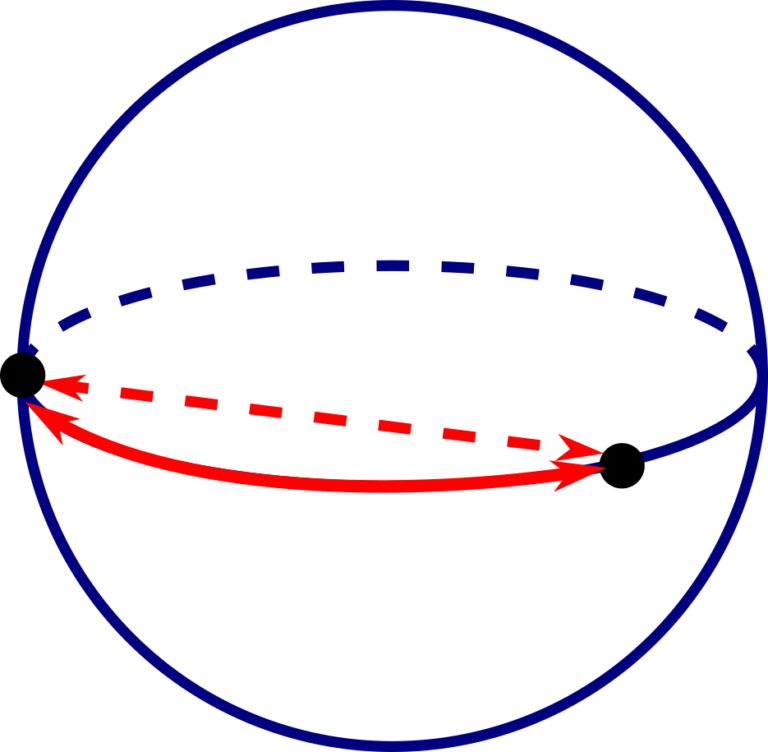
Interpolación en \(\mathcal{T}\)
y para finalizar debe regresarse la trayectoria al espacio de configuración
\boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix} \xrightarrow{\mathcal{K}^{-1}} \mathbf{q}(s) \to
servos
Interpolación en \(\mathcal{T}\)
y para finalizar debe regresarse la trayectoria al espacio de configuración
\boldsymbol{\xi}(s)=\begin{bmatrix} \mathbf{o}(s) \\ \boldsymbol{\theta}(s) \end{bmatrix} \xrightarrow{\mathcal{K}^{-1}} \mathbf{q}(s) \to
servos
>> mt3005_clase11_p2ptraj.mlx
¿Problemas?
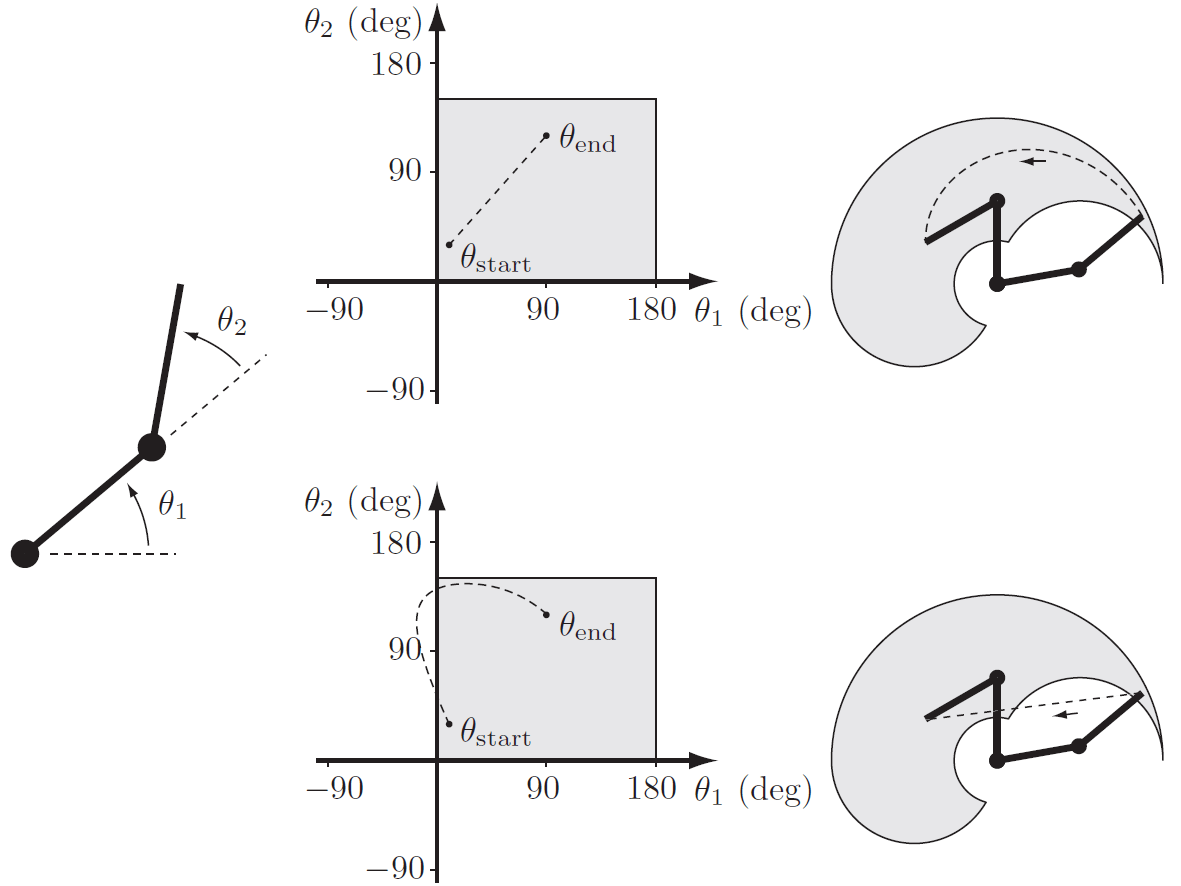
¿Problemas?
puede que los recorridos lineales en \(\mathcal{T}\) no caigan completamente dentro del espacio de trabajo del robot
Trayectorias multi-segmento
(a través de puntos vía)
se especifica una secuencia de poses específicas por las cuales debe pasar el efector final
se especifica una secuencia de poses específicas por las cuales debe pasar el efector final
qué tanto deberán respetarse las poses específicas dependerá de la aplicación
se especifica una secuencia de poses específicas por las cuales debe pasar el efector final
Ejemplo: soldadura, pintura, etc.
qué tanto deberán respetarse las poses específicas dependerá de la aplicación
¿Opciones?
1. Emplear una secuencia consecutiva de trayectorias punto a punto.
¿Opciones?
1. Emplear una secuencia consecutiva de trayectorias punto a punto.
es probable que deban cambiarse las condiciones de frontera en los escalamientos de tiempo para que el robot no se encuentre acelerando y desacelerando constantemente
¿Opciones?
1. Emplear una secuencia consecutiva de trayectorias punto a punto.
pero se cae al problema de seleccionar correctamente las velocidades y aceleraciones en los puntos y resolver en simultáneo para todos los escalamientos de tiempo (sección 9.3 de [Lynch&Park])
¿Opciones?
1. Emplear una secuencia consecutiva de trayectorias punto a punto.
pero se cae al problema de seleccionar correctamente las velocidades y aceleraciones en los puntos y resolver en simultáneo para todos los escalamientos de tiempo (sección 9.3 de [Lynch&Park])
una mejor opción...
¿Opciones?
2. Encontrar la trayectoria directamente mediante polinomios de 5to orden o LSPBs.
¿Opciones?
2. Encontrar la trayectoria directamente mediante polinomios de 5to orden o LSPBs.
en lugar de calcular el recorrido y el escalamiento de tiempo por aparte, se plantea el problema de interpolación polinomial | LSPB directamente en el tiempo
¿Opciones?
2. Encontrar la trayectoria directamente mediante polinomios de 5to orden o LSPBs.
en MATLAB, tanto la Robotics Toolbox como la Robotics Systems Toolbox tienen rutinas especializadas para hacer esto
>> mt3005_clase11_viatraj.m
¿Opciones?
2. Encontrar la trayectoria directamente mediante polinomios de 5to orden o LSPBs.
sin embargo, igualmente debe considerarse la forma en que se definen las velocidades y aceleraciones en los puntos vía
¿Opciones?
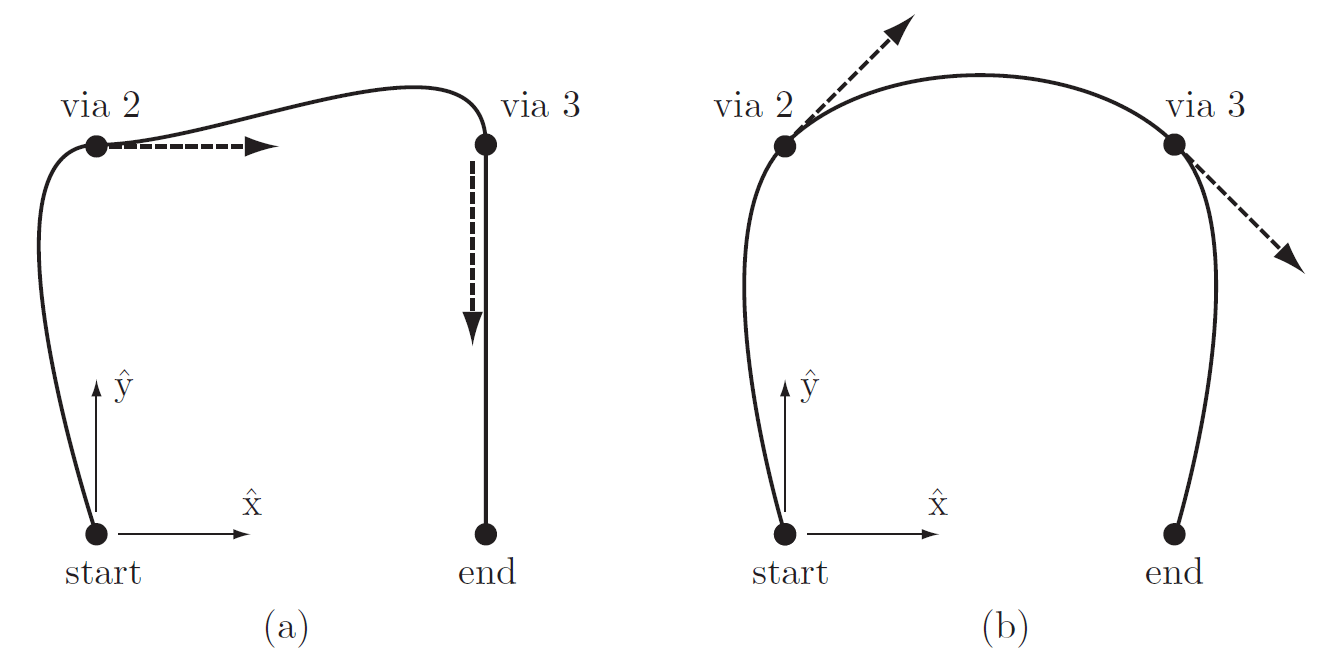
¿Opciones?
3. Utilizar interpolación mediante splines
directamente en el tiempo.
¿Opciones?
3. Utilizar interpolación mediante splines
directamente en el tiempo.
las splines presentan un comportamiento similar al de la interpolación mediante polinomios pero evitan el fenómeno de Runge, aunque no garantizan pasar exactamente sobre los puntos vía
¿Opciones?
3. Utilizar interpolación mediante splines
directamente en el tiempo.
igualmente existen rutinas especializadas como las de la Robotics System Toolbox de MATLAB
>> mt3005_clase11_viatraj.m
MT3005 - Lecture 11 (2025)
By Miguel Enrique Zea Arenales
