Estabilización de sistemas no lineales mediante linealización

IE3041 - Sistemas de Control 2

Regresando a sistemas no lineales

similar al caso de estabilidad, tratemos de aplicar las herramientas de estabilización desarrolladas para sistemas LTI pero en el caso de sistemas no lineales



linealización

linealización
LQR
se encuentra en las coordenadas linealizadas, por lo que es necesario regresarlo a las coordenadas del sistema no lineal original
se encuentra en las coordenadas linealizadas, por lo que es necesario regresarlo a las coordenadas del sistema no lineal original
se encuentra en las coordenadas linealizadas, por lo que es necesario regresarlo a las coordenadas del sistema no lineal original
control LTI que estabiliza el punto \(\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\) del sistema no lineal*
feedback
feedforward
control LTI que estabiliza el punto \(\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\) del sistema no lineal*
feedback
feedforward
el LQR ya NO es óptimo para el caso no lineal
control LTI que estabiliza el punto \(\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\) del sistema no lineal*
feedback
feedforward
el LQR ya NO es óptimo para el caso no lineal
control LTI que estabiliza el punto \(\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\) del sistema no lineal*
*siempre y cuando \(\mathbf{x}_0 \in\) región de atracción del punto de equilibrio u operación del sistema en lazo cerrado
Arquitectura del controlador
observador de estado
Arquitectura del controlador
observador de estado
Arquitectura del controlador
observador de estado
Arquitectura del controlador
observador de estado
Arquitectura del controlador
observador de estado
feedforward para velocidad y feedback para robustez
Arquitectura del controlador
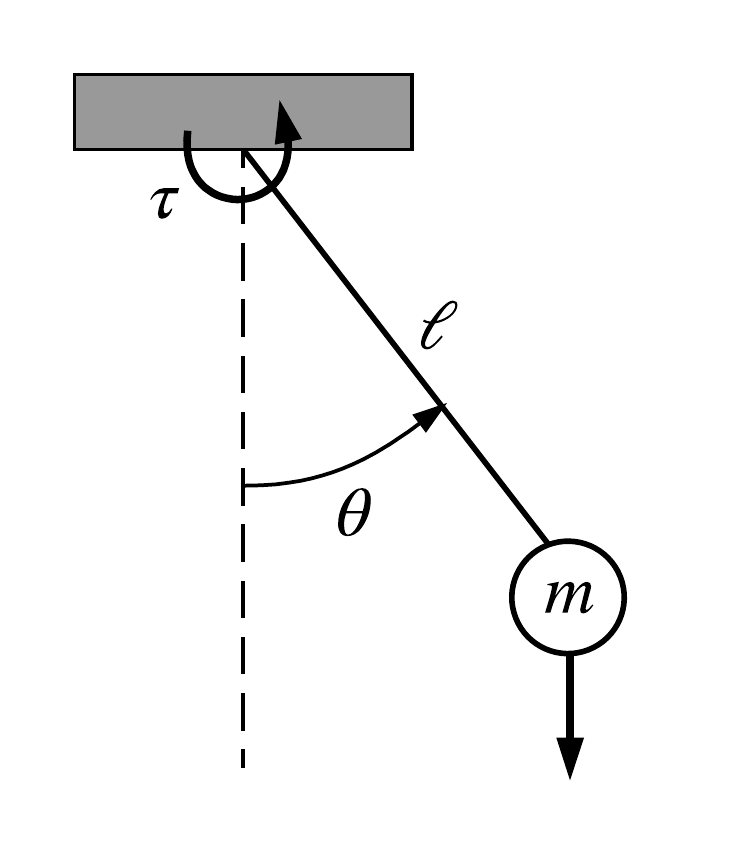
Ejemplo: estabilización péndulo simple

Ejemplo: estabilización péndulo simple

Ejemplo: estabilización péndulo simple
Procedimiento general: >> ie3041_clase7_procedimiento.mlx
Ejemplo péndulo: >> ie3041_clase7_pendstab.m
Control de alta ganancia
es posible ampliar (hasta el punto que lo permitan los actuadores) la región de atracción del punto de equilibrio u operación a estabilizar, incrementando la ganancia del controlador
>> ie3041_clase7_stabilize2d.m
Caso especial para sistemas mecánicos
para el caso especial de sistemas mecánicos completamente actuados y con \(\mathbf{B}\left(\mathbf{q}\right)\) invertible, se tiene que:
estabiliza el punto \(\left(\mathbf{q}_{ss},\mathbf{0}\right)\) del sistema mecánico
Control PD para sistemas mecánicos
para el caso especial de sistemas mecánicos completamente actuados y con \(\mathbf{B}\left(\mathbf{q}\right)\) invertible, se tiene que:
estabiliza el punto \(\left(\mathbf{q}_{ss},\mathbf{0}\right)\) del sistema mecánico
Control PD para sistemas mecánicos
para el caso especial de sistemas mecánicos completamente actuados y con \(\mathbf{B}\left(\mathbf{q}\right)\) invertible, se tiene que:
estabiliza el punto \(\left(\mathbf{q}_{ss},\mathbf{0}\right)\) del sistema mecánico
Control PD para sistemas mecánicos
IE3041 - Lecture 7 (2025)
By Miguel Enrique Zea Arenales
IE3041 - Lecture 7 (2025)
- 322



