Control integral y gain scheduling
IE3041 - Sistemas de Control 2
Mejorando el controlador lineal
luego de aplicar el controlador lineal
\mathbf{u}=-\mathbf{K}\left(\mathbf{x}-\mathbf{x}_{ss}\right)+\mathbf{u}_{ss}
luego de aplicar el controlador lineal
\mathbf{u}=-\mathbf{K}\left(\mathbf{x}-\mathbf{x}_{ss}\right)+\mathbf{u}_{ss}
a distintos casos no lineales, observamos que
\text{buen rendimiento}\left(\text{región de atracción de } (\mathbf{x}_{ss}, \mathbf{u}_{ss})\right)
luego de aplicar el controlador lineal
\mathbf{u}=-\mathbf{K}\left(\mathbf{x}-\mathbf{x}_{ss}\right)+\mathbf{u}_{ss}
a distintos casos no lineales, observamos que
\text{buen rendimiento}\left(\text{región de atracción de } (\mathbf{x}_{ss}, \mathbf{u}_{ss})\right)
por ejemplo:
drones \(\to\) buen rendimiento
péndulos* \(\to\) meh rendimiento
luego de aplicar el controlador lineal
\mathbf{u}=-\mathbf{K}\left(\mathbf{x}-\mathbf{x}_{ss}\right)+\mathbf{u}_{ss}
a distintos casos no lineales, observamos que
\text{buen rendimiento}\left(\text{región de atracción de } (\mathbf{x}_{ss}, \mathbf{u}_{ss})\right)
sin mencionar que pasamos de una única referencia \(r\) en el caso clásico a múltiples en la forma de \(\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)\)
considerando estas limitantes, ¿Podremos mejorar el controlador antes de acudir a métodos de control más complejos?
considerando estas limitantes, ¿Podremos mejorar el controlador antes de acudir a métodos de control más complejos?
SÍ, pero sólo hasta cierto punto
considerando estas limitantes, ¿Podremos mejorar el controlador antes de acudir a métodos de control más complejos?
SÍ, pero sólo hasta cierto punto
específicamente, estudiaremos dos "mejoras" en particular:
\(\to\) control integral para rastreo
\(\to\) gain scheduling
Control integral para rastreo
Motivación e intuición previa
estabilizar con LQR
m
b
k
f
p
Motivación e intuición previa
m\ddot{p}+b\dot{p}+kp=f
x_1=p \\
x_2=\dot{p}
u=f \\
y=p
estabilizar con LQR
m
b
k
f
p
Motivación e intuición previa
m\ddot{p}+b\dot{p}+kp=f
\begin{aligned} \dot{\mathbf{x}}=\begin{bmatrix} 0 & 1 \\ -k/m & -b/m \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0 \\ 1/m \end{bmatrix}u \\
y=\begin{bmatrix} 1 & 0 \end{bmatrix}\mathbf{x} \end{aligned}
x_1=p \\
x_2=\dot{p}
u=f \\
y=p
estabilizar con LQR
m
b
k
f
p
Motivación e intuición previa
estabilizar con LQR
m
b
k
f
p
u^\star=-\mathbf{K}\mathbf{x}\\
u^\star=-\begin{bmatrix} k_1 & k_2\end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\
u^\star=-k_1x_1-k_2x_2
Motivación e intuición previa
estabilizar con LQR
m
b
k
f
p
u^\star=-\mathbf{K}\mathbf{x}\\
u^\star=-\begin{bmatrix} k_1 & k_2\end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\
u^\star=-k_1x_1-k_2x_2
x_1=p, \ x_2=\dot{p}, \ y=x_1=p
\Rightarrow u=-k_1y-k_2\dot{y}
Motivación e intuición previa
estabilizar con LQR
m
b
k
f
p
u^\star=-\mathbf{K}\mathbf{x}\\
u^\star=-\begin{bmatrix} k_1 & k_2\end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\
u^\star=-k_1x_1-k_2x_2
x_1=p, \ x_2=\dot{p}, \ y=x_1=p
\Rightarrow u=-k_1y-k_2\dot{y}=-k_Py-k_D\dot{y}
(output feedback)
proporcional
derivativo
control PD
Motivación e intuición previa
por lo tanto
LQR \(\sim\) control PD
Motivación e intuición previa
por lo tanto
LQR \(\sim\) control PD
bajo la perspectiva clásica entonces, ¿Qué le falta al LQR?
una parte integral
\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)
\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)
\left(\mathbf{x}^*,\mathbf{u}^*\right) \text{ o }\\
\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)
\left(\mathbf{x}^*,\mathbf{u}^*\right) \text{ o }\\
\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
\to \mathbf{r}=\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)
\left(\mathbf{x}^*,\mathbf{u}^*\right) \text{ o }\\
\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
\to \mathbf{r}=\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
referencia
\(\mathbf{y}_r=\mathbf{h}_r\left(\mathbf{x},\mathbf{u}\right)\equiv\) salida virtual de control
\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{y}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)
\left(\mathbf{x}^*,\mathbf{u}^*\right) \text{ o }\\
\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
\to \mathbf{r}=\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
referencia
NO es una salida real
\(\mathbf{y}_r=\mathbf{h}_r\left(\mathbf{x},\mathbf{u}\right)\equiv\) salida virtual de control
debe ser subconjunto de
rastreo \(\equiv\) estabilizar el error integral \(\boldsymbol{\sigma}(t)\)
rastreo \(\equiv\) estabilizar el error integral \(\boldsymbol{\sigma}(t)\)
\boldsymbol{\sigma}(t)=\displaystyle\int_{t_0}^{t} \left[\mathbf{r}(\tau)-\mathbf{y}_r(\tau)\right]d\tau \\
\boldsymbol{\sigma}(t)=\displaystyle\int_{t_0}^{t} \left[\mathbf{r}(\tau)-\mathbf{h}_r\left(\mathbf{x}(\tau),\mathbf{u}(\tau)\right)\right]d\tau
rastreo \(\equiv\) estabilizar el error integral \(\boldsymbol{\sigma}(t)\)
\boldsymbol{\sigma}(t)=\displaystyle\int_{t_0}^{t} \left[\mathbf{r}(\tau)-\mathbf{y}_r(\tau)\right]d\tau \\
\boldsymbol{\sigma}(t)=\displaystyle\int_{t_0}^{t} \left[\mathbf{r}(\tau)-\mathbf{h}_r\left(\mathbf{x}(\tau),\mathbf{u}(\tau)\right)\right]d\tau
¿Por qué?
\dot{\boldsymbol{\sigma}}=\mathbf{f}_{\sigma}\left(\boldsymbol{\sigma},\mathbf{x},\mathbf{u}\right)=\mathbf{r}-\mathbf{h}_r\left(\mathbf{x}, \mathbf{u}\right)
rastreo \(\equiv\) estabilizar el error integral \(\boldsymbol{\sigma}(t)\)
\boldsymbol{\sigma}(t)=\displaystyle\int_{t_0}^{t} \left[\mathbf{r}(\tau)-\mathbf{y}_r(\tau)\right]d\tau \\
\boldsymbol{\sigma}(t)=\displaystyle\int_{t_0}^{t} \left[\mathbf{r}(\tau)-\mathbf{h}_r\left(\mathbf{x}(\tau),\mathbf{u}(\tau)\right)\right]d\tau
¿Por qué?
\dot{\boldsymbol{\sigma}}=\mathbf{f}_{\sigma}\left(\boldsymbol{\sigma},\mathbf{x},\mathbf{u}\right)=\mathbf{r}-\mathbf{h}_r\left(\mathbf{x}, \mathbf{u}\right)
desventaja: requiere \(\mathbf{r}\) constante
problema combinado de rastreo + estabilización
\dot{\boldsymbol{\xi}}=\mathbf{F}\left(\boldsymbol{\xi},\mathbf{u}\right)=
\begin{bmatrix} \mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{f}_{\sigma}\left(\boldsymbol{\sigma},\mathbf{x},\mathbf{u}\right)\end{bmatrix}=
\begin{bmatrix} \mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{r}-\mathbf{h}_r\left(\mathbf{x},\mathbf{u}\right)\end{bmatrix}
problema combinado de rastreo + estabilización
\dot{\boldsymbol{\xi}}=\mathbf{F}\left(\boldsymbol{\xi},\mathbf{u}\right)=
\begin{bmatrix} \mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{f}_{\sigma}\left(\boldsymbol{\sigma},\mathbf{x},\mathbf{u}\right)\end{bmatrix}=
\begin{bmatrix} \mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{r}-\mathbf{h}_r\left(\mathbf{x},\mathbf{u}\right)\end{bmatrix}
\boldsymbol{\xi}=\begin{bmatrix} \mathbf{x} \\ \boldsymbol{\sigma}\end{bmatrix}
nuevo estado
problema combinado de rastreo + estabilización
\dot{\boldsymbol{\xi}}=\mathbf{F}\left(\boldsymbol{\xi},\mathbf{u}\right)=
\begin{bmatrix} \mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{f}_{\sigma}\left(\boldsymbol{\sigma},\mathbf{x},\mathbf{u}\right)\end{bmatrix}=
\begin{bmatrix} \mathbf{f}\left(\mathbf{x},\mathbf{u}\right) \\
\mathbf{r}-\mathbf{h}_r\left(\mathbf{x},\mathbf{u}\right)\end{bmatrix}
\boldsymbol{\xi}=\begin{bmatrix} \mathbf{x} \\ \boldsymbol{\sigma}\end{bmatrix}
\left(\boldsymbol{\xi}_{ss},\mathbf{u}_{ss}\right) \equiv \left(\mathbf{x}_{ss}, \boldsymbol{\sigma}_{ss},\mathbf{u}_{ss}\right)
nuevo estado
nuevo punto de operación
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
para sintetizar el controlador primero se genera el sistema LTI aumentado
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\mathbf{z}=\boldsymbol{\xi}-\boldsymbol{\xi}_{ss} \\
\mathbf{v}=\mathbf{u}-\mathbf{u}_{ss} \\
\mathbf{w}=\mathbf{y}_r-\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
para sintetizar el controlador primero se genera el sistema LTI aumentado
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\mathbf{z}=\boldsymbol{\xi}-\boldsymbol{\xi}_{ss} \\
\mathbf{v}=\mathbf{u}-\mathbf{u}_{ss} \\
\mathbf{w}=\mathbf{y}_r-\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)
\mathbf{r}
para sintetizar el controlador primero se genera el sistema LTI aumentado
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{A}}=\begin{bmatrix} \mathbf{A} & \mathbf{0}_{n \times p} \\ -\mathbf{C}_r & \mathbf{0}_{p \times p} \end{bmatrix}
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{A}}=\begin{bmatrix} \mathbf{A} & \mathbf{0}_{n \times p} \\ -\mathbf{C}_r & \mathbf{0}_{p \times p} \end{bmatrix}
\mathbf{A}=\dfrac{\partial \mathbf{f}\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{x}}
-\mathbf{C}_r=\dfrac{\partial \mathbf{f}_\sigma\left(\boldsymbol{\sigma}_{ss},\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{x}}=-\dfrac{\partial \mathbf{h}_r\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{x}}
misma matriz de la linealización "normal"
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{B}}=\begin{bmatrix} \mathbf{B} \\ -\mathbf{D}_r \end{bmatrix}
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{B}}=\begin{bmatrix} \mathbf{B} \\ -\mathbf{D}_r \end{bmatrix}
\mathbf{B}=\dfrac{\partial \mathbf{f}\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}
-\mathbf{D}_r=\dfrac{\partial \mathbf{f}_\sigma\left(\boldsymbol{\sigma}_{ss},\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}=-\dfrac{\partial \mathbf{h}_r\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}
misma matriz de la linealización "normal"
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{B}}=\begin{bmatrix} \mathbf{B} \\ -\mathbf{D}_r \end{bmatrix} \to \begin{bmatrix} \mathbf{B} \\ \mathbf{0}_{p \times m} \end{bmatrix}
\mathbf{B}=\dfrac{\partial \mathbf{f}\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}
-\mathbf{D}_r=\dfrac{\partial \mathbf{f}_\sigma\left(\boldsymbol{\sigma}_{ss},\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}=-\dfrac{\partial \mathbf{h}_r\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}
misma matriz de la linealización "normal"
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{C}}=\begin{bmatrix} \mathbf{C}_r & \mathbf{0}_{p \times p} \end{bmatrix}
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{C}}=\begin{bmatrix} \mathbf{C}_r & \mathbf{0}_{p \times p} \end{bmatrix}
\mathbf{C}_r=\dfrac{\partial \mathbf{h}_r\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{x}}
misma matriz de la linealización "normal" pero usando la salida virtual
\begin{cases} \dot{\mathbf{z}} = \boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\mathbf{w} = \boldsymbol{\mathcal{C}}\mathbf{z}+\boldsymbol{\mathcal{D}}\mathbf{v} \\
\mathbf{z}(t_0)=\mathbf{z}_0=\begin{bmatrix} \delta\mathbf{x}_{ss} \\ \delta\boldsymbol{\sigma}_{ss} \end{bmatrix}
\end{cases}
\boldsymbol{\mathcal{D}}=\mathbf{D}_r=\dfrac{\partial \mathbf{h}_r\left(\mathbf{x}_{ss}, \mathbf{u}_{ss}\right)}{\partial \mathbf{u}}
misma matriz de la linealización "normal" pero usando la salida virtual
Control Lineal Cuadrático Integral (LQI)
\begin{aligned}
\mathbf{v}^\star(t) = & \displaystyle\arg\min_{\mathbf{v(t)}} \displaystyle\int_{t_0}^{\infty} \left[\mathbf{z}(t)^\top \boldsymbol{\mathcal{Q}}\mathbf{z}(t)+\mathbf{v}(t)^\top \boldsymbol{\mathcal{R}}\mathbf{v}(t)\right]dt \\
& \textrm{s.t.} \quad \dot{\mathbf{z}}=\boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\end{aligned}
Control Lineal Cuadrático Integral (LQI)
\begin{aligned}
\mathbf{v}^\star(t) = & \displaystyle\arg\min_{\mathbf{v(t)}} \displaystyle\int_{t_0}^{\infty} \left[\mathbf{z}(t)^\top \boldsymbol{\mathcal{Q}}\mathbf{z}(t)+\mathbf{v}(t)^\top \boldsymbol{\mathcal{R}}\mathbf{v}(t)\right]dt \\
& \textrm{s.t.} \quad \dot{\mathbf{z}}=\boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\end{aligned}
matrices de penalización para el sistema aumentado
Control Lineal Cuadrático Integral (LQI)
\begin{aligned}
\mathbf{v}^\star(t) = & \displaystyle\arg\min_{\mathbf{v(t)}} \displaystyle\int_{t_0}^{\infty} \left[\mathbf{z}(t)^\top \boldsymbol{\mathcal{Q}}\mathbf{z}(t)+\mathbf{v}(t)^\top \boldsymbol{\mathcal{R}}\mathbf{v}(t)\right]dt \\
& \textrm{s.t.} \quad \dot{\mathbf{z}}=\boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\end{aligned}
\mathbf{v}^\star=-\boldsymbol{\mathcal{K}}\mathbf{z}
matrices de penalización para el sistema aumentado
Control Lineal Cuadrático Integral (LQI)
\begin{aligned}
\mathbf{v}^\star(t) = & \displaystyle\arg\min_{\mathbf{v(t)}} \displaystyle\int_{t_0}^{\infty} \left[\mathbf{z}(t)^\top \boldsymbol{\mathcal{Q}}\mathbf{z}(t)+\mathbf{v}(t)^\top \boldsymbol{\mathcal{R}}\mathbf{v}(t)\right]dt \\
& \textrm{s.t.} \quad \dot{\mathbf{z}}=\boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{v} \\
\end{aligned}
\mathbf{v}^\star=-\boldsymbol{\mathcal{K}}\mathbf{z}
\Rightarrow \mathbf{u}-\mathbf{u}_{ss}=-\boldsymbol{\mathcal{K}}\left(\boldsymbol{\xi}-\boldsymbol{\xi}_{ss}\right)=
-\begin{bmatrix} \mathbf{K}_1 & \mathbf{K}_2 \end{bmatrix}\left(\begin{bmatrix} \mathbf{x}-\mathbf{x}_{ss} \\ \boldsymbol{\sigma}-\boldsymbol{\sigma}_{ss} \end{bmatrix}\right)
matrices de penalización para el sistema aumentado
Control Lineal Cuadrático Integral (LQI)
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}+\mathbf{K}_1\mathbf{x}_{ss}+\mathbf{K}_2\boldsymbol{\sigma}_{ss}+\mathbf{u}_{ss}
Control Lineal Cuadrático Integral (LQI)
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}+\mathbf{K}_1\mathbf{x}_{ss}+\mathbf{K}_2\boldsymbol{\sigma}_{ss}+\mathbf{u}_{ss}
state feedback
offset (feedforward)
Control Lineal Cuadrático Integral (LQI)
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}+\mathbf{K}_1\mathbf{x}_{ss}+\mathbf{K}_2\boldsymbol{\sigma}_{ss}+\mathbf{u}_{ss}
state feedback
offset (feedforward)
puede emplearse \(\boldsymbol{\sigma}_{ss}\) a conveniencia, cancelando el offset y obteniendo
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}=-\boldsymbol{\mathcal{K}}\boldsymbol{\xi}
Control Lineal Cuadrático Integral (LQI)
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}+\mathbf{K}_1\mathbf{x}_{ss}+\mathbf{K}_2\boldsymbol{\sigma}_{ss}+\mathbf{u}_{ss}
state feedback
offset (feedforward)
puede emplearse \(\boldsymbol{\sigma}_{ss}\) a conveniencia, cancelando el offset y obteniendo
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}=-\boldsymbol{\mathcal{K}}\boldsymbol{\xi}
control PD
control I
\(\approx\) control PID
Control Lineal Cuadrático Integral (LQI)
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}+\mathbf{K}_1\mathbf{x}_{ss}+\mathbf{K}_2\boldsymbol{\sigma}_{ss}+\mathbf{u}_{ss}
state feedback
offset (feedforward)
puede emplearse \(\boldsymbol{\sigma}_{ss}\) a conveniencia, cancelando el offset y obteniendo
\mathbf{u}=-\mathbf{K}_1\mathbf{x}-\mathbf{K}_2\boldsymbol{\sigma}=-\boldsymbol{\mathcal{K}}\boldsymbol{\xi}
control PD
control I
\(\approx\) control PID
en esencia consiste en el mismo controlador lineal pero empleando la parte integral para "calcular" \((\mathbf{x}_{ss}, \mathbf{u}_{ss})\) pero en lazo cerrado
\mathbf{f}
\boldsymbol{\int}
\mathbf{u}
\mathbf{y}
\dot{\mathbf{x}}
\mathbf{x}
\mathbf{h}
\mathbf{f}
\boldsymbol{\int}
\mathbf{u}
\mathbf{y}
\dot{\mathbf{x}}
\mathbf{x}
\mathbf{h}
\mathbf{h}_r
\mathbf{y}_r
\mathbf{f}
\boldsymbol{\int}
\mathbf{u}
\mathbf{y}
\dot{\mathbf{x}}
\mathbf{x}
\mathbf{K}_1
\mathbf{x}
\mathbf{h}
\boldsymbol{-}
\mathbf{h}_r
\mathbf{y}_r
observador
\mathbf{f}
\boldsymbol{\int}
\mathbf{u}
\mathbf{y}
\dot{\mathbf{x}}
\mathbf{x}
\mathbf{K}_1
\mathbf{x}
\mathbf{h}
\boldsymbol{-}
\boldsymbol{+}
\boldsymbol{-}
\mathbf{r}
\mathbf{h}_r
\mathbf{y}_r
\mathbf{r}-\mathbf{y}_r
observador
\mathbf{f}
\boldsymbol{\int}
\mathbf{u}
\mathbf{y}
\dot{\mathbf{x}}
\mathbf{x}
\mathbf{K}_1
\mathbf{x}
\mathbf{h}
\boldsymbol{-}
\boldsymbol{+}
\boldsymbol{-}
\mathbf{r}
\mathbf{h}_r
\boldsymbol{\int}
\mathbf{K}_2
\boldsymbol{-}
\mathbf{y}_r
\mathbf{r}-\mathbf{y}_r
\boldsymbol{\sigma}
control LQI | servo LQ
observador
\mathbf{f}
\boldsymbol{\int}
\mathbf{u}
\mathbf{y}
\dot{\mathbf{x}}
\mathbf{x}
\mathbf{K}_1
\mathbf{x}
\mathbf{h}
\boldsymbol{-}
\boldsymbol{+}
\boldsymbol{-}
\mathbf{r}
\mathbf{h}_r
\boldsymbol{\int}
\mathbf{K}_2
\boldsymbol{-}
\mathbf{y}_r
\mathbf{r}-\mathbf{y}_r
\boldsymbol{\sigma}
control LQI | servo LQ
>> ie3041_clase10_dpend.m
observador
Sobre el LQI para sistemas no lineales
si bien la dinámica de \(\boldsymbol{\sigma}\) requirió \(\mathbf{r}=\mathrm{cte.}\) para no depender de ella, no implica (necesariamente) que esta no pueda variar en el tiempo
Sobre el LQI para sistemas no lineales
si bien la dinámica de \(\boldsymbol{\sigma}\) requirió \(\mathbf{r}=\mathrm{cte.}\) para no depender de ella, no implica (necesariamente) que esta no pueda variar en el tiempo
sin embargo, \(\boldsymbol{\mathcal{A}}, \boldsymbol{\mathcal{B}}, \boldsymbol{\mathcal{C}}, \boldsymbol{\mathcal{D}}\) se calcularon para un \(\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\) fijo por lo que cambios en la referencia implican recalcular el punto de operación y la linealización
Sobre el LQI para sistemas no lineales
para solventar esto puede plantearse el siguiente sistema no lineal de ecuaciones
\mathbf{F}(\mathbf{z})=\mathbf{F}\left(\mathbf{x}_{ss},\mathbf{u}_{ss},\mathbf{r}\right)=\begin{bmatrix} \mathbf{f}\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right) \\
\mathbf{r}-\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\end{bmatrix}=\mathbf{0}
Sobre el LQI para sistemas no lineales
para solventar esto puede plantearse el siguiente sistema no lineal de ecuaciones
\mathbf{F}(\mathbf{z})=\mathbf{F}\left(\mathbf{x}_{ss},\mathbf{u}_{ss},\mathbf{r}\right)=\begin{bmatrix} \mathbf{f}\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right) \\
\mathbf{r}-\mathbf{h}_r\left(\mathbf{x}_{ss},\mathbf{u}_{ss}\right)\end{bmatrix}=\mathbf{0}
y resolver por Newton, inicializando con la solución al sistema previo para agilizar la convergencia y que esta tenga la tendencia a mantenerse congruente
El LQI para sistemas LTI
para el caso LTI la situación se simplifica considerablemente
\begin{aligned}
& \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\
& \mathbf{y}_r=\mathbf{C}_r\mathbf{x}+\mathbf{D}_r\mathbf{u} \\
& \dot{\boldsymbol{\sigma}}=\mathbf{r}-\mathbf{y}_r=\mathbf{r}-\mathbf{C}_r\mathbf{x}-\mathbf{D}_r\mathbf{u} \\
& \mathbf{Q}=\mathbf{I}_{n}, \quad \mathbf{R}=\mathbf{I}_{m}
\end{aligned}
El LQI para sistemas LTI
para el caso LTI la situación se simplifica considerablemente
\begin{aligned}
& \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\
& \mathbf{y}_r=\mathbf{C}_r\mathbf{x}+\mathbf{D}_r\mathbf{u} \\
& \dot{\boldsymbol{\sigma}}=\mathbf{r}-\mathbf{y}_r=\mathbf{r}-\mathbf{C}_r\mathbf{x}-\mathbf{D}_r\mathbf{u} \\
& \mathbf{Q}=\mathbf{I}_{n}, \quad \mathbf{R}=\mathbf{I}_{m}
\end{aligned}
\begin{aligned}
\dot{\mathbf{z}}=\boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{u}+\begin{bmatrix} \mathbf{0}_{n \times p} \\ \mathbf{I}_{p} \end{bmatrix}\mathbf{r} \\
\boldsymbol{\mathcal{A}}=\begin{bmatrix} \mathbf{A} & \mathbf{0}_{n \times p} \\ -\mathbf{C}_r & \mathbf{0}_{p \times p} \end{bmatrix}, \ \ \boldsymbol{\mathcal{B}}=\begin{bmatrix} \mathbf{B} \\ -\mathbf{D}_r \end{bmatrix} \\
\boldsymbol{\mathcal{Q}}=\mathbf{I}_{n+p}, \quad \boldsymbol{\mathcal{R}}=\mathbf{I}_{m}
\end{aligned}
El LQI para sistemas LTI
para el caso LTI la situación se simplifica considerablemente
\begin{aligned}
& \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\
& \mathbf{y}_r=\mathbf{C}_r\mathbf{x}+\mathbf{D}_r\mathbf{u} \\
& \dot{\boldsymbol{\sigma}}=\mathbf{r}-\mathbf{y}_r=\mathbf{r}-\mathbf{C}_r\mathbf{x}-\mathbf{D}_r\mathbf{u} \\
& \mathbf{Q}=\mathbf{I}_{n}, \quad \mathbf{R}=\mathbf{I}_{m}
\end{aligned}
\begin{aligned}
\dot{\mathbf{z}}=\boldsymbol{\mathcal{A}}\mathbf{z}+\boldsymbol{\mathcal{B}}\mathbf{u}+\begin{bmatrix} \mathbf{0}_{n \times p} \\ \mathbf{I}_{p} \end{bmatrix}\mathbf{r} \\
\boldsymbol{\mathcal{A}}=\begin{bmatrix} \mathbf{A} & \mathbf{0}_{n \times p} \\ -\mathbf{C}_r & \mathbf{0}_{p \times p} \end{bmatrix}, \ \ \boldsymbol{\mathcal{B}}=\begin{bmatrix} \mathbf{B} \\ -\mathbf{D}_r \end{bmatrix} \\
\boldsymbol{\mathcal{Q}}=\mathbf{I}_{n+p}, \quad \boldsymbol{\mathcal{R}}=\mathbf{I}_{m}
\end{aligned}
\mathbf{z}=\begin{bmatrix} \mathbf{x} \\ \boldsymbol{\sigma} \end{bmatrix} \\
\mathbf{M}
El LQI para sistemas LTI
para el caso LTI la situación se simplifica considerablemente
>> \boldsymbol{\mathcal{K}}=\mathrm{lqr}\left(\boldsymbol{\mathcal{A}},\boldsymbol{\mathcal{B}},\boldsymbol{\mathcal{Q}},\boldsymbol{\mathcal{R}}\right) \\
=\mathrm{lqi}\left(\mathrm{ss}\left(\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}\right), \mathbf{Q}, \mathbf{R}\right)
El LQI para sistemas LTI
para el caso LTI la situación se simplifica considerablemente
>> \boldsymbol{\mathcal{K}}=\mathrm{lqr}\left(\boldsymbol{\mathcal{A}},\boldsymbol{\mathcal{B}},\boldsymbol{\mathcal{Q}},\boldsymbol{\mathcal{R}}\right) \\
=\mathrm{lqi}\left(\mathrm{ss}\left(\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}\right), \mathbf{Q}, \mathbf{R}\right)
\boldsymbol{\mathcal{K}}=\begin{bmatrix} \mathbf{K}_1 & \mathbf{K}_2 \end{bmatrix}
El LQI para sistemas LTI
para el caso LTI la situación se simplifica considerablemente
>> \boldsymbol{\mathcal{K}}=\mathrm{lqr}\left(\boldsymbol{\mathcal{A}},\boldsymbol{\mathcal{B}},\boldsymbol{\mathcal{Q}},\boldsymbol{\mathcal{R}}\right) \\
=\mathrm{lqi}\left(\mathrm{ss}\left(\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}\right), \mathbf{Q}, \mathbf{R}\right)
\boldsymbol{\mathcal{K}}=\begin{bmatrix} \mathbf{K}_1 & \mathbf{K}_2 \end{bmatrix}
\mathbb{R}^{m \times n}
\mathbb{R}^{m \times \dim(\mathbf{r})}
El LQI para sistemas LTI
adicionalmente, para el caso LTI la referencia puede variar en el tiempo de "gratis"
aunque el rendimiento es sólo "decente"
>> ie3041_clase10_linear_lqi.m
Gain scheduling
la segunda "mejora" que consideraremos surge de aeronaútica, específicamente de los controladores para aviones comerciales
la segunda "mejora" que consideraremos surge de aeronaútica, específicamente de los controladores para aviones comerciales
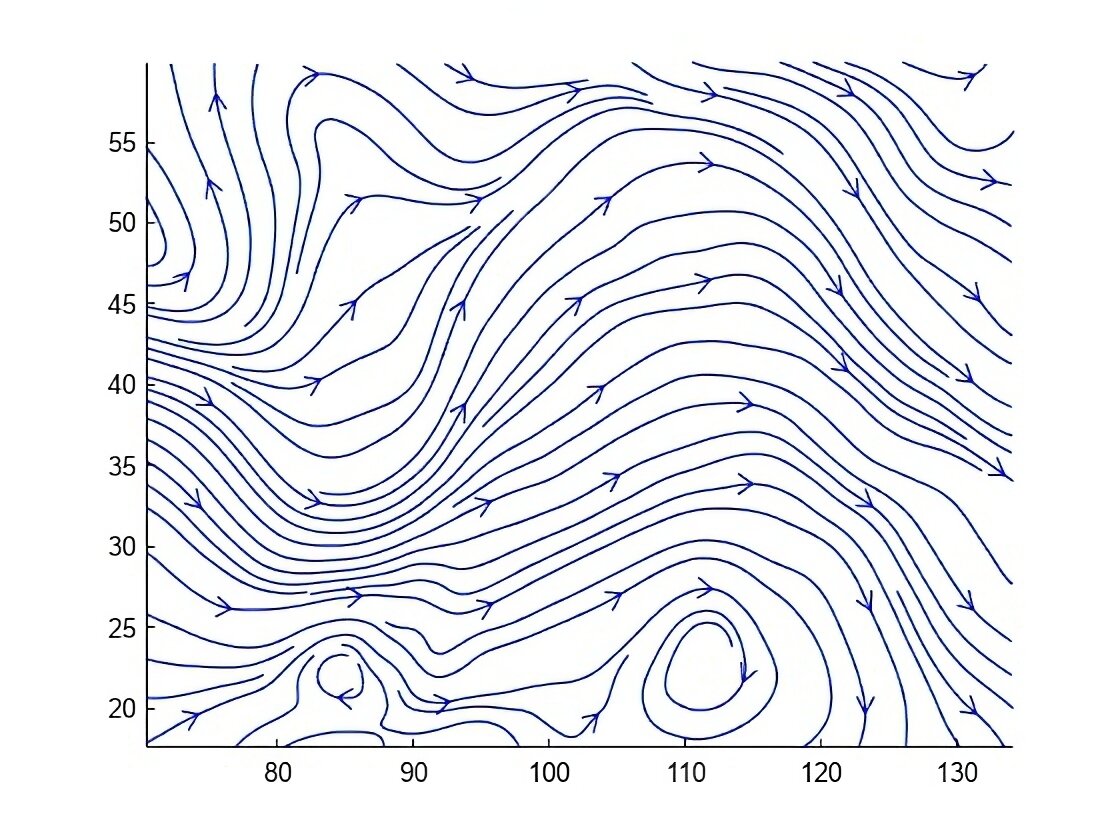
en lugar de tener un sólo controlador local con una amplia región de atracción, propone tener una familia de controladores que representen los modos de operación y hacer una transición entre ellos
1
\mathbf{u}_1\left(\mathbf{x}\right)
1
2
\mathbf{u}_1\left(\mathbf{x}\right)
\mathbf{u}_2\left(\mathbf{x}\right)
1
2
3
4
\mathbf{u}_1\left(\mathbf{x}\right)
\mathbf{u}_2\left(\mathbf{x}\right)
\mathbf{u}_3\left(\mathbf{x}\right)
\mathbf{u}_4\left(\mathbf{x}\right)
1
2
3
4
hard switch (transición discontinua)
1
2
3
4
hard switch (transición discontinua)
el cambio brusco puede desestabilizar al sistema
1
2
3
4
\mathbf{u}\left(\mathbf{x}, \alpha_1\right)
\mathbf{u}\left(\mathbf{x},\alpha_2\right)
\mathbf{u}\left(\mathbf{x},\alpha_3\right)
\mathbf{u}\left(\mathbf{x}, \alpha_4\right)
idea:
1
2
3
4
\mathbf{u}\left(\mathbf{x}, \alpha_1\right)
\mathbf{u}\left(\mathbf{x},\alpha_2\right)
\mathbf{u}\left(\mathbf{x},\alpha_3\right)
\mathbf{u}\left(\mathbf{x}, \alpha_4\right)
idea:
\(\alpha=\) scheduling variable
cambio suave mediante interpolación
Un ejemplo simple de gain scheduling
consideremos dos LQRs linealizados en dos puntos de operación
Un ejemplo simple de gain scheduling
consideremos dos LQRs linealizados en dos puntos de operación
\mathbf{u}_1=-\mathbf{K}_1\left(\mathbf{x}-\mathbf{x}_{1,ss}\right)+\mathbf{u}_{1,ss}
\mathbf{u}_2=-\mathbf{K}_2\left(\mathbf{x}-\mathbf{x}_{2,ss}\right)+\mathbf{u}_{2,ss}
Un ejemplo simple de gain scheduling
consideremos dos LQRs linealizados en dos puntos de operación
\mathbf{u}_1=-\mathbf{K}_1\left(\mathbf{x}-\mathbf{x}_{1,ss}\right)+\mathbf{u}_{1,ss}
\mathbf{u}_2=-\mathbf{K}_2\left(\mathbf{x}-\mathbf{x}_{2,ss}\right)+\mathbf{u}_{2,ss}
\mathbf{u}(\alpha)=(1-\alpha)\mathbf{u}_1+\alpha\mathbf{u}_2
interpolación lineal de ganancias
Un ejemplo simple de gain scheduling
consideremos dos LQRs linealizados en dos puntos de operación
\mathbf{u}_1=-\mathbf{K}_1\left(\mathbf{x}-\mathbf{x}_{1,ss}\right)+\mathbf{u}_{1,ss}
\mathbf{u}_2=-\mathbf{K}_2\left(\mathbf{x}-\mathbf{x}_{2,ss}\right)+\mathbf{u}_{2,ss}
\mathbf{u}(\alpha)=(1-\alpha)\mathbf{u}_1+\alpha\mathbf{u}_2
NOTA: gain scheduling es una metodología, NO una técnica en particular
\alpha(t), \ \alpha \in [0,1]
interpolación lineal de ganancias
Un ejemplo simple de gain scheduling
consideremos dos LQRs linealizados en dos puntos de operación
\mathbf{u}_1=-\mathbf{K}_1\left(\mathbf{x}-\mathbf{x}_{1,ss}\right)+\mathbf{u}_{1,ss}
\mathbf{u}_2=-\mathbf{K}_2\left(\mathbf{x}-\mathbf{x}_{2,ss}\right)+\mathbf{u}_{2,ss}
\mathbf{u}(\alpha)=(1-\alpha)\mathbf{u}_1+\alpha\mathbf{u}_2
\alpha(t), \ \alpha \in [0,1]
interpolación lineal de ganancias
>> ie3041_clase10_stabilize2d_gs.m
Más allá de controladores locales
¿Por qué nuestros controladores lineales han sido sólo "decentes" para el caso no lineal?
¿Por qué nuestros controladores lineales han sido sólo "decentes" para el caso no lineal?
\(\Rightarrow\) al linealizar limitamos a local el alcance de los controladores y nos sometemos a la región de atracción del punto de operación
(incluso si usamos gain scheduling para generar "trayectorias")
¿Por qué nuestros controladores lineales han sido sólo "decentes" para el caso no lineal?
\(\Rightarrow\) al linealizar limitamos a local el alcance de los controladores y nos sometemos a la región de atracción del punto de operación
(incluso si usamos gain scheduling para generar "trayectorias")
¿Podemos hacer algo mejor?
Un ejemplo simple de gain scheduling
consideremos dos LQRs linealizados en dos puntos de operación
\mathbf{u}_1=-\mathbf{K}_1\mathbf{x}
\mathbf{u}_2=-\mathbf{K}_2\mathbf{x}
\mathbf{u}(\alpha)=-\mathbf{K}(\alpha)\mathbf{x}
\mathbf{K}(\alpha)=\mathbf{K}_1(1-\alpha)+\alpha\mathbf{K}_2
NOTA: gain scheduling es una metodología, NO una técnica en particular
\alpha(t), \ \alpha \in [0,1]
(interpolación lineal de ganancias)
IE3041 - Lecture 10 (2025)
By Miguel Enrique Zea Arenales
