IE3036 - Sistemas de Control 1
2do ciclo, 2024
Lección 6: Respuesta en estado transitorio
¿Por qué?
s=\sigma + \jmath\omega \\
s \in \mathbb{C}
G(s)
\mathrm{Re}(s)
\mathrm{Im}(s)
\sigma
\omega
plano \(s\)
recordemos
Y(s)=G(s)U(s) \\
y(t)=\mathcal{L}^{-1}\left\{Y(s)\right\}
y(t)
\ t
y(t)
\ t
respuesta transitoria
(corto plazo)
respuesta estacionaria
(largo plazo)
Sistemas de primer orden
G(s)=\dfrac{1}{s+\sigma}
g(t)=e^{-\sigma t}\mathbf{1}(t)
\mathbf{1}(t)
y(t)=\frac{1}{\sigma}\left(1-e^{-\sigma t}\right)\mathbf{1}(t)
G(s)
(asintóticamente) estable \(\Rightarrow\) único polo real en \(s=-\sigma\) con \(\sigma>0\)
y(t)
\ t
y_{ss}
\sigma_1
\sigma_3<\sigma_2<\sigma_1
\sigma_2
\sigma_3
y(t)
\ t
y_{ss}
\sigma_1
\sigma_3<\sigma_2<\sigma_1
\sigma_2
\sigma_3
\tau
\approx 63\%
constante de tiempo
\tau=\dfrac{1}{\sigma}
\Rightarrow y(\tau)=y_{ss}\left(1-e^{-\sigma(1/\sigma)}\right)
y(\tau)=\left(1-e^{-1}\right)y_{ss}\approx 0.63 y_{ss}
La constante de tiempo es el único parámetro de rendimiento para sistemas de primer orden.
Un parámetro de rendimiento representa a alguna característica (en el tiempo) de la respuesta del sistema pero en función de cantidades en \(\mathcal{L}\).
Sistemas de segundo orden
G(s)=\dfrac{b_0}{s^2+a_1s+a_2}=K\dfrac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2}
forma estándar
\(\zeta\equiv\) factor o coeficiente de amortiguamiento
\(\to\) sub-amortiguado: \(\quad 0<\zeta<1\)
\(\to\) críticamente amortiguado: \(\quad \zeta=1\)
\(\to\) sobre-amortiguado: \(\quad \zeta>1\)
G(s)=\dfrac{b_0}{s^2+a_1s+a_2}=K\dfrac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2}
forma estándar
\(\omega_n\equiv\) frecuencia natural o frecuencia sin amortiguamiento
\(\sigma=\zeta\omega_n\)
\(\omega_d=\omega_n\sqrt{1-\zeta^2}\equiv\) frecuencia amortiguada
G(s)=\dfrac{b_0}{s^2+a_1s+a_2}=K\dfrac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega_n^2}
forma estándar
se asume (asintóticamente) estable con polos en
s^2+2\zeta\omega_n s+\omega_n^2=0
\Rightarrow s=-\sigma\pm\jmath\omega_d
\mathrm{Re}(s)
\mathrm{Im}(s)
\sigma
\omega_d
-\omega_d
\omega_n
\theta
\theta=\sin^{-1}(\zeta)
\mathbf{1}(t)
y(t)=\left( 1-\dfrac{\omega_n}{\sqrt{1-\zeta^2}}e^{-\sigma t}\sin(\omega_d t) \right)\mathbf{1}(t)
G(s)
y(t)
y(t)
\ t
y_{ss}
y(t)
\ t
y_{ss}
10\%
90\%
t_r
tiempo de subida
y(t)
\ t
y_{ss}
t_p
M_p
tiempo pico
% de overshoot o
sobreoscilación / sobreelevación
y(t)
\ t
y_{ss}
-\epsilon
+\epsilon
t_s
tiempo de asentamiento o establecimiento
\(\epsilon\sim\) 5%, 2%, 1%
y(t)
\ t
y_{ss}
-\epsilon
+\epsilon
10\%
90\%
t_s
t_r
t_p
M_p
\(t_r, t_s\) y \(M_p\) como parámetros de rendimiento para sistemas de segundo orden
t_r \approx \dfrac{1.8}{\omega_n}
t_p = \dfrac{\pi}{\omega_d}
M_p=e^{-\zeta\pi/\sqrt{1-\zeta^2}} \times 100\%
M_p=f(\zeta)
t_s = \dfrac{4.6}{\sigma}, \quad \epsilon=1\%
t_s = \dfrac{3.9}{\sigma}, \quad \epsilon=2\%
t_s = \dfrac{3.0}{\sigma}, \quad \epsilon=5\%
S = stepinfo(sys)
S = stepinfo(y, t, yfinal)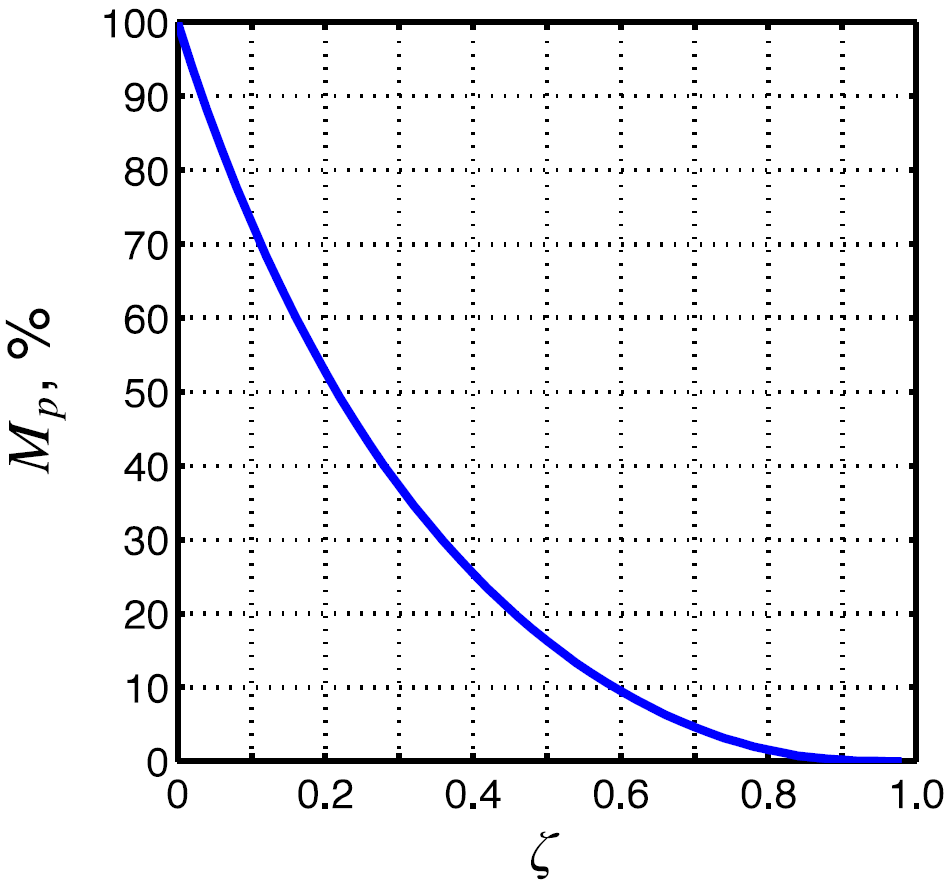
M_p=f(\zeta)
¿Y si empleáramos los parámetros para evaluar en lugar de describir?
¿Cuál es la función de transferencia de un sistema que presente un \(t_r\approx0.5 \text{ s}\) y un \(M_p\approx10\%\)?
Ejercicio 1
Ejercicio 1
wn = 3.6;
zeta = 0.6;
G = tf(wn^2, [1, 2*zeta*wn, wn^2])¿Cuál es la función de transferencia de un sistema que presente un \(t_r\approx0.5 \text{ s}\) y un \(M_p\approx10\%\)?
Regiones de diseño
\mathrm{Re}(s)
\mathrm{Im}(s)
\omega_n \ge \dfrac{1.8}{t_r}
\omega_n
región donde se cumple con los requerimientos
t_r \le \text{spec.}
\mathrm{Re}(s)
\mathrm{Im}(s)
\zeta \ge f^{-1}\left(M_p\right)
\theta
\theta=\sin^{-1}(\zeta)
M_p \le \text{spec.}
\mathrm{Re}(s)
\mathrm{Im}(s)
\sigma \ge \dfrac{4.6}{t_s}
\sigma
(\epsilon=1\%)
t_s \le \text{spec.}
\mathrm{Re}(s)
\mathrm{Im}(s)
combinando todas las regiones
el sistema cumple con todos los requerimientos
Ejemplo: Dibuje la región de diseño que cumpla con las siguientes especificaciones en el dominio de tiempo.
t_r\le0.6 \text{ s} \quad M_p\le10\% \quad t_s\le3 \text{ s @ } 1\%
¿Qué pasa cuando los sistemas tienen ceros o son de orden superior?
- \(+1\) polo en el LHP incrementa el \(t_r\) si se encuentra dentro de un factor de \(\approx 4\) de la parte real de los polos dominantes.
- \(+1\) cero en el LHP incrementa el \(M_p\) si se encuentra dentro de un factor de \(\approx 4\) de la parte real de los polos dominantes.
- \(+1\) cero en el RHP disminuye el \(M_p\) pero puede causar que la respuesta inicie en la dirección incorrecta \(\Rightarrow\) delay.
>> clase6_aproximaciones2dorden.m
\mathrm{Re}(s)
\mathrm{Im}(s)
\mathrm{Re}(s)
\mathrm{Im}(s)
\(\approx\) sistema de 1er orden
\real(p_i)\le 4 \real(p_\textrm{dom})
\(\approx\) sistema de 2do orden
lejos de \(\jmath\omega\)
polos insignificantes
cerca de \(\jmath\omega\)
polos dominantes
y(t)
\ t
y_{ss}
delay
¿Cuál es un modelo de segundo orden que aproxima al sistema?
Ejercicio 2
G(s)=\dfrac{175.2s+876}{s^5+24s^4+215s^3+820s^2+1214s+876}
¿Cuál es un modelo de segundo orden que aproxima al sistema?
Ejercicio 2
G(s)=\dfrac{175.2s+876}{s^5+24s^4+215s^3+820s^2+1214s+876}
G = tf([175.2, 876], [1, 24, 215, 820, 1214, 876])
Gapprox = zpk([], [-1+1i, -1-1i], 2)
step(G, Gapprox)IE3036 - Lecture 6 (2025)
By Miguel Enrique Zea Arenales
