Introducción y
Lección 1: Sistemas LTI en Tiempo Continuo
IE3036 - Sistemas de Control 1
2do ciclo, 2025
Programa de la iniciativa académica
Resumen del contenido
Distribución de nota
Lecturas semanales y comprobaciones
Tareas y ejercicios sugeridos
Referencias bibliográficas
Canvas y otros detalles adicionales
+
-
referencia
planta | sistema: ¿Qué quiero controlar?
referencia: ¿Qué quiero que haga el sistema?
salida: ¿Qué está haciendo el sistema?
sensor: ¿Cómo obtengo (o mido) lo que está haciendo el sistema?
controlador: ¿Qué debe hacerse para que el sistema haga lo que quiero que haga?
+
-
referencia
planta
sensor
controlador
salida
retroalimentación negativa
+
-
referencia
planta
sensor
controlador
salida
retroalimentación negativa
entrada
\mathcal{G}
u(t)
y(t)
teoría de sistemas dinámicos
=\mathcal{G}\left\{u(t)\right\}
sistema
parámetro concentrado
parámetro distribuido
determinístico
estocástico
tiempo continuo
tiempo discreto
tiempo continuo
lineal
no lineal
invariante en el tiempo
variante en el tiempo
Sistemas LTI (Linear Time Invariant)
Sistemas LTI (en tiempo continuo)
Recordemos:
- Linealidad
- Homogeneidad
- Superposición
- Invarianza en el tiempo
¿Son sistemas LTI?
y(t)=4u(t)
y(t)=3u(t)+5
y(t)=u(2t)
planta
salida
entrada
\mathcal{G}
u(t)
y(t)
¿Por qué sistemas LTI?
Engineered systems
física
\ddot{x}+\dfrac{b}{m}\dot{x}=\dfrac{1}{m}u
EDO lineal de coeficientes constantes
x
b\dot{x}
u
mecánica
J\ddot{\theta}=\tau
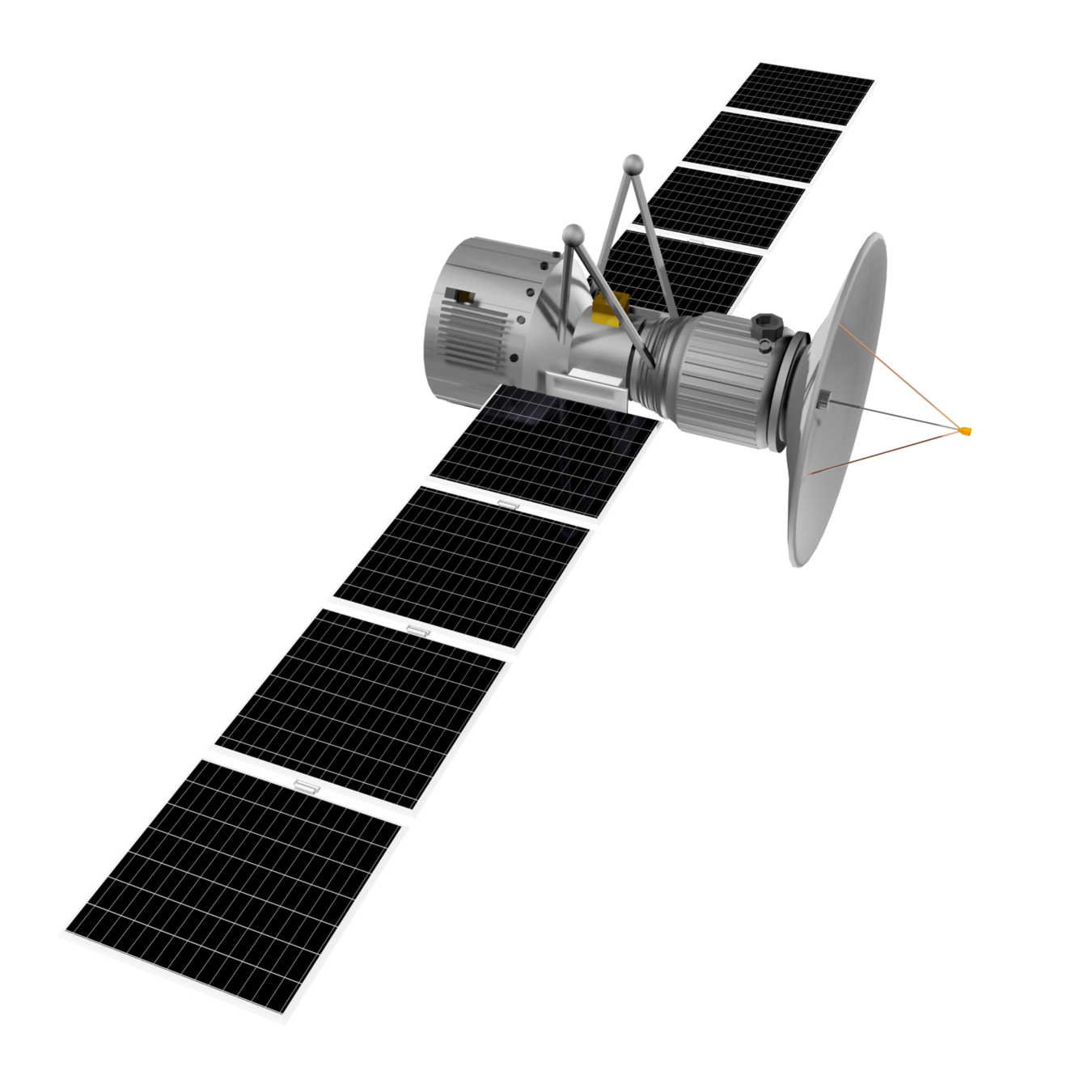
EDO lineal de coeficientes constantes
\tau
\theta
electrónica
\dot{v}_o=-\dfrac{1}{RC}v_i
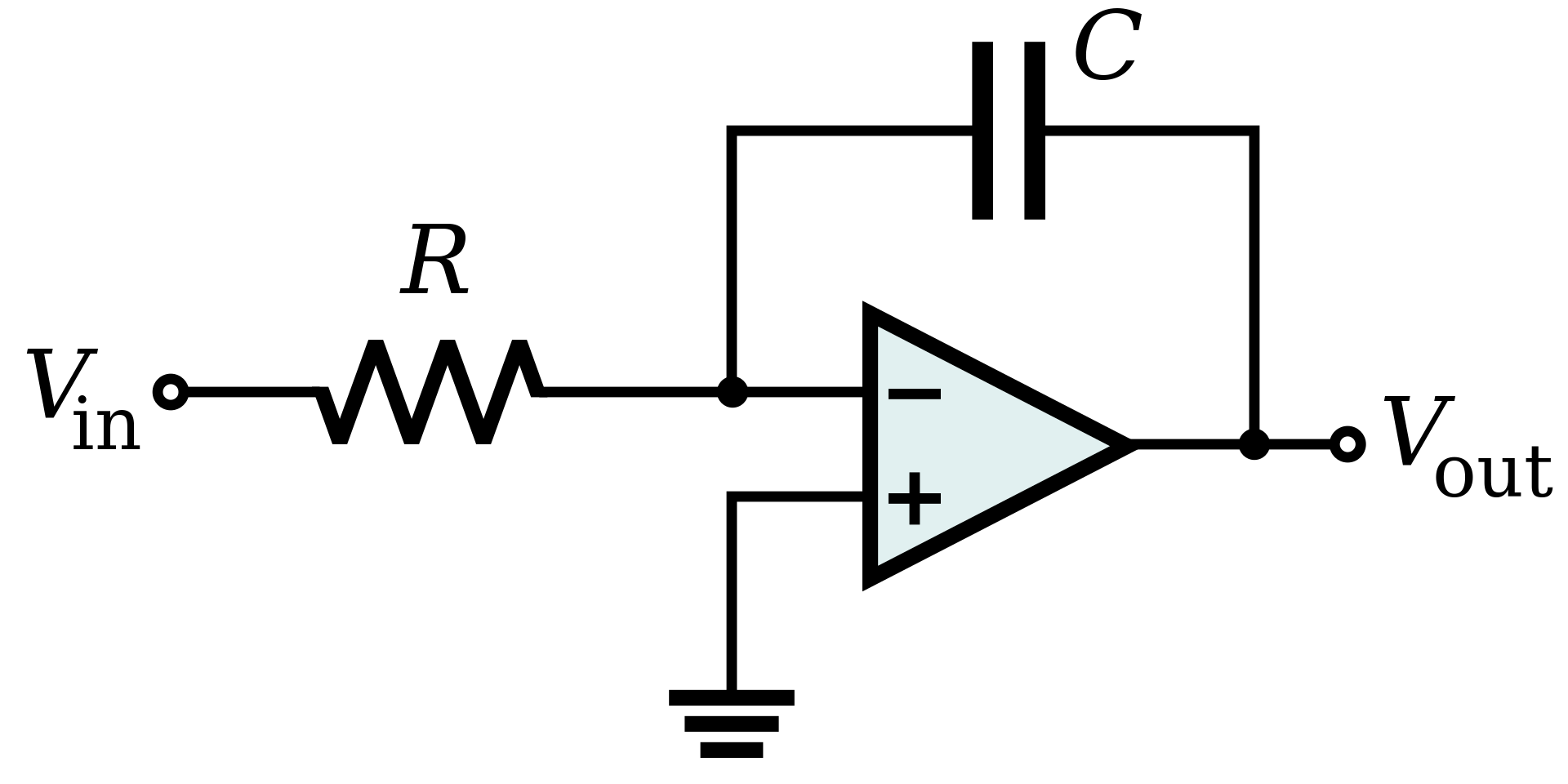
EDO lineal de coeficientes constantes
TODO sistema LTI puede expresarse como una EDO lineal de coeficientes constantes que relaciona a su salida con su entrada.
Modelado lineal
Aproximación lineal de componentes
Métodos de transformadas
Respuestas a señales estándar
\mathcal{G}
u(t)
y(t)
señal (de prueba) estándar
respuesta típica
escalón
impulso
Escalón unitario
\mathcal{G}
u(t)
y(t)
respuesta al escalón
\mathbf{1}(t)=\begin{cases} 0 & \text{ si } t<0 \\ 1 & \text{ si } t\ge0 \end{cases}
t
\mathbf{1}(t)
Impulso unitario | delta de Dirac
\mathcal{G}
u(t)
y(t)
respuesta impulsional
\delta(t)=\begin{cases} ``\infty" & \text{ si } t=0 \\ 0 & \text{ si } t\ne0 \end{cases}
t
\delta(t)
g(t)
y(t)=\displaystyle\int_{-\infty}^{\infty}u(\tau)g(t-\tau)d\tau \equiv u(t) * g(t)
Respuesta en el tiempo de un sistema LTI
Y(s)=G(s)U(s)
Respuesta de un sistema LTI (Laplace)
G(s)=\dfrac{Y(s)}{U(s)}
Función de transferencia
G(s)
u(t)
y(t)=\mathcal{G}\left\{u(t)\right\}
planta
entrada
salida
U(s)
Y(s)=G(s)U(s)
IE3036 - Lecture 1 (2025)
By Miguel Enrique Zea Arenales
