Prisoners' Dilemma
Cooperate
Cooperate
1
2
Defect
Defect
2
2
3
0
0
3
1
1
There's only one Nash equilibrium of this game.
Does it feel right? Do you live in a world in which nobody ever cooperates?
pollev.com/chrismakler
Repeated Games
and Collusion
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 11
Today's Agenda
Part 1: Discrete Strategies
Part 2: Continuous Strategies
Finitely-repeated games
Evaluating infinite payoffs
Infinitely-repeated games
Collusion in Cournot Duopoly
Big Ideas
The ability to do so relies on
the ability to credibly promise/threaten something in the future,
and a high enough value placed on future payoffs
In ongoing relationships,
you can achieve things you cannot achieve in one-shot games.
What are we modeling?
-
Players who have ongoing relationships:
- Delta Airlines and American Airlines
- Managers and employees
- Spouses, roommates, friends
- Members of political parties
- Decisions they make have an immediate impact but also an impact on the relationship.
- How much greater is GDP because of the level of social capital (trust and other investments in relationships) is higher? How much worse off are we if that trust is eroded?
Finitely Repeated Games
-
Suppose there is some stage game G, which is repeated for T periods, with the payoffs being the sum of the payoffs in each period.
-
Trivial result: it is always a SPNE if a NE is played in every period.
-
Nontrivial result: there may be SPNE in which non-NE strategy profiles are played in early periods.
-
Key insight: this requires multiple Nash equilibria, which gives the ability to credibly promise a reward in the last period
pollev.com/chrismakler
1
2
A
B
X
Y
Z
4
0
1
2
3
1
0
4
0
0
0
0
If the following game is just played once, what are the Nash Equilibria?
1
2
A
B
X
Y
Z
If the following game is just played once, what are the Nash Equilibria?
4
0
1
2
3
1
0
4
0
0
0
0
If the following game is just played once, what are the Nash Equilibria?
A
Z
B
Y
1
2
A
B
X
Y
Z
If the following game is just played once, what are the Nash Equilibria?
4
0
1
2
3
1
0
4
0
0
0
0
What are the strategy spaces of the two players if the game is played twice?
A
Z
B
Y
What to do in the first period
What to do after every possible outcome of the first period.
1
2
A
B
X
Y
Z
4
0
1
2
3
1
0
4
0
0
0
0
What to do in the first period
What to do after every possible outcome of the first period.
Player 1
Player 2
A
B
X
Y
Z
A
B
X
Y
Z
Suppose the game is played twice, and the payoffs are the sum of the payoffs in each period.
A
A
B
B
B
B
B
If (A,X) was played, play A.
If anything else was played, play B.
What is B's best response to this stragey for A?
If (A,X) was played, play Z.
If anything else was played, play Y.
Z
Y
Y
Y
Y
Y
Start with the second stage: best to play the best response
from the stage game to whatever A chooses
1
2
A
B
X
Y
Z
4
0
1
2
3
1
0
4
0
0
0
0
What to do in the first period
What to do after every possible outcome of the first period.
Player 1
Player 2
A
B
X
Y
Z
A
B
X
Y
Z
A
A
B
B
B
B
B
If (A,X) was played, play A.
If anything else was played, play B.
If (A,X) was played, play Z.
If anything else was played, play Y.
Z
Y
Y
Y
Y
Y
Given all of this, what should player 2 play in the first stage?
?
1
2
A
B
X
Y
Z
4
0
1
2
3
1
0
4
0
0
0
0
Player 1
Player 2
Play A in the first period.
If (A,X) was played, play A.
If anything else was played, play B.
If (A,X) was played, play Z.
If anything else was played, play Y.
?
Suppose player 2 plays Z.
In the first period, they get 4. Yay!
In the second period, since (A,X) was not played, player 1 plays B and player 2 plays Y,
and player 2 gets a payoff of 1.
Sum of payoffs = 4 + 1 = 5
Suppose player 2 plays X.
In the first period, they get 3. OK!
In the second period, since (A,X) was played, player 1 plays A and player 2 plays Z,
and player 2 gets a payoff of 4.
Sum of payoffs = 3 + 4 = 7
X
1
2
A
B
X
Y
Z
4
0
1
2
3
1
0
4
0
0
0
0
Player 1
Player 2
Play A in the first period.
If (A,X) was played, play A.
If anything else was played, play B.
If (A,X) was played, play Z.
If anything else was played, play Y.
X
What's going on?
There are two NE in this game; one is better for player 2 by 3 points.
Player 1 can't promise to play non-NE strategies in the second stage, but they can offer to "reward" player 2 by coordinating on the one that's better for them if player 2 plays X in the first period.
This doesn't hurt player 2 too much, so they go along with it!
Infinitely Repeated Games
Infinitely Repeated Games
- A stage game G is repeated an infinite number of times.
- Can't just sum up the payoffs (would be infinite!)
- Approach: use discounting, like we did in week 2
V(\pi_0,\pi_1,\pi_2,\pi_3, \cdots) = \pi_0 + \delta \pi_1 + \delta^2 \pi_2 + \delta^3 \pi_3 \cdots
V(x) = x + \delta x + \delta^2 x + \delta^3 x + \cdots
The present value of a stream of payoffs
(\(\pi_0\) now, \(\pi_1\) in the next period, \(\pi_2\) two periods from now, etc)
may be given by the infinite sum
The present value of a stream of payoffs of \(x\) in every period is:
V(x) = x + \delta [x + \delta x + \delta^2 x + \cdots]
Factor out \(\delta\) from the second and following terms:
What is this expression?
V(x) = x + \delta V(x)
(1-\delta)V(x) = x
V(x) = {x \over 1 - \delta}
The present value of a stream of payoffs of \(x\) in every period is:
\displaystyle{V(x,x,x,x, \cdots) = {x \over 1 - \delta}}
The present value of a stream of payoffs of \(z\) in every period,
starting next period, is:
\displaystyle{V(0,z,z,z, \cdots) = \delta \left[{z \over 1 - \delta}\right]}
The present value of getting
payoff \(y\) now, and then payoff \(z\) in every period thereafter, is:
\displaystyle{V(y,z,z,z, \cdots) = y + \delta \left[{z \over 1 - \delta}\right]}
Write these formulas down!
Strategies in Infinitely Repeated Games
- Strategies must specify what to do in each period,
as a function of the history of all previously taken actions - We often group action histories to make strategy description simpler:
SPNE in Infinitely Repeated Games
- Can't do backward induction!
- Instead: "guess a strategy profile, and "check" that it is a Subgame Perfect Nash Equilibrium
- A simple SPNE: play the Nash Equilibrium of the stage game in every period, for any history
- Can we have a SPNE
in which there is cooperation?
‟Grim Trigger" Strategy (a.k.a. ‟Grudger")
Suppose your opponent is playing this strategy. Is playing this strategy a best response?
Cooperate
Cooperate
1
2
Defect
Defect
2
2
3
0
0
3
1
1
What is your payoff if you too play Grim Trigger?
What is your most profitable deviation?
Get a payoff of 2 in every period.
\displaystyle{V(2,2,2,2, \cdots) = {2 \over 1 - \delta}}
Get a payoff of 3 once, then 1 in every period.
\displaystyle{V(3,1,1,1, \cdots) = 3 + \delta \left[{1 \over 1 - \delta}\right]}
‟Grim Trigger" Strategy (a.k.a. ‟Grudger")
Suppose your opponent is playing this strategy. Is playing this strategy a best response?
What is your payoff if you too play Grim Trigger?
What is your most profitable deviation?
\displaystyle{V(2,2,2,2, \cdots) = {2 \over 1 - \delta}}
\displaystyle{V(3,1,1,1, \cdots) = 3 + \delta \left[{1 \over 1 - \delta}\right]}
When is GT a best response to GT?
\displaystyle{{2 \over 1 - \delta} > 3 + \delta \left[{1 \over 1 - \delta}\right]}
Multiply both sides by \(1 - \delta\):
2 > 3(1-\delta) + \delta
2\delta > 1
\delta > {1 \over 2}
If people are sufficiently patient (value future payoffs highly enough), then cooperation can be sustained using a "grim trigger" strategy.
Collusion
What is firm 2's best response function?
P(q_1,q_2) = 14 - (q_1+q_2)
c_2(q_2) = 2q_2
\pi_2(q_2) = P(q_1 + q_2)q_2 - c_2(q_2)
= (14 - q_1 - q_2)q_2 - 2q_2
= 14q_2 - q_1q_2 - q_2^2 - 2q_2
\pi'_2(q_2) = 14-q_1 - 2q_2 - 2 = 0
q_2^* = BR_2(q_1) = 6-\frac{1}{2}q_1
\text{total revenue}
\text{total cost}
\text{marginal revenue}
\text{marginal cost}
2
P
P(q_2|q_1) = 14-q_1 - q_2
MR(Q) = 14-q_1 - 2q_2
MC(q_2) = 2
6-\frac{1}{2}q_1
14-q_1
q_2
"Firm 2's Residual Demand Curve"
Firm 2's "best response function"
Cournot Best Response Functions
BR_1(q_2) = 6 - {1 \over 2}q_2
Firm 1's
best response function
BR_2(q_1) = 6 - {1 \over 2}q_1
Firm 2's
best response function
q_1
q_2
BR_1(q_2) = 6 - {1 \over 2}q_2
BR_2(q_1) = 6 - {1 \over 2}q_1
Nash equilibrium (a.k.a. Cournot equilibrium) is a pair of quantities \((q_1,q_2)\) such that
q_1 = BR_1(q_2)
q_2 = BR_2(q_1)
Profits in Cournot Equilibrium
In Cournot equilibrium, \(q_1 = q_2 = 4\).
\text{Combined profits = }\underbrace{P(q_1,q_2)q_1 - c(q_1)}_\text{Firm 1's profit} + \underbrace{P(q_1,q_2)q_2 - c(q_2)}_\text{Firm 2's profit}
= (14 - q_1 - q_2)q_1 - 2q_1 + (14 - q_1 - q_2)q_2 - 2q_2
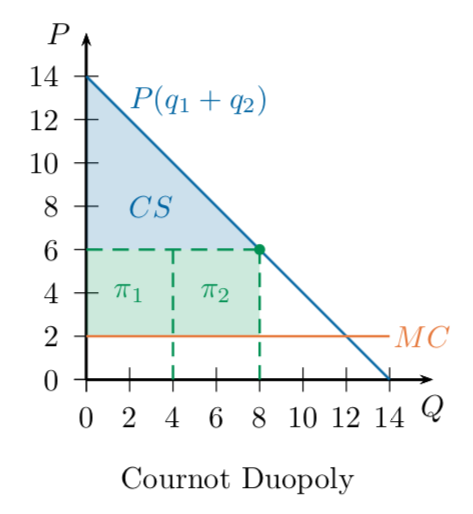
Is this the best they could do? Suppose they each produced some amount \(q\).
What value of \(q\) would maximize their combined profits?
\text{Combined profits if they each produce 4 }= \underbrace{(14 - 4 - 4)4 - 2 \times 4}_{\pi_1(4,4) = 16}
+ \underbrace{(14 - 4 - 4)4 - 2\times 4}_{\pi_2(4,4) = 16}
\text{Combined profits if they each produce }q= \underbrace{(14 - q - q)q - 2q}_{\pi_1(q,q)} + \underbrace{(14 - q - q)q - 2q}_{\pi_2(q,q)}
\text{Combined profits if they each produce 4 }= \underbrace{(14 - 4 - 4)4 - 2 \times 4}_{\pi_1(4,4) = 16}
+ \underbrace{(14 - 4 - 4)4 - 2\times 4}_{\pi_2(4,4) = 16}
\text{Combined profits if they each produce }q= \underbrace{(14 - q - q)q - 2q}_{\pi_1(q,q)} + \underbrace{(14 - q - q)q - 2q}_{\pi_2(q,q)}
= 2[(14 - q - q)q - 2q]
= 2[14q - 2q^2 - 2q]
= 2[12q - 2q^2]
= 24q - 4q^2
Take derivative, set it equal to zero:
24 - 8q = 0
\Rightarrow q^* = 3
\text{Combined profits if they each produce 3 }= \underbrace{(14 - 3 - 3)3 - 2 \times 3}_{\pi_1(3,3) = 18} + \underbrace{(14 - 3 - 3)3 - 2\times 3}_{\pi_2(3,3) = 18}
\text{Combined profits if they each produce 4 }= \underbrace{(14 - 4 - 4)4 - 2 \times 4}_{\pi_1(4,4) = 16}
+ \underbrace{(14 - 4 - 4)4 - 2\times 4}_{\pi_2(4,4) = 16}
\text{Combined profits if they each produce 3 }= \underbrace{(14 - 3 - 3)3 - 2 \times 3}_{\pi_1(3,3) = 18} + \underbrace{(14 - 3 - 3)3 - 2\times 3}_{\pi_2(3,3) = 18}
But...if the other firm was going to produce 3, what should you produce?
BR_i(q_{-i}) = 6 - {1 \over 2}q_{-i}
BR_i(3) = 6 - {1 \over 2}3 = 4.5
\pi_i(4.5,3) = 20.25
COLLUSION
If both produce 3...
BETRAYAL
If you produce 4.5 while they produce 3...
NASH EQUILIBRIUM
If both produce 4
x = 18
y = 20.25
z = 16
\displaystyle{V(x,x,x,x, \cdots) = {x \over 1 - \delta}}
\displaystyle{V(y,z,z,z, \cdots) = y + \delta \left[{z \over 1 - \delta}\right]}
If both firms play a "grim trigger" strategy, when can they sustain collusion?
pollev.com/chrismakler
COLLUSION
If both produce 3...
BETRAYAL
If you produce 4.5 while they produce 3...
NASH EQUILIBRIUM
If both produce 4
x = 18
y = 20.25
z = 16
\displaystyle{V(18,18,18, \cdots) = {18 \over 1 - \delta}}
\displaystyle{V(20.25,16,16, \cdots) = 20.25 + \delta \left[{16 \over 1 - \delta}\right]}
\displaystyle{{18 \over 1 - \delta} > 20.25 + \delta \left[{16 \over 1 - \delta}\right]}
18 > 20.25(1-\delta) + 16\delta
4.25\delta > 2.25
\delta > {2.25 \over 4.25} = {9 \over 17} \approx 0.53
What did we show this week?
- Tuesday: some Nash equilibria are not subgame perfect, because they depend on non-credible threats or promises.
- Today: some non-Nash outcomes of a stage game (e.g. cooperation in a Prisoners' Dilemma) can be sustained if the players have an ongoing relationship.
- Sunday: homework for this week due
- Next Tuesday: review of game theory thus far
- Tuesday night: you may hand in practice exam questions for credit; that's what "Week 7 homework is"
- Next Thursday: Midterm 2
Econ 51 | 11 | Repeated Games
By Chris Makler
Econ 51 | 11 | Repeated Games
Sequential Games of Complete and Perfect Information
