Introduction to
Game Theory
Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 7
pollev.com/chrismakler
Name a company.
- Motivation: why game theory?
- Overview of the next 6 weeks
- Components of a game
- The extensive form (ch. 2)
- Strategies and the normal form (ch. 3)
- Beliefs, mixed strategies, and expected payoffs (ch. 4)
Today's Agenda
- Up until now: agents only (really) interact with "the market" via prices
- In real life, people, firms, countries ("players") interact with each other.
- Our economic lives are interconnected: our well-being doesn't depend only on our own actions, but on the actions taken by others
- Questions:
- OPTMIZATION: How do you operate in a world like this?
- EQUILIBRIUM: What is our notion of "equilibrium" in a world like this, and how is it different from competitive equilibrium?
- POLICY: Given how people behave in strategic settings, how can we design "mechanisms" to achieve policy goals?
Motivation
- The branch of economics that studies strategic interactions between economic agents.
- Everyone's payoffs depend on the actions chosen by all agents
- To "play the game," each agent thinks strategically about how the other agents are playing
Game Theory
-
Industrial organization: situations where a few firms dominate the market,
and each firm's decisions affect others -
Political economy: campaigning, governing, international diplomacy,
provision of public goods - Contract negotiations: incentive structures, credible threats, negotiating over price
- Interpersonal relationships: team dynamics, division of chores within a family
Applications
-
Today: Setup of the Model
- Lecture: Notation and terminology [Watson Ch. 1-5]
- Section: Review of monopoly profit maximization (HW ex. 4.3, 4.4)
-
Week 5: Equilibrium in a One-Shot Game
- Tuesday: Dominance, best response, rationalizability [Watson Ch. 6-7]
- Thursday: Nash Equilibrium [Watson Ch. 9-11]
-
Week 6: Dynamic Games
- Tuesday: Dynamic games & subgame perfection [Watson Ch. 14-15]
- Thursday: Repeated games & collusion [Watson Ch. 22-23]
- Week 7: Applications, Review, and Midterm II
Next Three Weeks:
Games of Complete & Perfect Information
- Players: who is playing the game?
- Actions: what can the players do at different points in the game?
- Information: what do the players know when they act?
- Outcomes: what happens, as a function of all players' choices?
- Payoffs: what are players' preferences over outcomes?
Components of a Game
- Outcomes: what happens, as a function of all players' choices?
- Payoffs: what are players' preferences over outcomes?
1
2
1
1
,
0
0
,
1
1
,
0
0
,
Left
Right
Left
Right
1
2
Left
Right
Left
Right
Both OK
Both OK
Crash
Crash
Outcomes
Two bikers approach on an unmarked bike path.
Payoffs
i = \text{Player }i
-i = \text{Player(s) other than }i
\text{Example: Consider a strategy profile for four players }s = (s_1, s_2, s_3, s_4)
\text{If we consider player 2, then }s_i = s_2 \text{ and } s_{-i}=(s_1, s_3, s_4)
u_i(s_i,s_{-i}) = \text{Player $i$'s utility from playing $s_i$ when others play $s_{-i}$}
Notation Convention
The Extensive Form
(Watson, Chapter 2)
Extensive Form
Nodes:
Branches:
Initial node: where the game begins
Decision nodes: where a player makes a choice; specifies player
Terminal nodes: where the game ends; specifies outcome
Individual actions taken by players; try to use unique names for the same action (e.g. "left") taken at different times in the game
Information sets:
Sets of decision nodes at which the decider and branches are the same, and the decider doesn't know for sure where they are.
A "tree" representation of a game.
Example: Gift-Giving
She chooses to give one of three gifts:
X, Y, or Z.
1
X
Y
Z
Player 1 makes the first move.
Initial node
Player 1's actions at her decision node
(and decision node)
Example: Gift-Giving
Twist: Gift X is unwrapped,
but Gifts Y and Z are wrapped.
(Player 1 knows what they are,
but player 2 does not.)
After each of player 1's moves,
player 2 has the move: she can either accept the gift or reject it.
2
Accept X
Reject X
2
1
X
Y
Z
We represent this by having an information set connecting
player 2's decision nodes
after player 1 chooses Y or Z.
2
2
Player 2's actions
Player 2's decision nodes
Information set
Accept Y
Reject Y
Accept Z
Reject Z
Also: player 2 cannot make her action contingent on Y or Z; her actions must be "accept wrapped" or "reject wrapped"
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
Example: Gift-Giving
After player 2 accepts or rejects the gift, the game ends (terminal nodes) and payoffs are realized.
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
Accept X
Reject X
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
Terminal Nodes
Player 1's payoffs
Player 2's payoffs
In this game, both players get a payoff of
0 if any gift is rejected,
1 if gift X is accepted, and
2 if gift Y is accepted.
If gift Z is accepted, player 1 gets a payoff of 3, but player 2 gets a payoff of –1.
Strategies and the Normal Form
(Watson, Chapter 3)
Strategies and Strategy Spaces
A strategy is a complete, contingent plan of action for a player in a game.
This means that every player
must specify what action to take
at every decision node in the game tree!
A strategy space is the set of all strategies available to a player.
Strategies & Strategy Spaces
Player 1 has a single decision:
which gift to give (X, Y, or Z).
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
Accept X
Reject X
Accept Wrapped
Reject Wrapped
Accept Wrapped
Reject Wrapped
Player 2 might have to make one of two decisions: accept or reject gift X,
and accept or reject a wrapped gift.
Let's abbreviate these as A/R and A'/R'.
A
R
S_1 = \{X,Y,Z\}
S_2 = \{AA', AR', RA', RR'\}
A'
R'
A'
R'
Then player 2's strategy space is
Therefore player 1's strategy space is
Strategy Profiles
A strategy profile \(s = (s_1,s_2)\) is a vector showing which strategy from their strategy space is chosen by each player.
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
A
R
S_1 = \{X,Y,Z\}
S_2 = \{AA', AR', RA', RR'\}
A'
R'
A'
R'
s_1 = Z
s_2 = AR'
The outcome of this is that gift Z is given and rejected, and both players receive a payoff of 0.
\text{Example: }s = (Z, AR')
Note: the strategy profile specifies which action is taken at every decision node!
Notation
Strategy for player \(i\):
Strategy space for player \(i\):
S_1 = \{X,Y,Z\}
s_1 = Z
Strategy profile:
s_i
S_i
(s_1, s_2, ..., s_n)
S_2 = \{AA', AR', RA', RR'\}
s_2 = AR'
(\ \ \ ,\ \ \ \ \ \ \ )
Z
AR'
(a complete, contingent plan for how player \(i\) will move)
(set of all possible strategies for player \(i\))
(list of strategies chosen by each player \(i = 1,2,...,n\))
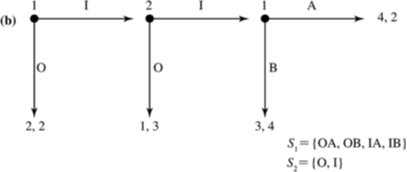
Player 1's Strategy Space:
Player 2's Strategy Space:
\{
\}
\{
\}
A,P,O
A,P
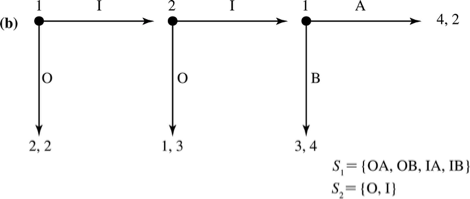
pollev.com/chrismakler
How many strategies does player 1 have
in her strategy space?
Player 1's Strategy Space:
Player 2's Strategy Space:
Continuous Strategies
Strategy for player \(i\):
Strategy space for player \(i\):
S_1 = \mathbb{R}_+
q_1 = 6
Strategy profile:
s_i
S_i
(q_1, q_2)
S_2 = \mathbb{R}_+
q_2 = 3
(\ \ \ ,\ \ \ )
6
3
(set of all possible strategies for player \(i\))
(list of strategies chosen by each player \(i\))
Payoffs for both players, as a function of what strategies are played
\pi_1(q_1,q_2) = 12q_1 - q_1^2 - q_1q_2
\pi_2(q_1,q_2) = 12q_2 - q_2^2 - q_1q_2
Suppose two firms each simultaneously choose a quantity \(q_i\) to produce.
Normal-Form Game
List of players: \(i = 1, 2, ..., n\)
Strategy spaces for each player, \(S_i\)
Payoff functions for each player \(i: u_i(s)\),
where \(s = (s_1, s_2, ..., s_n)\) is a strategy profile
listing each player's chosen strategy.
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
A
R
S_1 = \{X,Y,Z\}
S_2 = \{AA', AR', RA', RR'\}
A'
R'
A'
R'
\(X\)
\(AA'\)
1
2
\(AR'\)
\(RA'\)
\(RR'\)
\(Y\)
\(Z\)
Normal Form Representation
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
A
R
S_1 = \{X,Y,Z\}
S_2 = \{AA', AR', RA', RR'\}
A'
R'
A'
R'
\(X\)
\(AA'\)
1
2
\(AR'\)
\(RA'\)
\(RR'\)
\(Y\)
\(Z\)
0
0
,
Normal Form Representation
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
A
R
S_1 = \{X,Y,Z\}
S_2 = \{AA', AR', RA', RR'\}
A'
R'
A'
R'
\(X\)
\(AA'\)
1
2
\(AR'\)
\(RA'\)
\(RR'\)
\(Y\)
\(Z\)
0
0
,
3
–1
,
Normal Form Representation
1
0
1
0
2
0
2
0
3
0
–1
0
2
2
1
X
Y
Z
,
,
,
,
,
,
A
R
S_1 = \{X,Y,Z\}
S_2 = \{AA', AR', RA', RR'\}
A'
R'
A'
R'
\(X\)
\(AA'\)
1
2
\(AR'\)
\(RA'\)
\(RR'\)
\(Y\)
\(Z\)
1
1
,
1
1
,
0
0
,
0
0
,
2
2
,
0
0
,
2
2
,
0
0
,
3
–1
,
0
0
,
3
–1
,
0
0
,
Normal Form Representation
Normal Form Representation
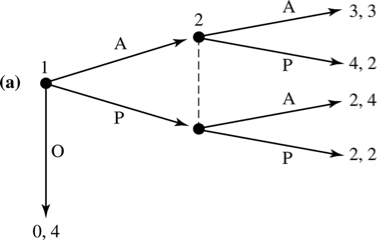
\(OA\)
\(I\)
1
2
\(O\)
\(OB\)
\(IA\)
\(IB\)
2
2
,
2
2
,
4
2
,
3
4
,
2
2
,
2
2
,
1
3
,
1
3
,
Normal Form Representation
\(A\)
\(C\)
1
2
\(D\)
\(B\)
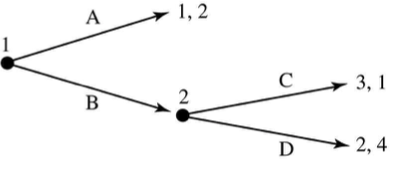
\(A\)
\(C\)
1
2
\(D\)
\(B\)
1
2
,
3
1
,
1
2
,
2
4
,
3
1
,
2
4
,
1
2
,
1
2
,
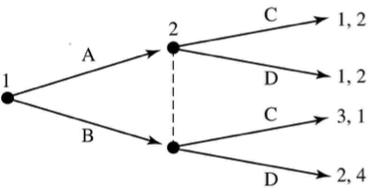
Relationship between Normal-Form
and Extensive-Form Games
Both include the players, strategies, and payoffs.
The extensive form also includes information
on timing and information.
We usually use the normal form for
static (simultaneous-move) games of complete information.
Different extensive forms might have the same normal form.
Mixed Strategies, Beliefs, and Expected Payoffs
(Watson, Chapter 4)
Mixed Strategy
- Play one element of your strategy space
with probability 1, others with probability 0 - Example: "Play heads" or "play tails"
Pure Strategy
- Place positive probability on more than one element of your strategy space
- Example: "Flip a coin and play whatever comes up on top."
Equilibria with mixed strategies are sometimes the only equilibrium!
- Your probability distribution over another player's strategies
- Represents the probability you believe they'll play each strategy (for whatever reason)
Beliefs
- Your probability distribution over your own strategies.
- Represents the probability with which you intend to play each strategy
Mixed Strategies
A
B
X
Y
1
2
5
4
5
0
0
4
4
4
Mixed strategy for player 1:
probability distribution
over {A, B}
Belief for player 1:
probability distribution over {X, Y}
2
Expected Payoffs
\({1 \over 6}\)
\({1 \over 3}\)
\({1 \over 2}\)
\(0\)
Player 1's beliefs
\({1 \over 6} \times 6 + {1 \over 3} \times 3 + {1 \over 2} \times 2 + 0 \times 7\)
\(=3\)
Player 1's expected payoffs from each of their strategies
\(X\)
\(A\)
1
\(B\)
\(C\)
\(D\)
\(Y\)
\(Z\)
6
6
,
3
6
,
2
8
,
7
0
,
12
6
,
6
3
,
0
2
,
5
0
,
6
0
,
0
9
,
6
8
,
11
4
,
Your expected payoff from playing one of your strategies
is the weighted average of the payoffs, weighted by your beliefs about what the other person is playing
2
\({1 \over 6}\)
\({1 \over 3}\)
\({1 \over 2}\)
\(0\)
Player 1's beliefs
\(X\)
\(A\)
1
\(B\)
\(C\)
\(D\)
\(Y\)
\(Z\)
6
6
,
3
6
,
2
8
,
7
0
,
12
6
,
6
3
,
0
2
,
5
0
,
6
0
,
0
9
,
6
8
,
11
4
,
pollev.com/chrismakler
Given these beliefs, what is player 1's expected payoff from playing Y?
Expected Payoffs
2
Your expected payoff from playing one of your strategies
is the weighted average of the payoffs, weighted by your beliefs about what the other person is playing
Expected Payoffs
\({1 \over 6}\)
\({1 \over 3}\)
\({1 \over 2}\)
\(0\)
Player 1's beliefs
\({1 \over 6} \times 6 + {1 \over 3} \times 3 + {1 \over 2} \times 2 + 0 \times 7\)
\(=3\)
\({1 \over 6} \times 12 + {1 \over 3} \times 6 + {1 \over 2} \times 0 + 0 \times 5\)
\(=4\)
\({1 \over 6} \times 6 + {1 \over 3} \times 0 + {1 \over 2} \times 6 + 0 \times 11\)
\(=4\)
Player 1's expected payoffs from each of their strategies
\(X\)
\(A\)
1
\(B\)
\(C\)
\(D\)
\(Y\)
\(Z\)
6
6
,
3
6
,
2
8
,
7
0
,
12
6
,
6
3
,
0
2
,
5
0
,
6
0
,
0
9
,
6
8
,
11
4
,
\(X\)
\(A\)
1
2
\(B\)
\(C\)
\(D\)
\(Y\)
\(Z\)
6
6
,
3
6
,
2
8
,
7
0
,
12
6
,
6
3
,
0
2
,
5
0
,
6
0
,
0
9
,
6
8
,
11
4
,
If you are playing a mixed strategy, and the other player is playing a pure strategy, your expected payoff is the weighted average given the way you are mixing.
Expected Payoffs
\({1 \over 6}\)
\({1 \over 3}\)
\({1 \over 2}\)
\(0\)
Player 2's strategy
\({1 \over 6} \times 6 + {1 \over 3} \times 6 + {1 \over 2} \times 8 + 0 \times 0\)
\(=7\)
\({1 \over 6} \times 6 + {1 \over 3} \times 3 + {1 \over 2} \times 2 + 0 \times 0\)
\(=3\)
\({1 \over 6} \times 0 + {1 \over 3} \times 9 + {1 \over 2} \times 8 + 0 \times 4\)
\(=7\)
Player 2's expected payoffs given each of 1's strategies
Section Preview
Simple case: linear demand, constant MC, no fixed costs
P(Q) = 14 - Q
c(Q) = 2Q
\text{No fixed costs }\Rightarrow MC = AC = 2
Baseline Example: Monopoly
P(Q) = 14 - Q
c(Q) = 2Q
\pi(Q) = P(Q)Q - c(Q)
= (14 - Q)Q - 2Q
= 14Q - Q^2 - 2Q
\text{total revenue}
\text{total cost}
14
2
units
$/unit
P(Q) = 14 - Q
MC = AC = 2
\text{No fixed costs }\Rightarrow MC = AC = 2
14
P
Q
Baseline Example: Monopoly
P(Q) = 14 - Q
c(Q) = 2Q
\pi(Q) = P(Q)Q - c(Q)
= (14 - Q)Q - 2Q
= 14Q - Q^2 - 2Q
\text{total revenue}
\text{total cost}
14
2
units
$/unit
P(Q) = 14 - Q
MC = AC = 2
\text{No fixed costs }\Rightarrow MC = AC = 2
14
P
Q
Profit
Baseline Example: Monopoly
P(Q) = 14 - Q
c(Q) = 2Q
\pi(Q) = P(Q)Q - c(Q)
= (14 - Q)Q - 2Q
= 14Q - Q^2 - 2Q
\pi'(Q) = 14 - 2Q - 2 = 0
Q^* = 6
\text{total revenue}
\text{total cost}
\text{marginal revenue}
\text{marginal cost}
P^* = 14 - 6 = 8
\pi^* = 8\times 6 - 2 \times 6 = 36
14
8
2
6
Q
P
P(Q) = 14 - Q
MR(Q) = 14 - 2Q
MC = AC = 2
36
Next Steps
- Section: review of the monopoly model
- Tuesday: Analyzing a single player's optimal behavior in a static game; introduction to Cournot duopoly
- Thursday: Analyzing equilibrium in a static game, and in the Cournot model
Econ 51 | 07 | Introduction to Game Theory
By Chris Makler
Econ 51 | 07 | Introduction to Game Theory
Notation and definitions
