pollev.com/chrismakler

Will you need a left-handed desk for exams?
Demand Functions and Demand Curves
Christopher Makler
Stanford University Department of Economics
Econ 50: Lecture 8
where we'll be in week 7...
what we've done so far...
Friday
Monday
Wednesday
Preferences & Utility
Marginal Rate of Substitution
Utility Function Examples
Budget Constraints
Utility Maximization subject to a Budget Constraint
Cases when
Calculus Doesn't Work
Demand Functions and Demand Curves
Midterm I
Decomposing a Price Change into Income & Substitution Effects
Demand Curve Shifters: Complements & Substitutes
Unit I: Consumer Theory
Welcome
Week 1
Week 2
Week 3
Week 4
Cost Minimization
✅
✅
✅
✅
✅
✅
✅
IF...
THEN...
The consumer's preferences are "well behaved"
-- smooth, strictly convex, and strictly monotonic
\(MRS=0\) along the horizontal axis (\(x_2 = 0\))
The budget line is a simple straight line
The optimal consumption bundle will be characterized by two equations:
More generally: the optimal bundle may be found using the Lagrange method
\(MRS \rightarrow \infty\) along the vertical axis (\(x_1 \rightarrow 0\))
Cobb-Douglas
Quasilinear
Perfect Substitutes
TANGENCY CONDITION
Ray from origin, will always intersect budget line =>
Lagrange always works
Vertical line, may or may not intersect BL in first quadrant =>
Lagrange sometimes works
Tries to equate two constants, which you just can't do =>
Lagrange never works
Last Class: What is the optimal bundle for a given budget line?
Today: What happens to the optimal bundle when prices/income change?
🍏
🍌
BL1
We will be solving for the optimal bundle
as a function of income and prices:
The solutions to this problem will be called the demand functions. We have to think about how the optimal bundle will change when \(p_1,p_2,m\) change.
BL2
Specific Prices & Income
General Prices & Income
Plug tangency condition back into constraint:
Tangency Condition: \(MRS = p_1/p_2\)
Specific Prices & Income
General Prices & Income
OPTIMAL BUNDLE
DEMAND FUNCTIONS
(optimization)
(comparative statics)
The Demand Function Illustrates Three Relationships
...its own price changes?
Movement along the demand curve
...the price of another good changes?
Complements
Substitutes
Independent Goods
How does the quantity demanded of a good change when...
...income changes?
Normal goods
Inferior goods
Giffen goods
(possible) shift of the demand curve
(Friday)
Three Relationships
...its own price changes?
Movement along the demand curve
How does the quantity demanded of a good change when...
The demand curve for a good
shows the quantity demanded of that good
as a function of its own price
holding all other factors constant
(ceteris paribus)
DEMAND CURVE FOR GOOD 1
"Good 1 - Good 2 Space"
"Quantity-Price Space for Good 1"
Note: Maximum Possible Quantity Demanded

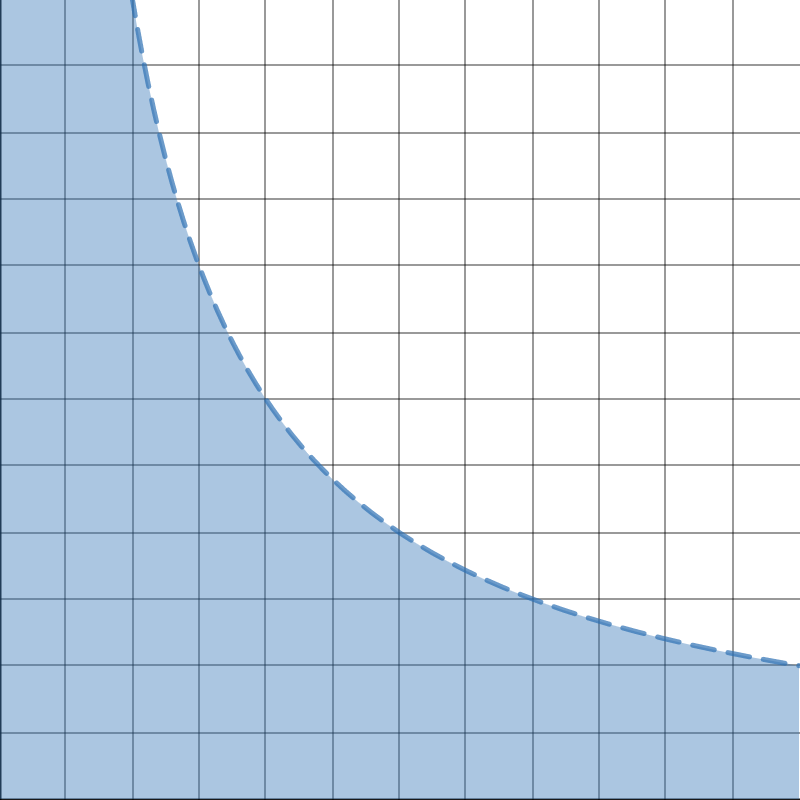

Quantity of Good 1 \((x_1)\)
Price of Good 1 \((p_1)\)
All demand curves must be in this region
Quantity bought at each price if you spent all your money on good 1
Cobb-Douglas Demand
Plug tangency condition into
the (generic) budget constraint:
Tangency Condition: \(MRS = p_1/p_2\)
Plug \(x_1^*(p_1,p_2,m)\) back
into the tangency condition:
Cobb-Douglas Demand
DEMAND FUNCTIONS
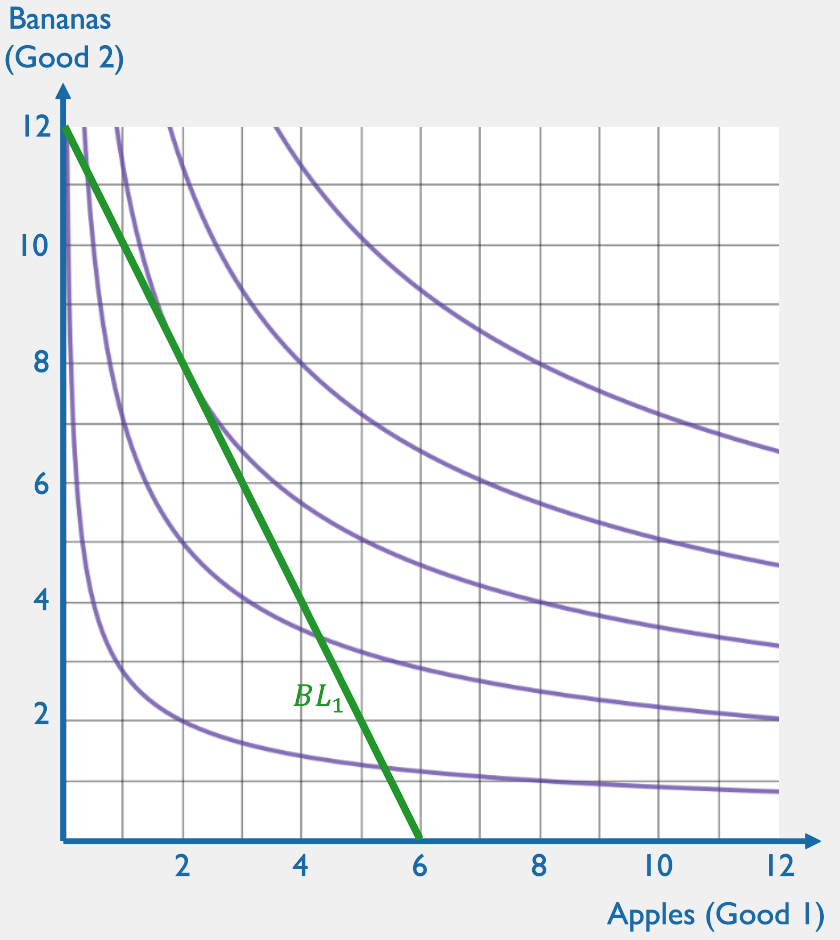
Let's think about how someone with preferences represented by this utility function would respond to a price change.
INITIAL BUDGET LINE
OPTIMAL BUNDLE
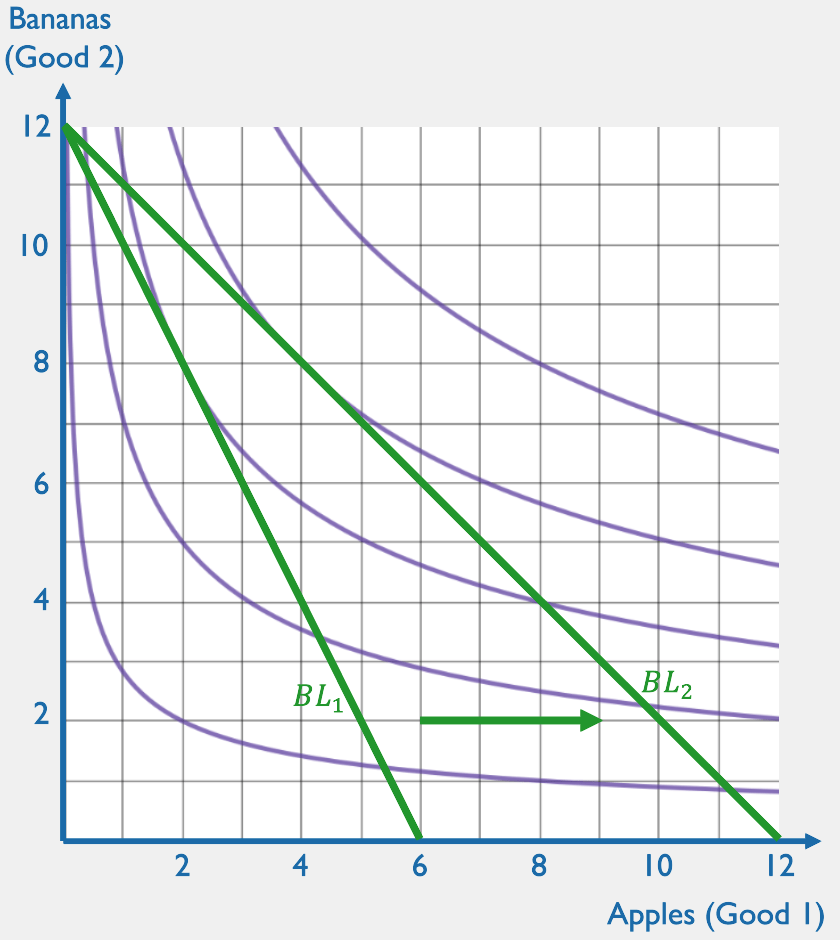
NEW BUDGET LINE
OPTIMAL BUNDLE
Cobb-Douglas Demand
DEMAND FUNCTIONS
pollev.com/chrismakler

Q. What do these demand functions mean in words?
A. "Spend \({1 \over 3}\) of your income on good 1, and \({2 \over 3}\) of your income on good 2."
For a Cobb-Douglas utility function of the form
The “Cobb-Douglas Rule"
The demand functions will be
That is, the consumer will spend fraction \(a/(a+b)\) of their income on good 1, and fraction \(b/(a+b)\) of their income on good 2.
This shortcut is very much worth memorizing! We'll use it a lot in the next few weeks in place of going through the whole optimization process.
Cobb-Douglas Demand
DEMAND FUNCTION FOR GOOD 1
DEMAND CURVE FOR GOOD 1
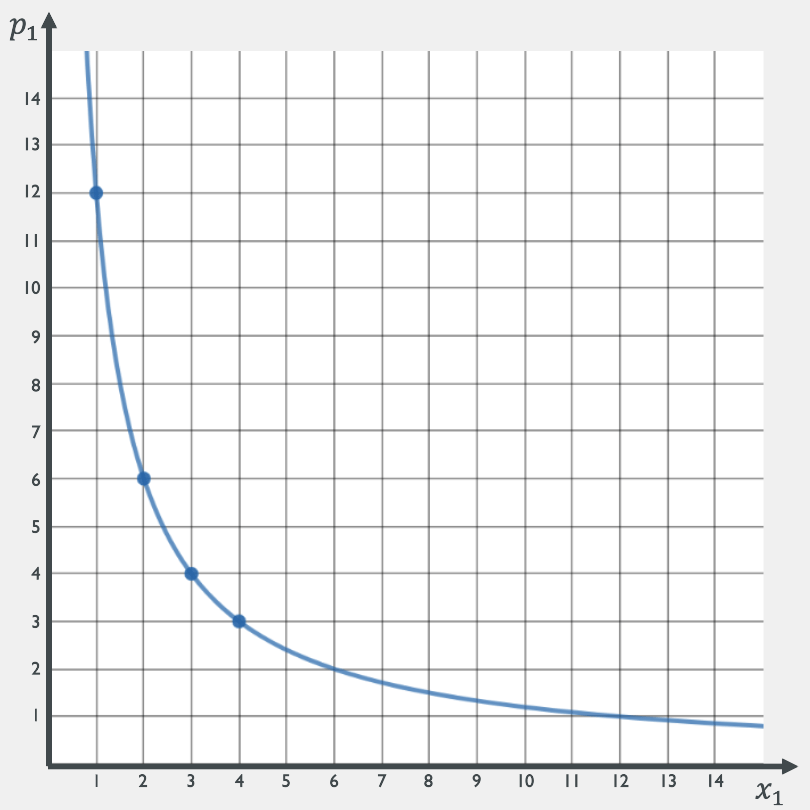
Draw the demand curve if \(p_2 = 6\), \(m = 36\)
3
4
6
12
4
3
2
1
Cobb-Douglas Demand
DEMAND FUNCTION FOR GOOD 1

DEMAND CURVE FOR GOOD 1
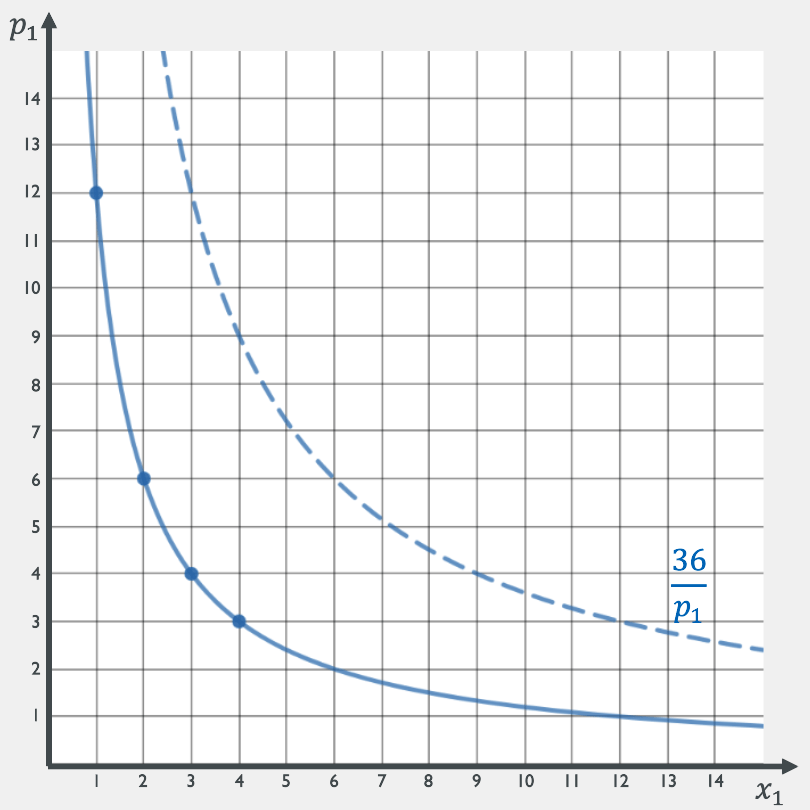
Draw the demand curve if \(p_2 = 6\), \(m = 36\)
3
4
6
12
4
3
2
1

What happens if \(m\) increases to 72?
Cobb-Douglas Demand
DEMAND FUNCTION FOR GOOD 1

DEMAND CURVE FOR GOOD 1
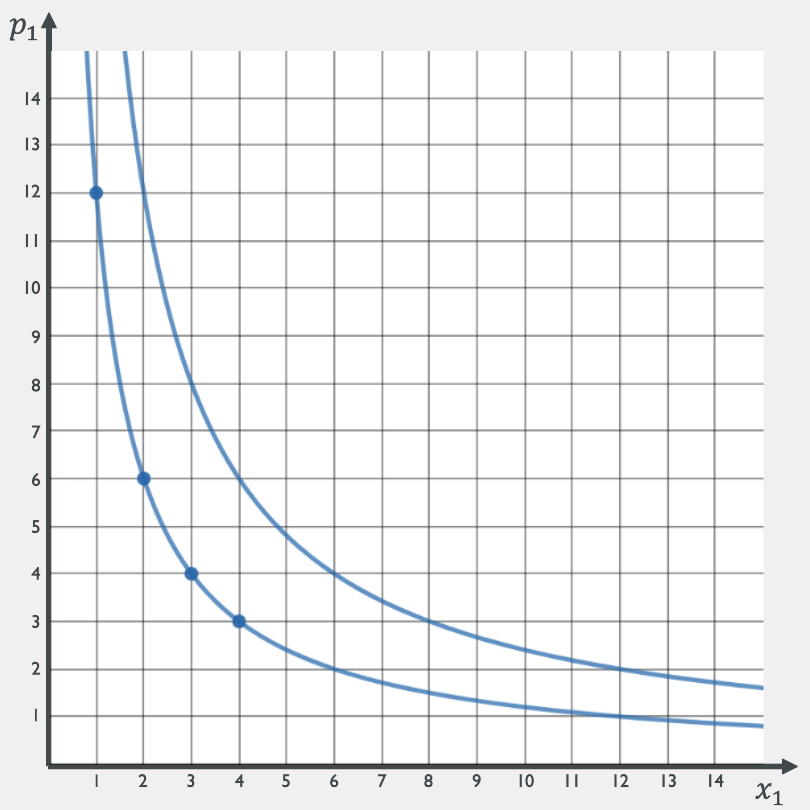
Draw the demand curve if \(p_2 = 6\), \(m = 36\)
3
4
6
12
4
3
2
1

What happens if \(m\) increases to 72?
8
6
4
2
Cobb-Douglas Demand Three Ways
MATH
"Spend \({1 \over 3}\) of your income on good 1, regardless of prices and income."
GRAPHS
WORDS


Perfect Substitutes
When is the MRS greater than the price ratio? What would you buy in that case?
ONLY BUY GOOD 1
When is the MRS less than the price ratio? What would you buy in that case?
ONLY BUY GOOD 2
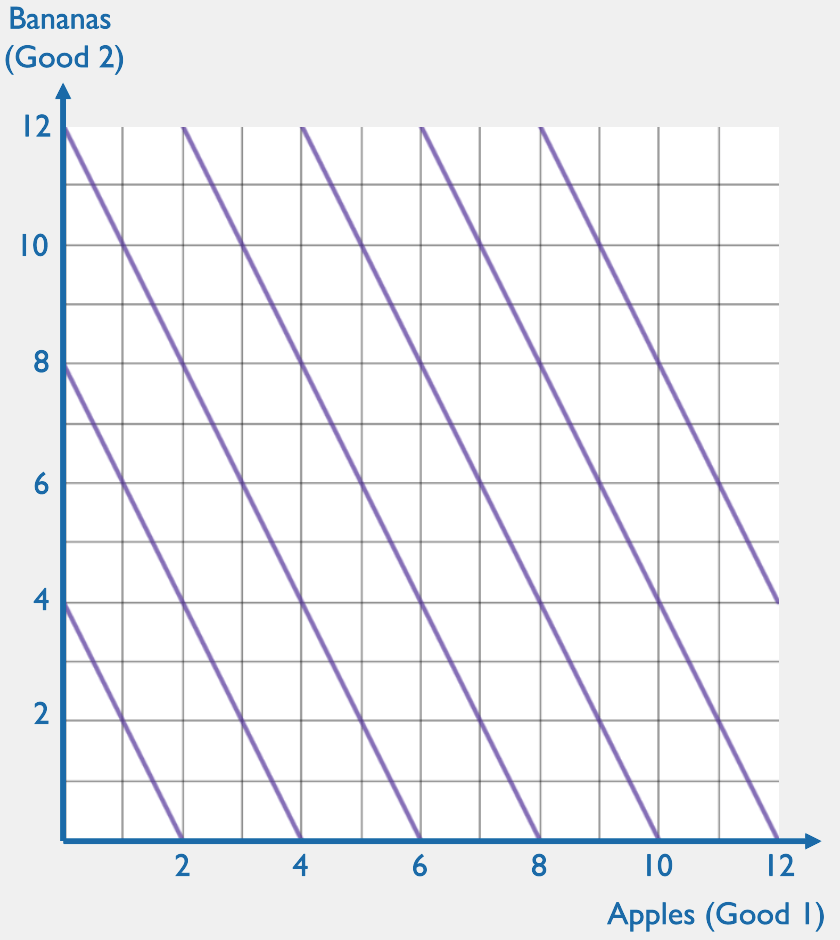
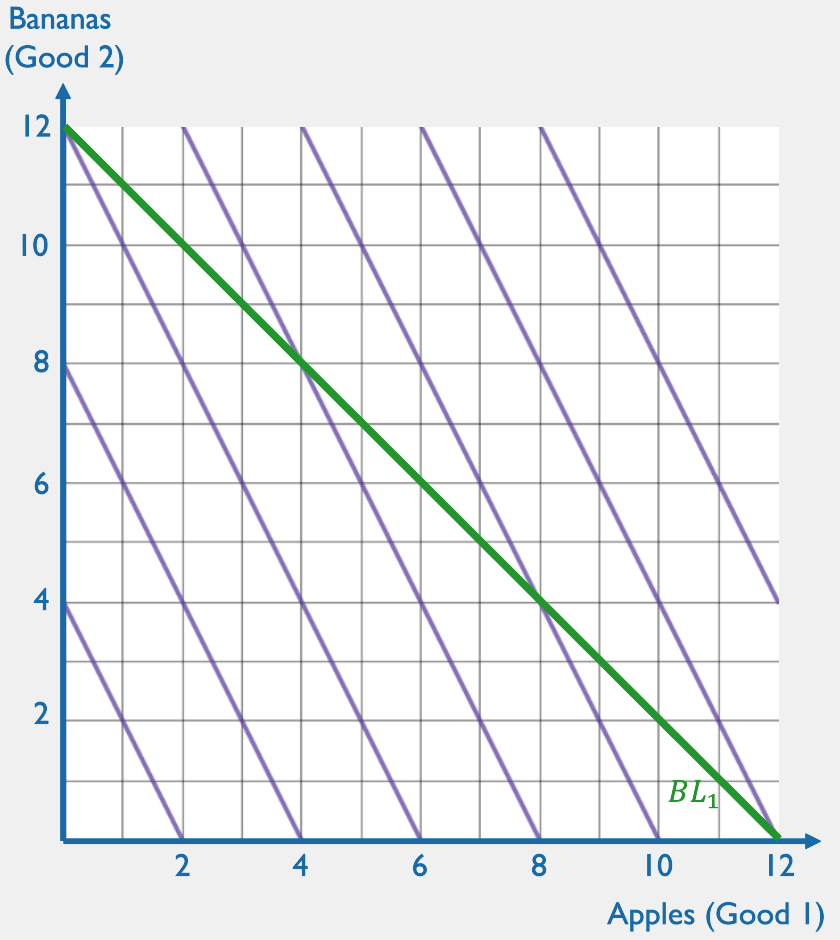
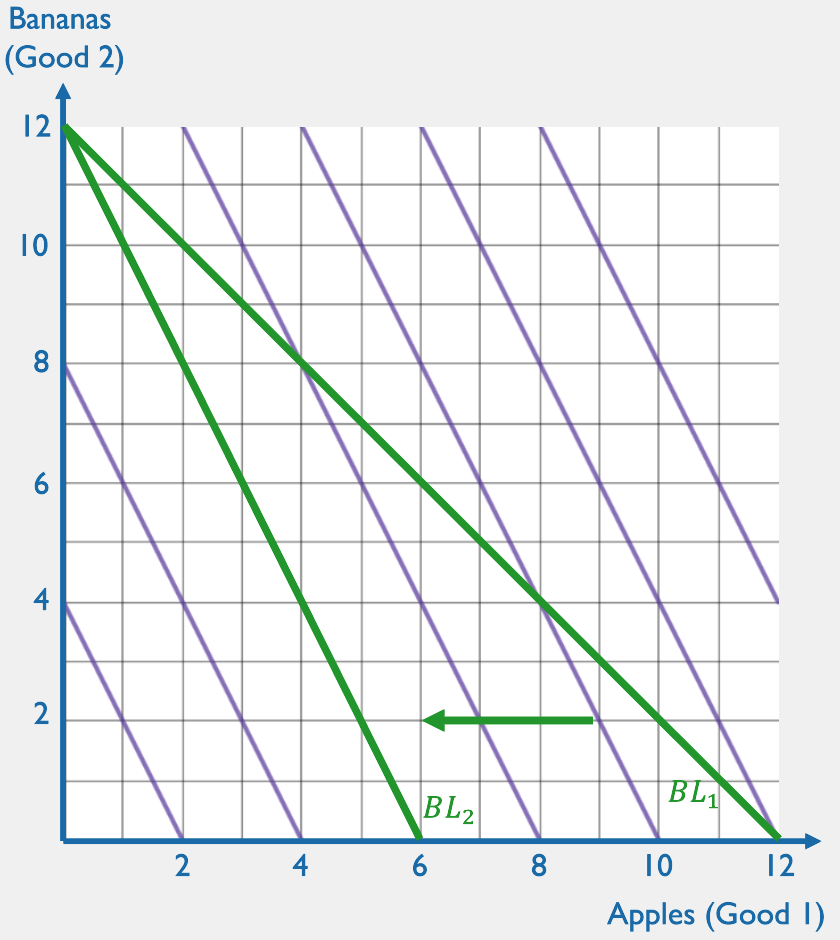
When is the MRS equal to the price ratio? What would you buy in that case?
BUY ANYTHING!
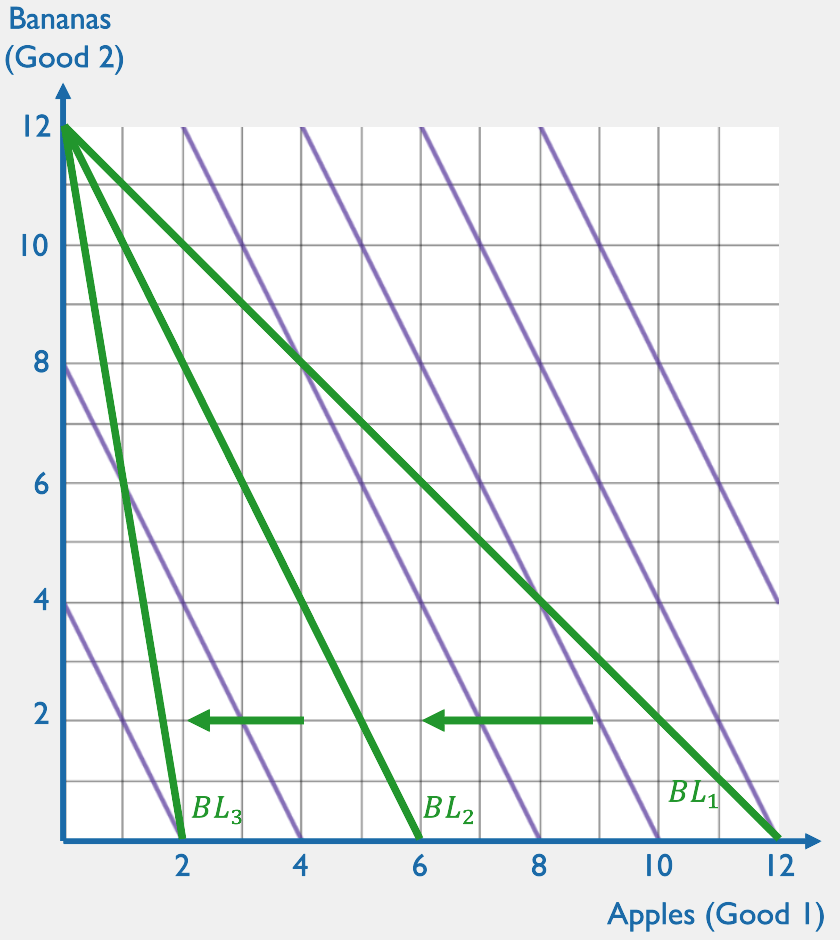
Perfect Substitutes
ONLY BUY GOOD 1
ONLY BUY GOOD 2
BUY ANYTHING!
Consumer behavior:
Intuitive description of the behavior:
If you like apples twice as much as bananas,
you'll only buy apples as long as they cost less than twice as much as bananas do!
Perfect Substitutes: General Case
ONLY BUY GOOD 1
ONLY BUY GOOD 2
BUY ANYTHING!
Consumer behavior:
How do we write this down as demand functions?
Demand for Perfect Substitutes Three Ways
MATH
GRAPHS
WORDS
"Always buy whichever good gives you the higher bang for your buck"

Quasilinear
Plug tangency condition into
the (generic) budget constraint:
Tangency Condition: \(MU_1 = p_1\)
Suppose good 2 is "dollars spent on other goods," so \(p_2 = 1\).
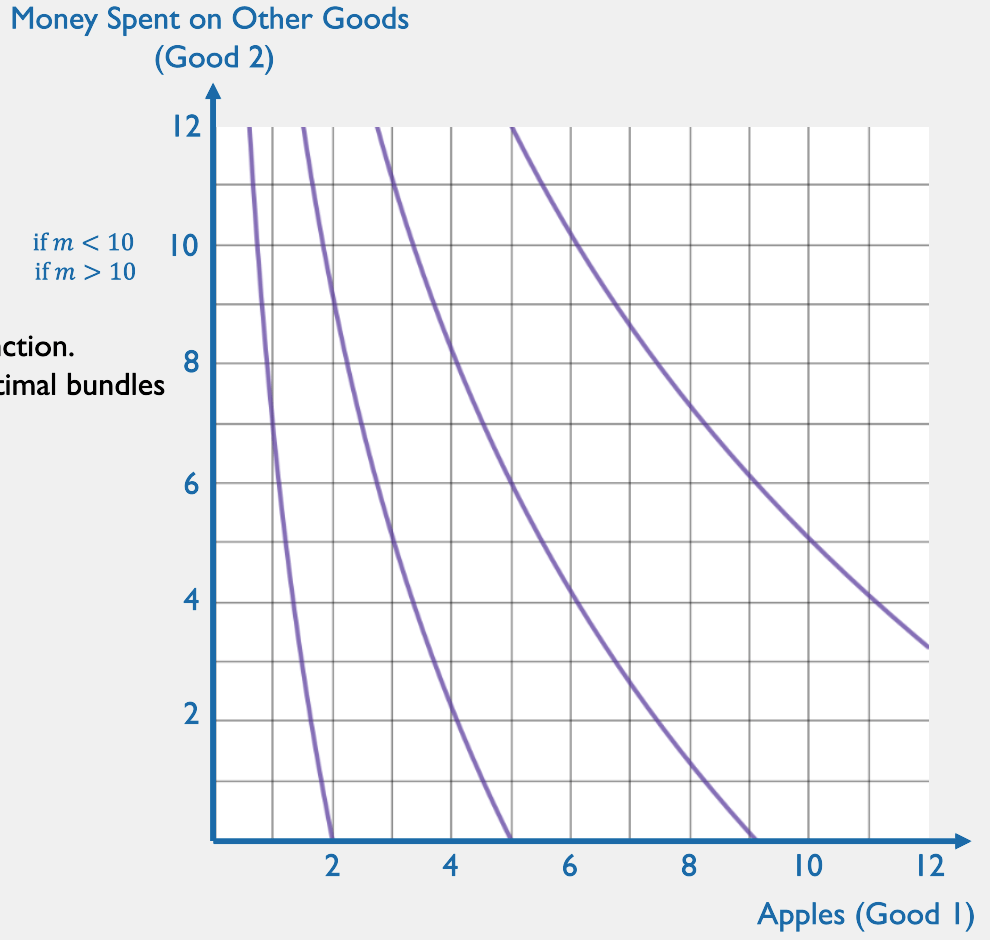
Quasilinear
Suppose good 2 is "dollars spent on other goods," so \(p_2 = 1\).

Lagrange solutions:
Are these our demand functions?
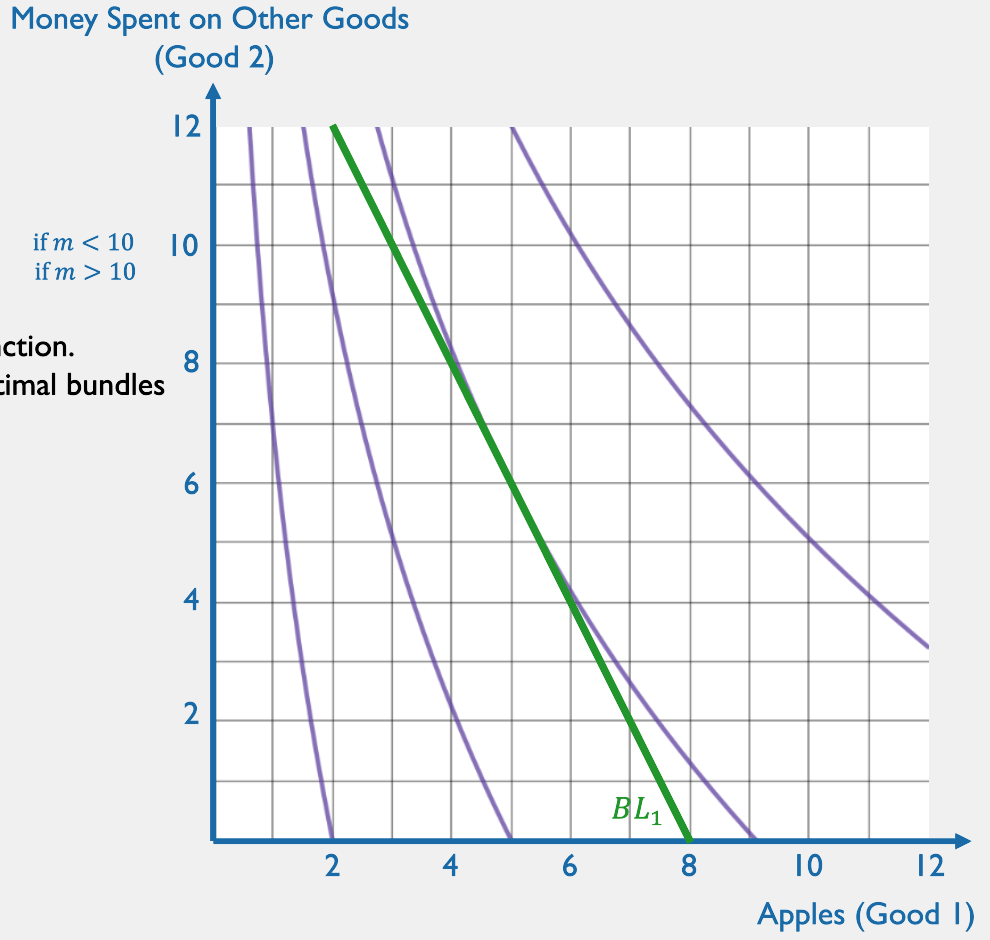
BUDGET LINE
OPTIMAL BUNDLE
LAGRANGE SOLUTION
Quasilinear
Suppose good 2 is "dollars spent on other goods," so \(p_2 = 1\).
Lagrange solutions:
Are these our demand functions?

BUDGET LINE
OPTIMAL BUNDLE
LAGRANGE SOLUTION
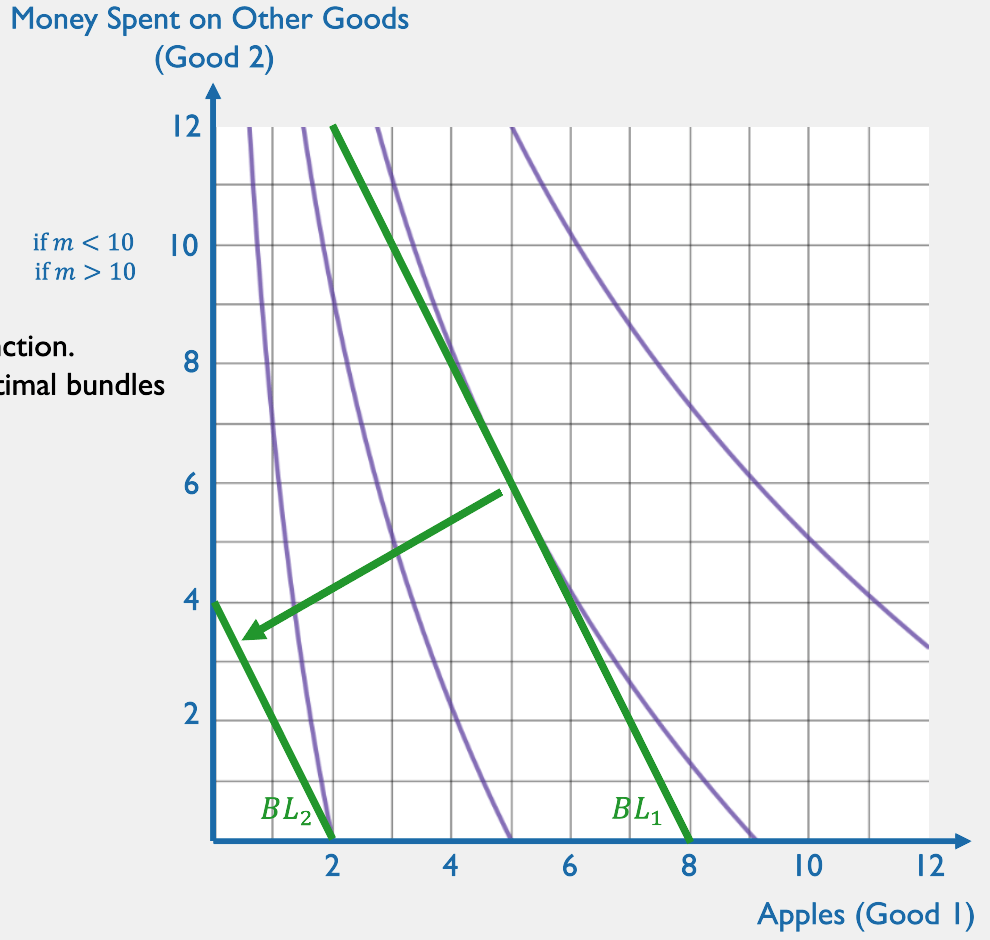
Quasilinear
Suppose good 2 is "dollars spent on other goods," so \(p_2 = 1\).
Lagrange solutions:
Consumer behavior:
"If you have at least $10, spend $10 on apples. Otherwise, spend all your money on apples."
How do we write this down as demand functions?
Demand with Quasilinear Preferences Three Ways
MATH
GRAPHS
WORDS
"Buy up to the point where your MRS equal the price ratio, if you can afford it, regardless of your income."


This can feel like you're drinking from a fire hose.
You're not alone.
What we did today
- No new mathematical techniques!
- Solved for the optimal choice as a function of prices and income
- Plotted the demand curve for a good, holding the price of other goods and income constant.
- Section: some more drawing demand functions, plus looking over some old exam questions from HW
Econ 50 | Spring 25 | Lecture 8
By Chris Makler
Econ 50 | Spring 25 | Lecture 8
Demand Functions and Demand Curves
- 832



