
Tópico 5
Fundamentos da Mecânica
Prof. Ronai Lisbôa
BCT - ECT - UFRN
O que é o movimento? Por que estudamos esse conceito?
Unificando conceitos
Os conteúdos
Aplicações
| Relações: - Deslocamento, Distância - Velocidade, Rapidez - Vetores, escalares. |
|---|
| Entendendo os padrões e escalas do movimento |
|---|
| Sistemas e modelos - Sistema de coordenada global - Movimento é relativo ao nosso sistema de coordenadas - Sistema de posicionamento global. |
|---|
| As leis físicas são observadas ao nosso redor. |
|---|
| Medidas de latitude e longitude |
|---|
| Medidas de velocidade e rapidez |
|---|
| Algarismos significativos |
|---|
| Taxas de variação |
|---|
| Escalares e vetores |
|---|
| Gráficos e análise de dados |
|---|
| Medindo deslocamento e distância |
|---|
| Compreendendo o sistemas de coordenadas global |
|---|
| Determinação das melhores linhas de ajuste e determinação de inclinações a partir de gráficos |
|---|
| Sistemas testes |
|---|
| Cálculos com planilhas |
|---|
| Sistemas testes |
|---|
| Caminhando, correndo, dirigindo |
|---|
| Sistema solar |
|---|
| Deriva continental |
|---|
| Comunicações |
|---|
| Navegação |
|---|
| Telemetria da vida selvagem |
|---|
| Acompanhamento do movimento das pessoas |
|---|
Fonte: Lawrence Berkeley LaboratoryFONTE DA ATIVIDADE
Movimento
Tudo no universo está em constante movimento.
Quão rápido a Terra está se movendo ao redor do Sol?
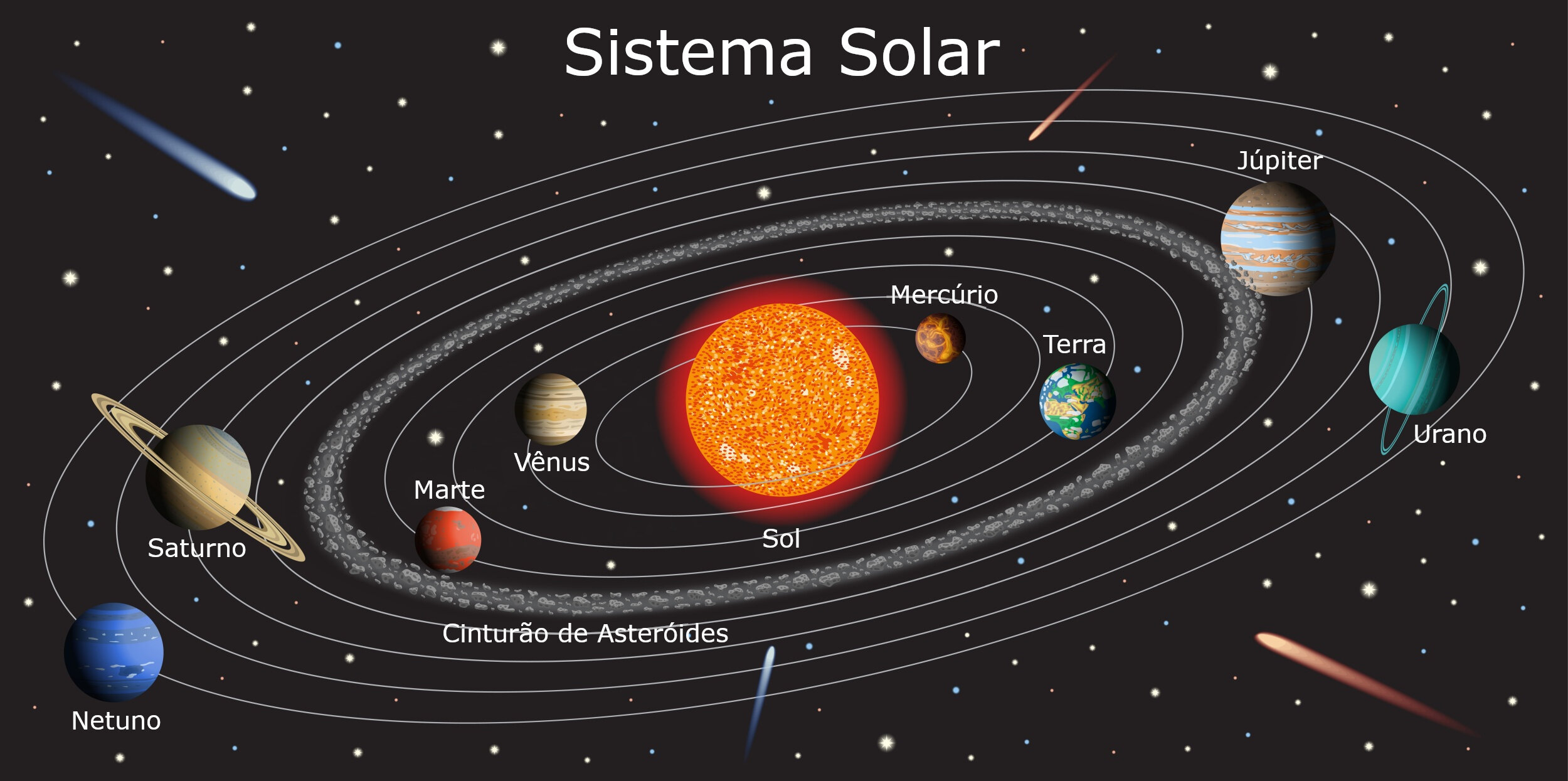
Movimento
Tudo no universo está em constante movimento.
Quão rápido o caracol está se movendo?



Movimento
Tudo no universo está em constante movimento.
Continentes “derivam” a velocidades muito lentas (2,5 cm/ano), mas podem mover-se longas distâncias ao longo de milhões de anos.
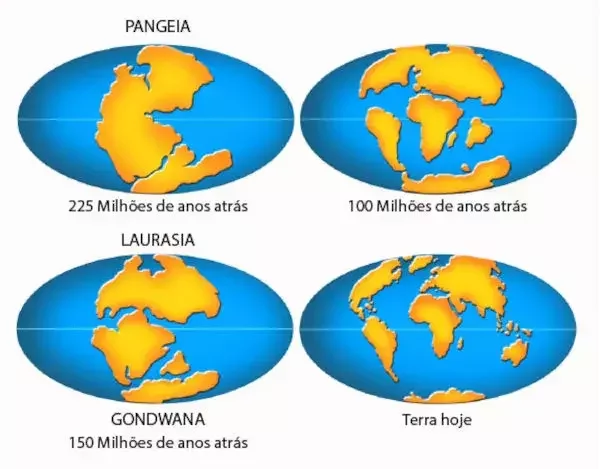
Movimento
Tudo no universo está em constante movimento.
Os sistemas de tempestades geralmente se movem lentamente, mas a velocidade do vento dentro de um furacão ou tornado pode resultar em devastação significativa.
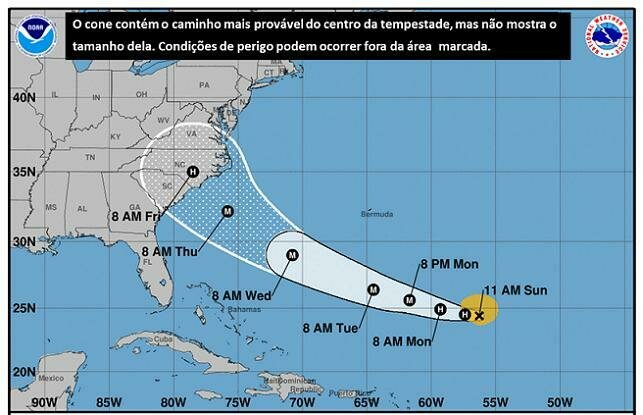
Movimento
Tudo no universo está em constante movimento.
A luz pode viajar distâncias extremamente longas a alta velocidade.
Fonte: https://exame.com
Movimento
Tudo no universo está em constante movimento.
O sinal das ondas eletromagnéticas viajam próximas à velocidade da luz em circuitos elétricos.
Fonte: https://olhardigital.com.br
Blackwell, custará entre US$ 30 mil e 40 mil por unidade

Mas a velocidade de deriva dos elétrons em um circuito é aproximadamente a velocidade de um caracol.
Fonte: https://es.linkedin.comMovimento
Tudo no universo está em constante movimento.
A velocidade média dos átomos de hélio a 25° é 1255 m/s
Blackwell, custará entre US$ 30 mil e 40 mil por unidade

Movimento
Tudo no universo está em constante movimento.
Bactérias Salmonella se movem lentamente em curtas distâncias. Proteínas, também!
Blackwell, custará entre US$ 30 mil e 40 mil por unidade
Movimento
Tudo no universo está em constante movimento.
A vida depende do movimento em uma ampla gama de escalas
Blackwell, custará entre US$ 30 mil e 40 mil por unidade
Fonte: https://coenfeba.com/
Movimento
Tudo no universo está em constante movimento.
O controle de movimento é um grande negócio.



Fonte: https://www.estadao.com.brMovimento
Tudo no universo está em constante movimento.
O movimento é um que permite as pessoas se mudarem de um lugar para outro.


Fonte: Pedro Vitorino/Cedida
Fonte: https://passeiospipa.com.brMovimento
Hoje podemos usar o Sistema de Posicionamento Global (GPS) para medir nossa localização e nos guiar para novos locais.
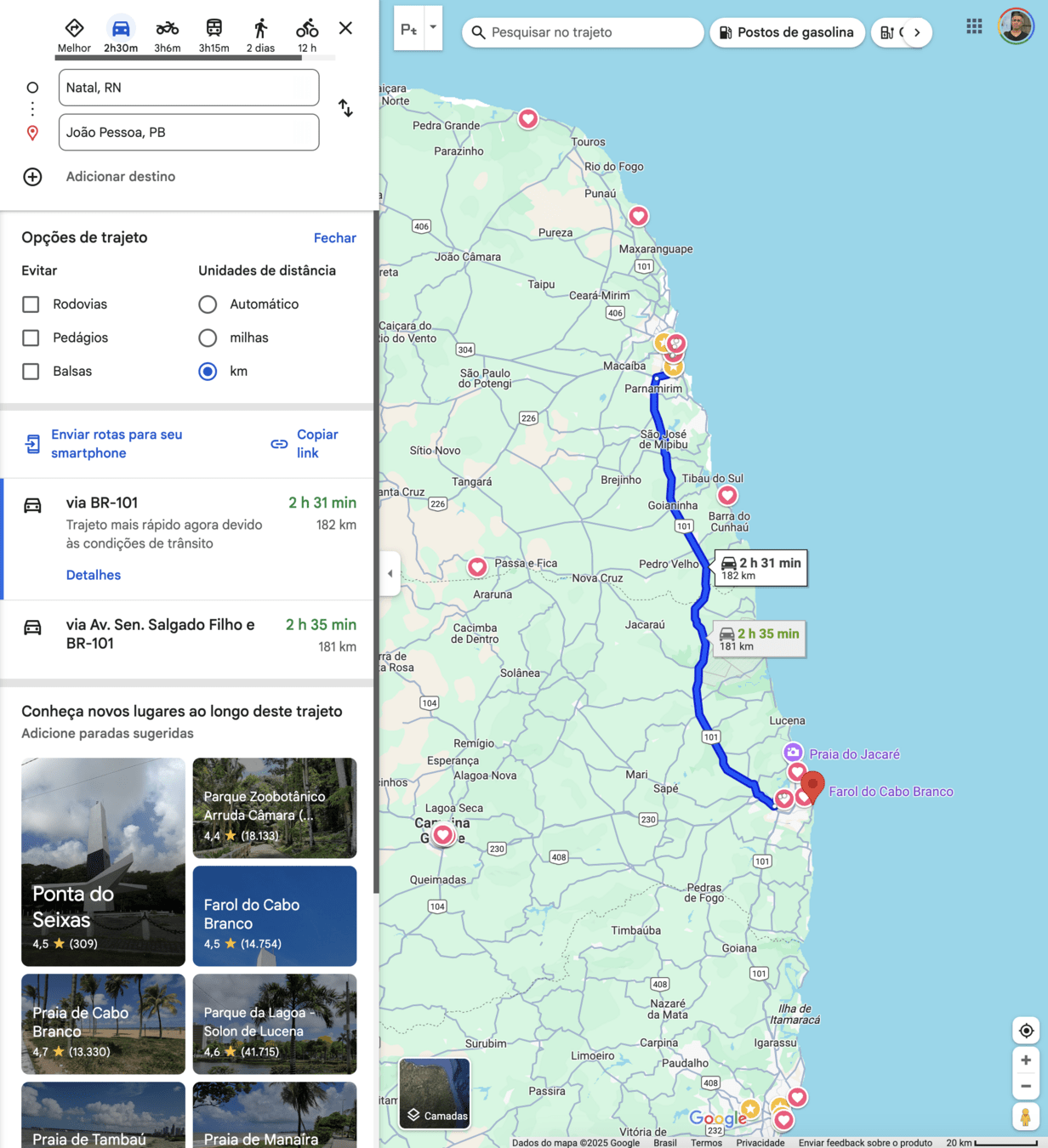
Fonte: Google Maps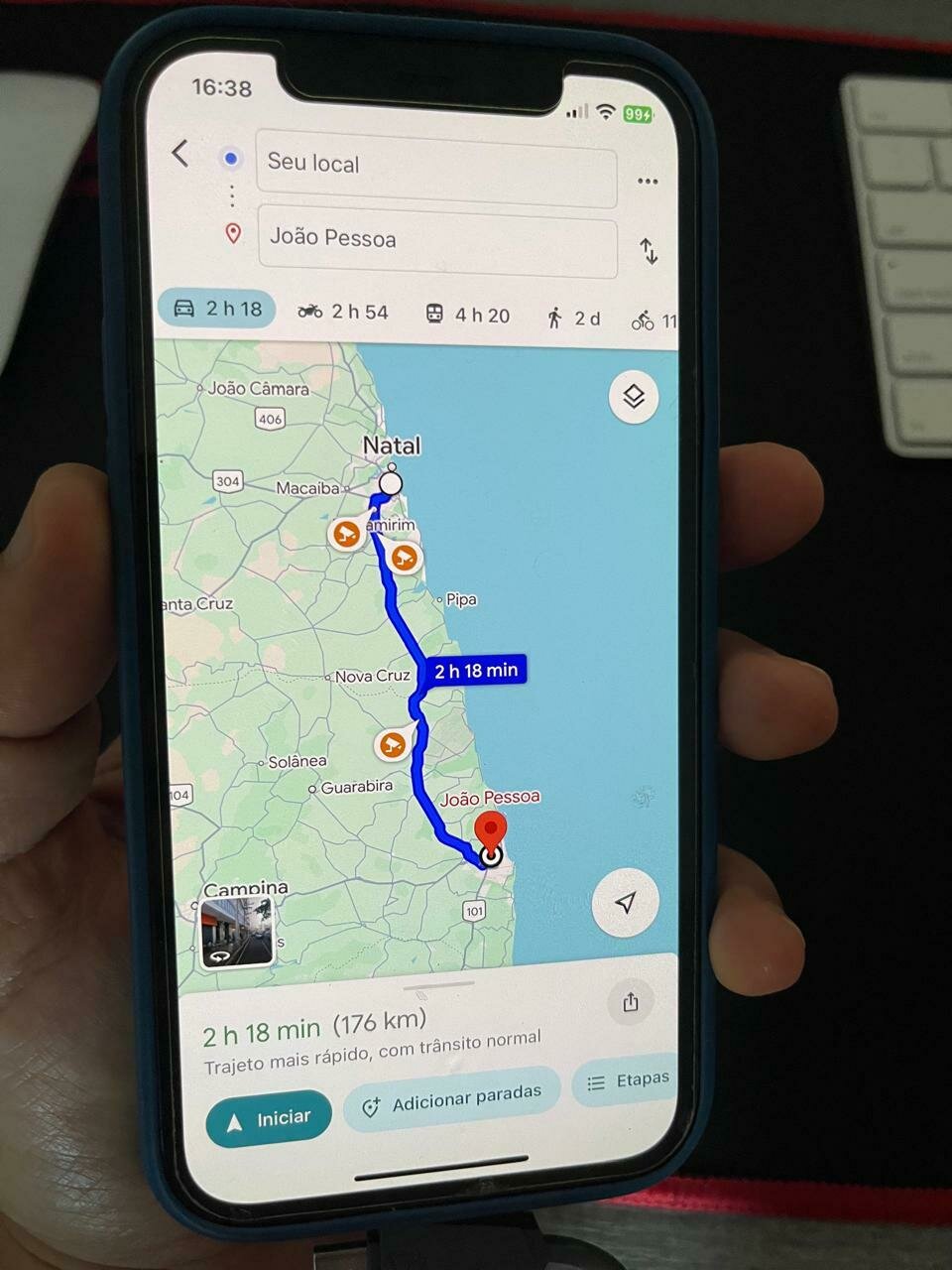
Exploraremos o movimento examinando o deslocamento e a velocidade de pessoas/objetos enquanto viajam curtas distâncias pela superfície da Terra.
Movimento
O sistema de Geoposicionamento completo inclui 24 satélites que ficam orbitando a Terra.
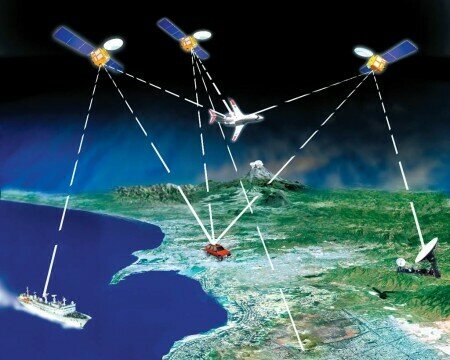
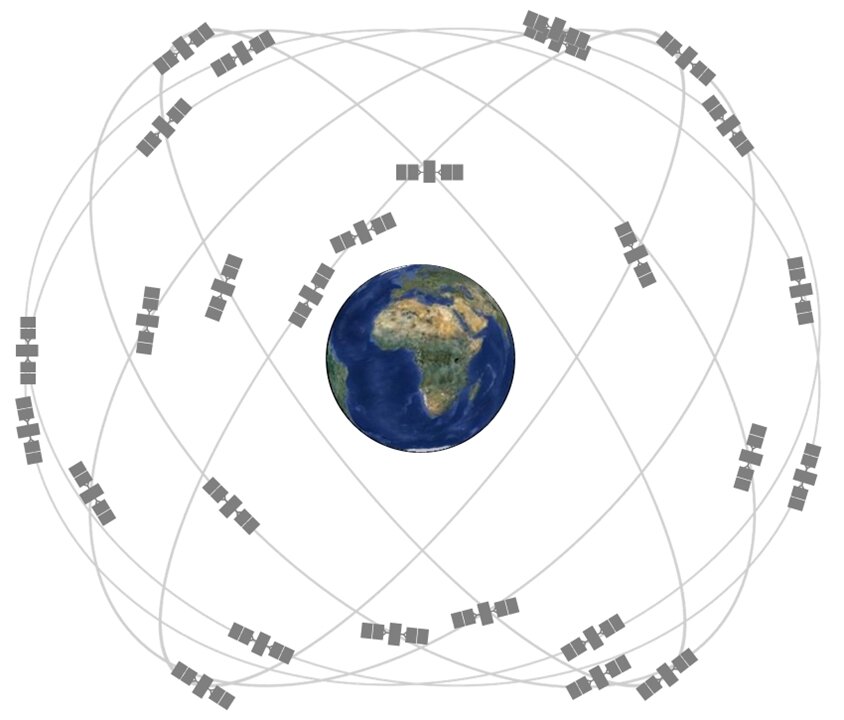
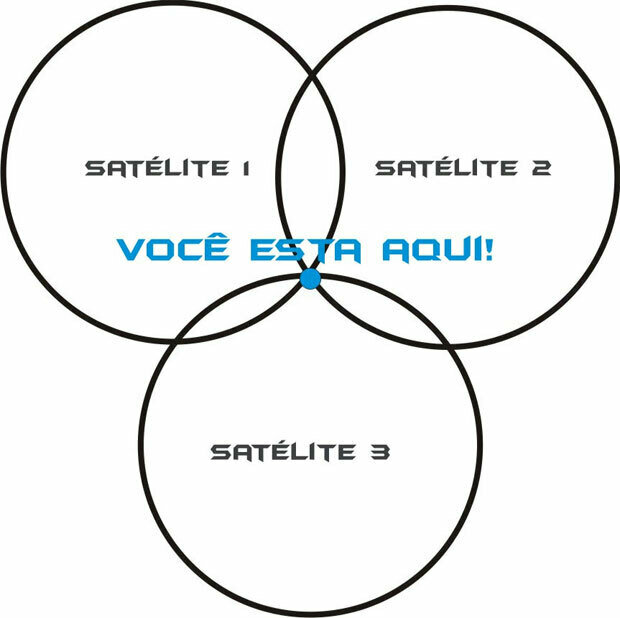
Quando você liga o seu receptor GPS e pede para ele te dizer onde você está, na verdade, você está entrando em contato com 4 desses satélites e pedindo informação.
Ao cruzar esses círculos, o ponto onde os três se cruzam é exatamente onde você está.
Movimento
Antes de passarmos a usar o GPS, vamos tirar um momento para apreciar um pouco da física envolvida na criação deste sistema.
Fonte: INPE




Sistema de Coordenadas Geográficas
Linhas imaginárias de latitude e longitude definem um sistema de coordenadas por meio do qual a posição ou localização de qualquer lugar na superfície da Terra pode ser determinada.
Fonte: GOOGLE
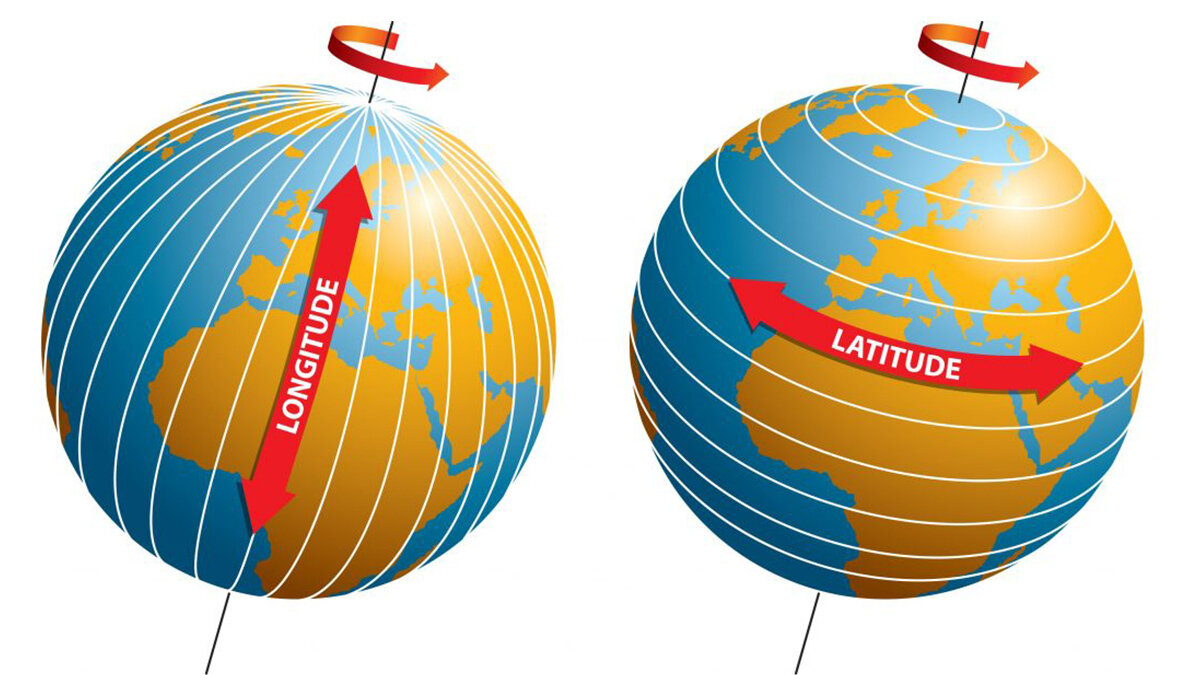
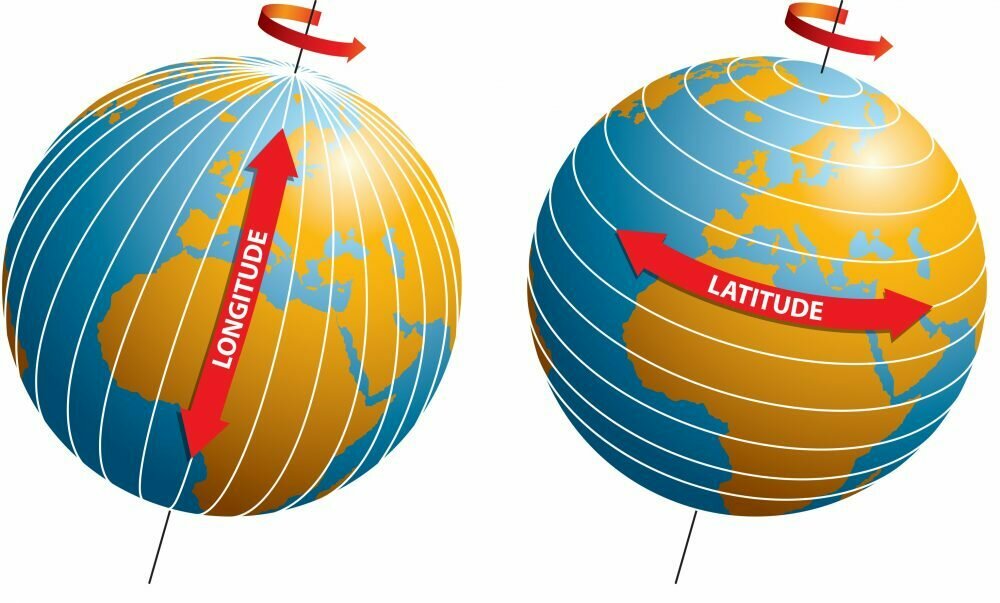
Latitude e Longitude
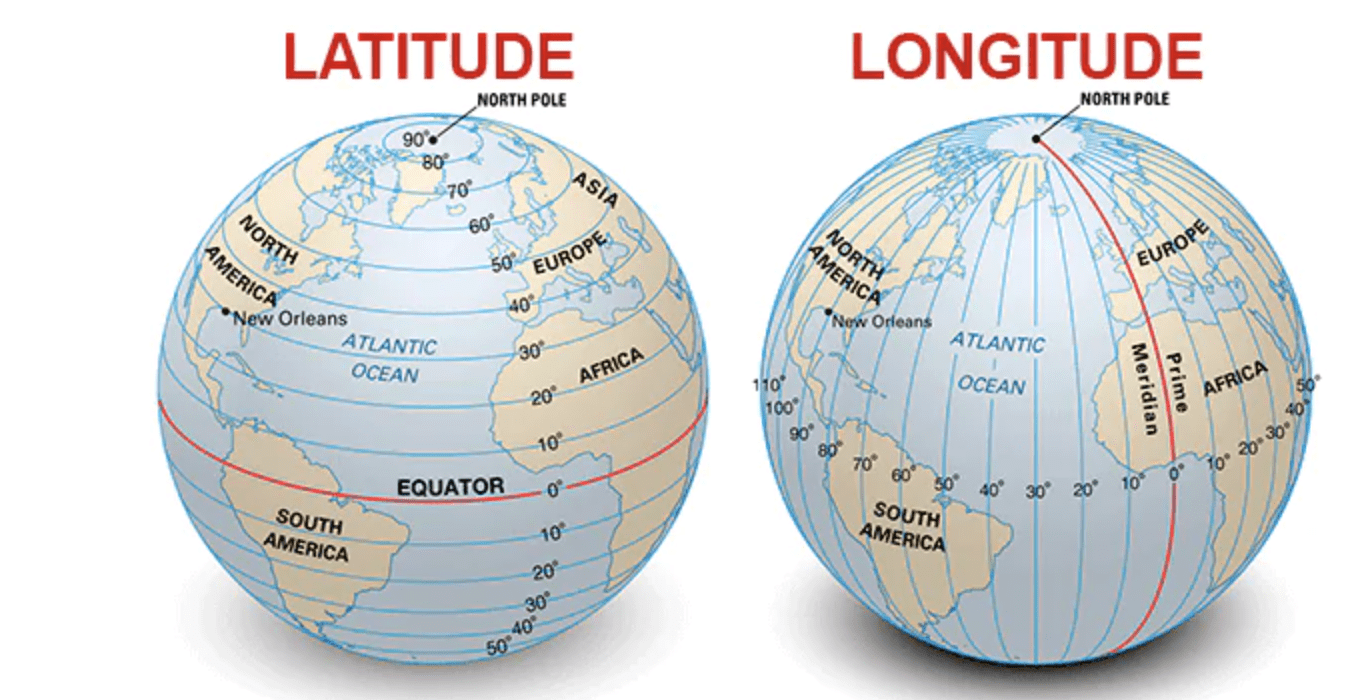
Latitude e longitude nada mais são do que nomes que as coordenadas geográficas únicas obtidas para cada ponto da superfície terrestre.
A latitude é o ângulo formado entre o ponto de interesse e o equador terrestre. A mesma é medida ao longo do meridiano que passa pelo lugar de interesse.
A longitude geográfica é o ângulo formado entre o meridiano de Greenwich e o meridiano que passa pelo ponto considerado.
Sistema de Coordenadas Geográficas
A latitude e longitude são medidas em graus (°), minutos (′) e segundos (″) ou em uma base decimal.
Fonte: Shutterstock.com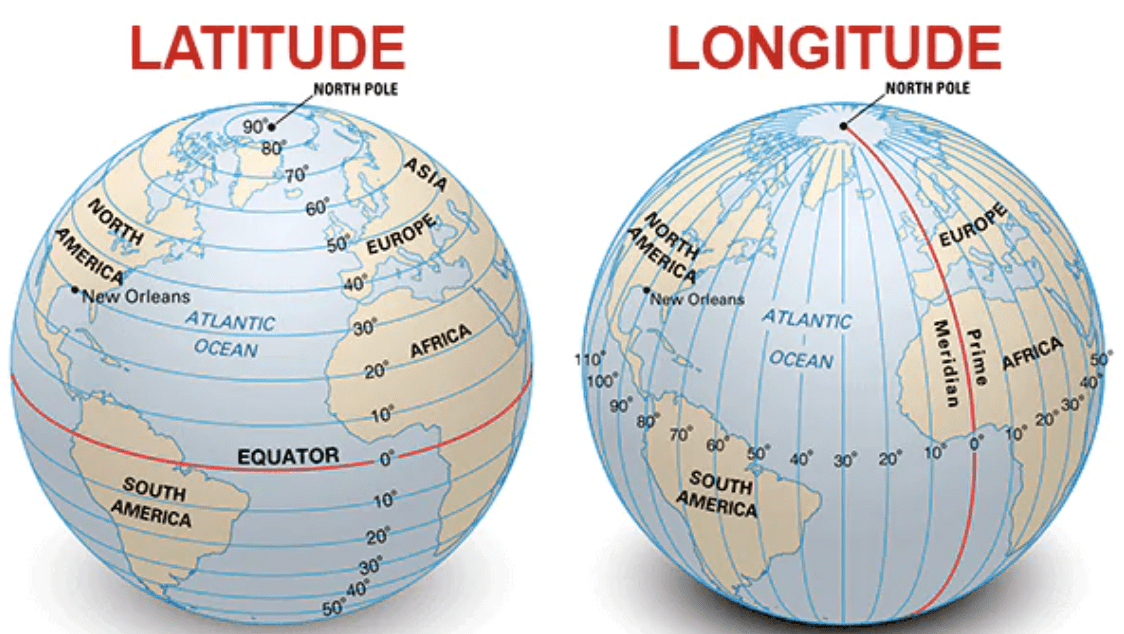
A latitude varia de 0° no Equador a 90° nos polos (Norte e Sul) . A Longitude varia de 0° no Meridiano de Greenwich a 180° a leste ou oeste.
ECT - Anel Viário Contorno do Campus s/n - Capim Macio, Natal - RN, 59078-970
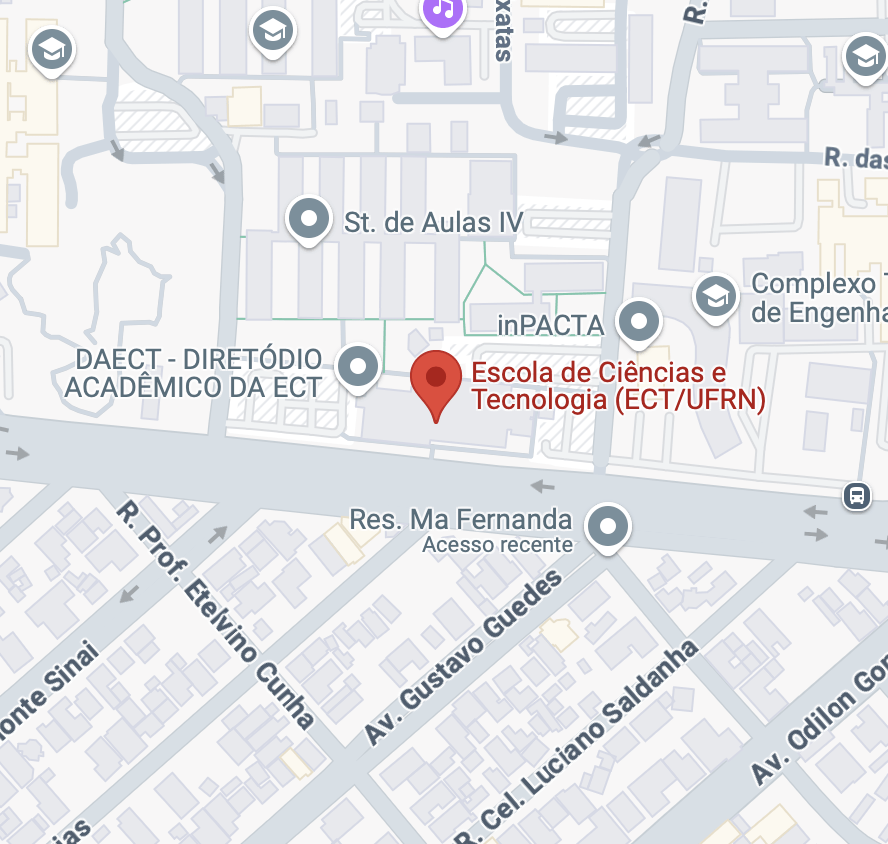
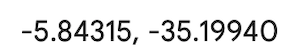
Latitude
Longitude
Fonte: Google Maps, variando de 0° no Equador a 90° nos polos (Norte e Sul).
Veja como usar o Google Maps para obter as coordenadas, aqui.
Sistema de Coordenadas Geográficas
Identifique a latitude e longitude dos pontos destacados em vermelho.
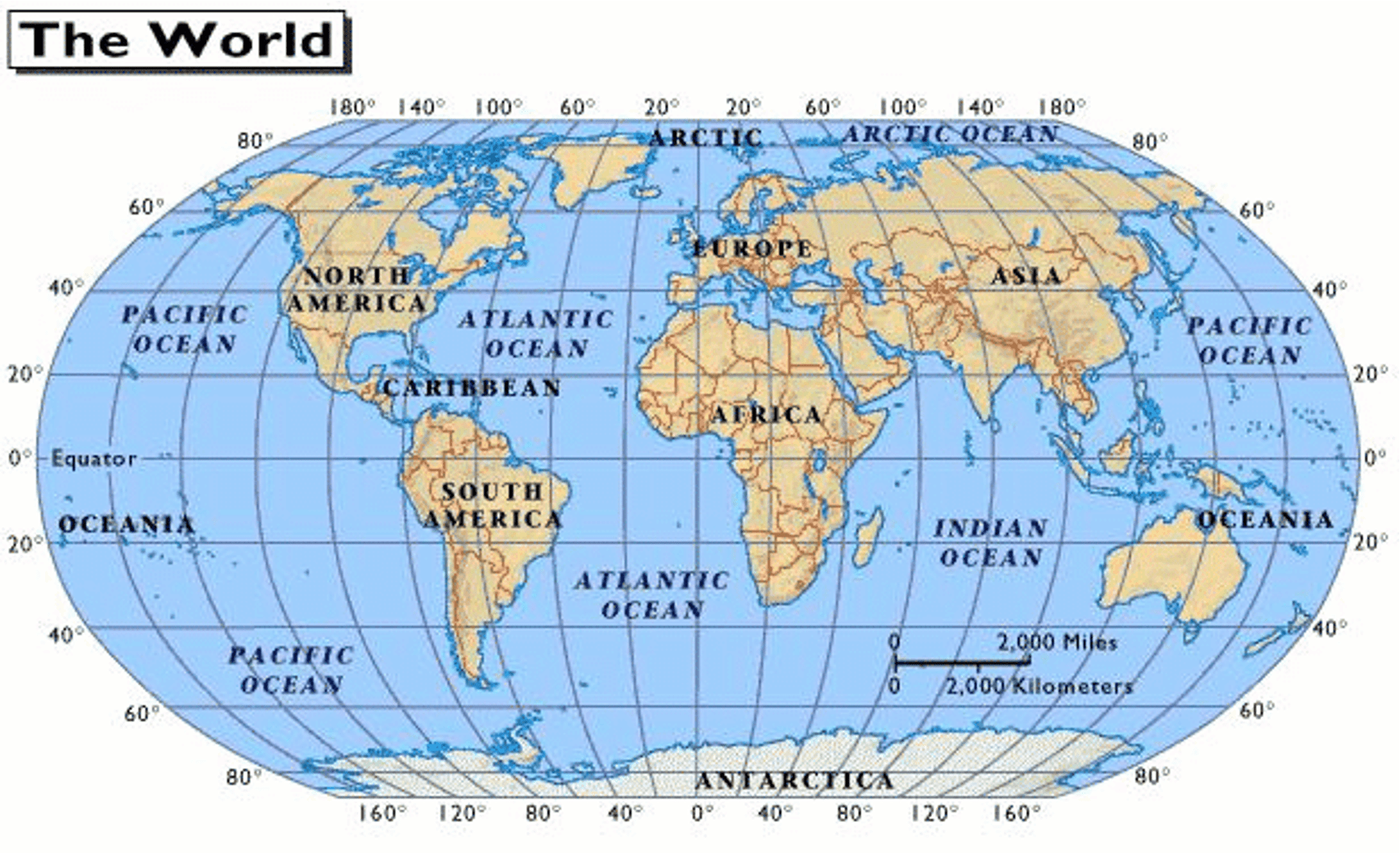
Norte
Sul
Leste
Oeste
Latitude e Longitude
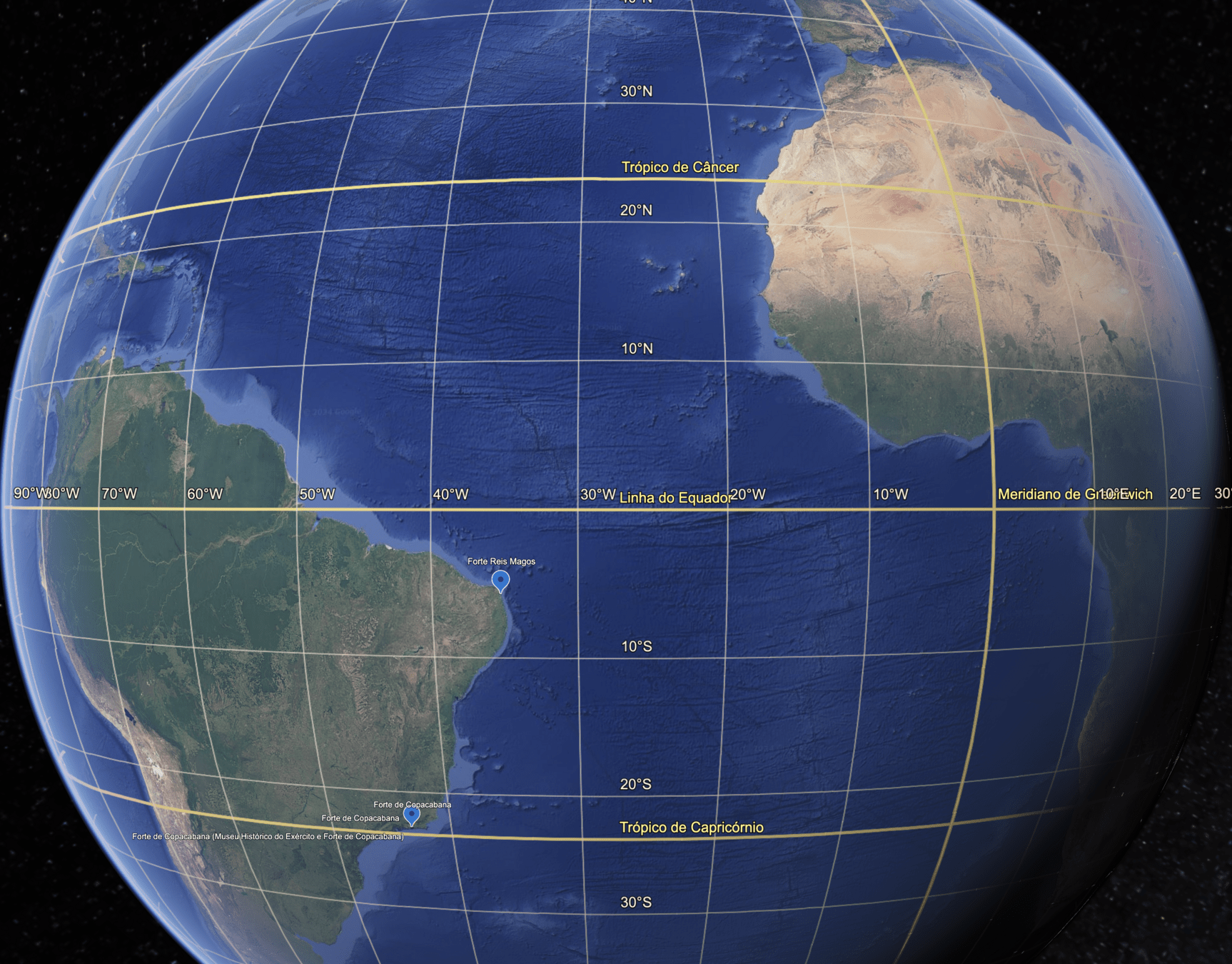
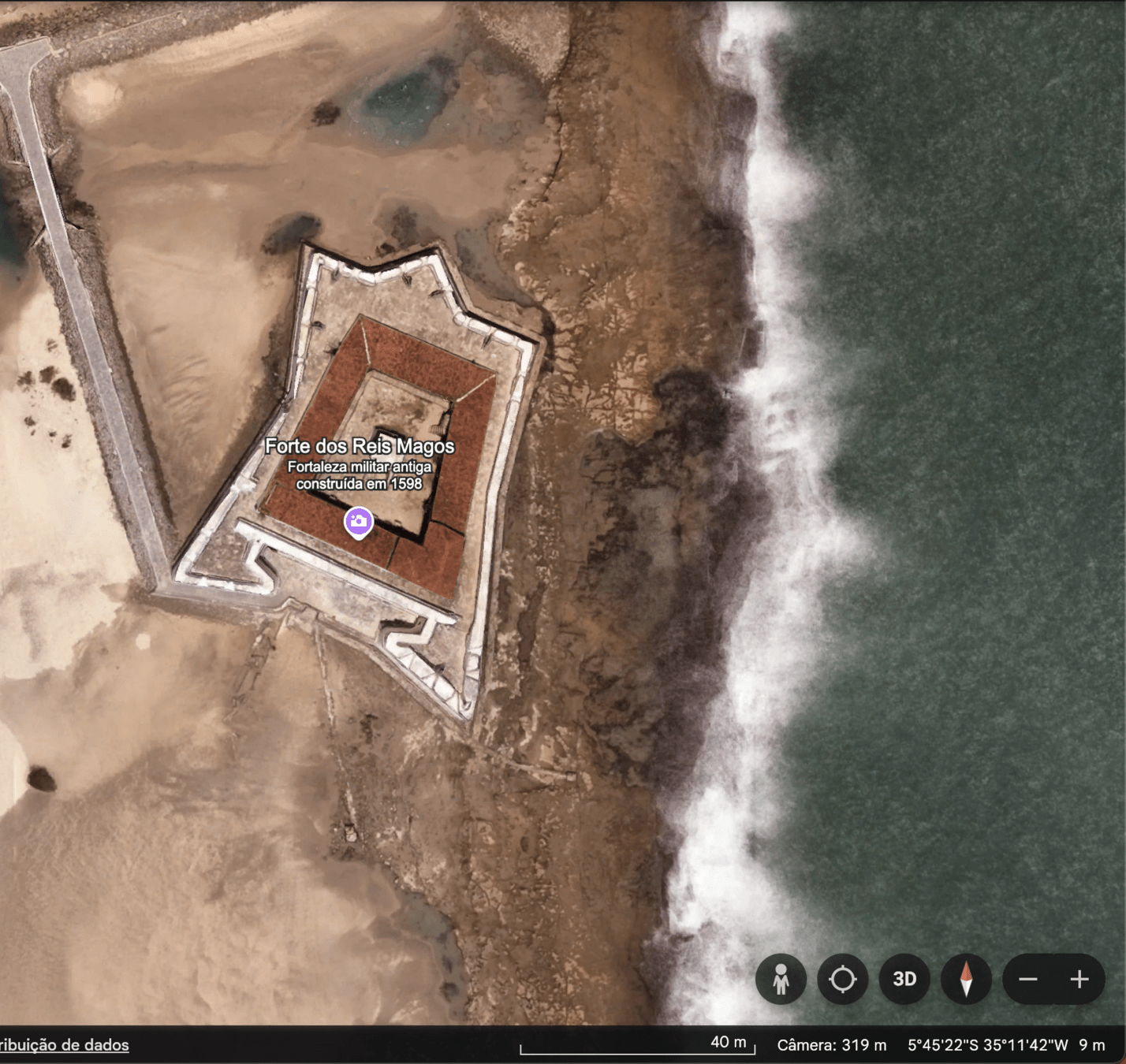

Fonte: Google EarthDMS
DMS
Que lugar é este?
Que lugar é este?
E na base decimal?
E na base decimal?
Latitude e Longitude
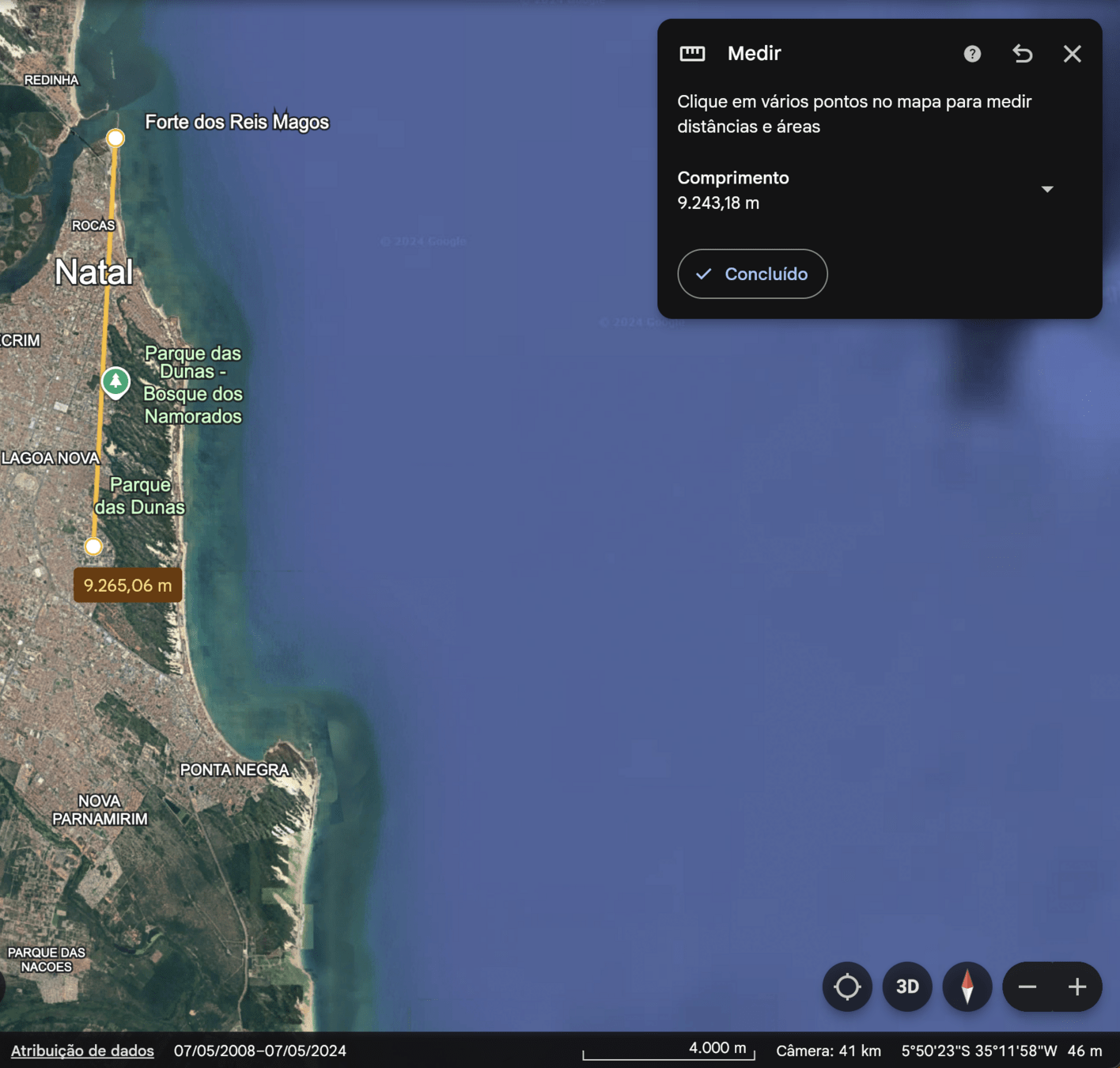
Início: Forte Reis Magos
Fim: Biblioteca Central UFRN
Distância:
A latitude mudou.
A longitude não mudou.
Latitude e Longitude
Início: Forte Reis Magos
Fim: Rio Santana
Distância:
A latitude não mudou.

A longitude mudou.
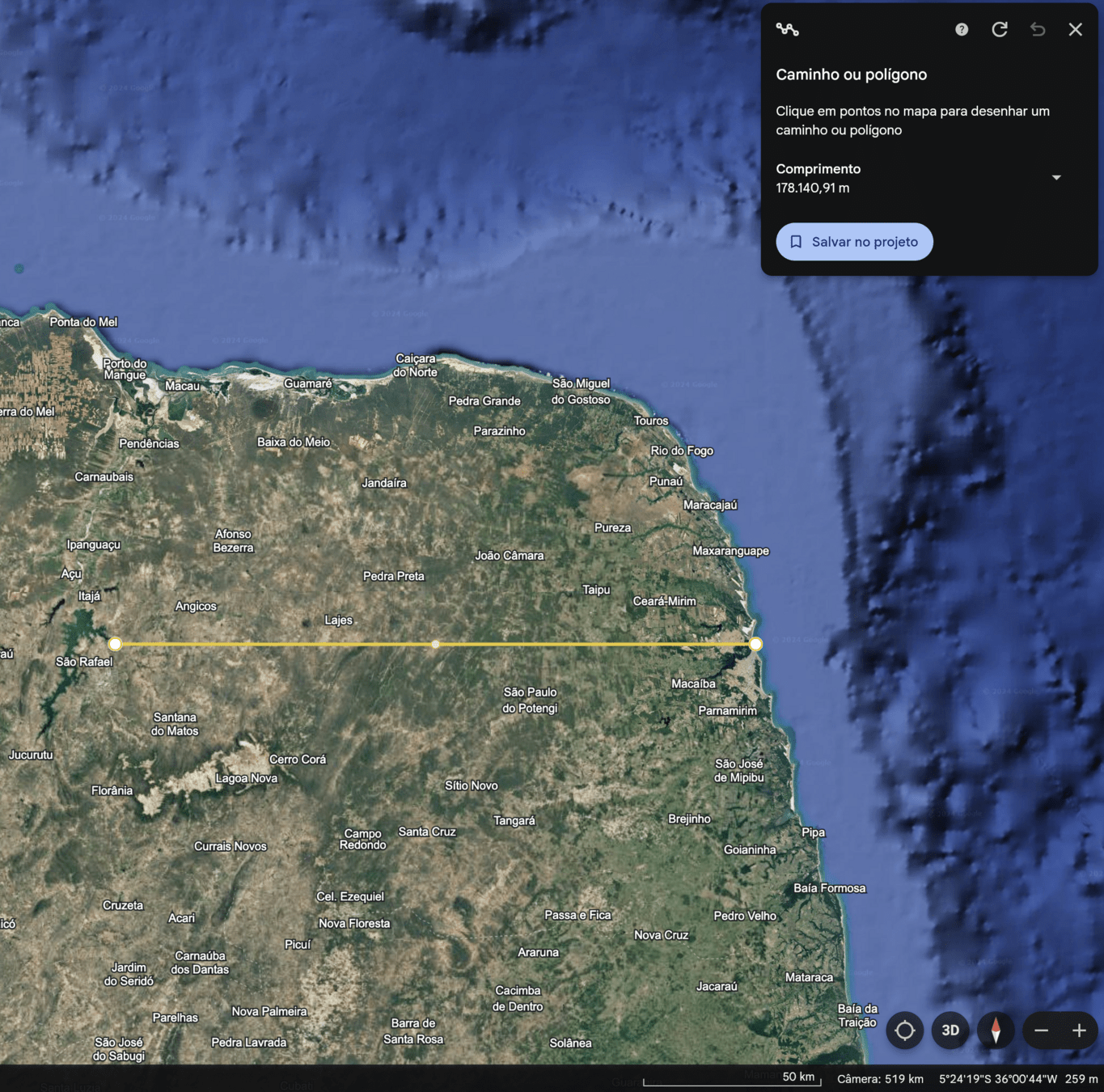
Sistema de Coordenadas Geográficas
O que mudou mais no trajeto AB, em amarelo, abaixo do equador? Longitude ou Latitude?


O movimento foi de:
- Leste para Oeste ?
- Oeste para Leste ?
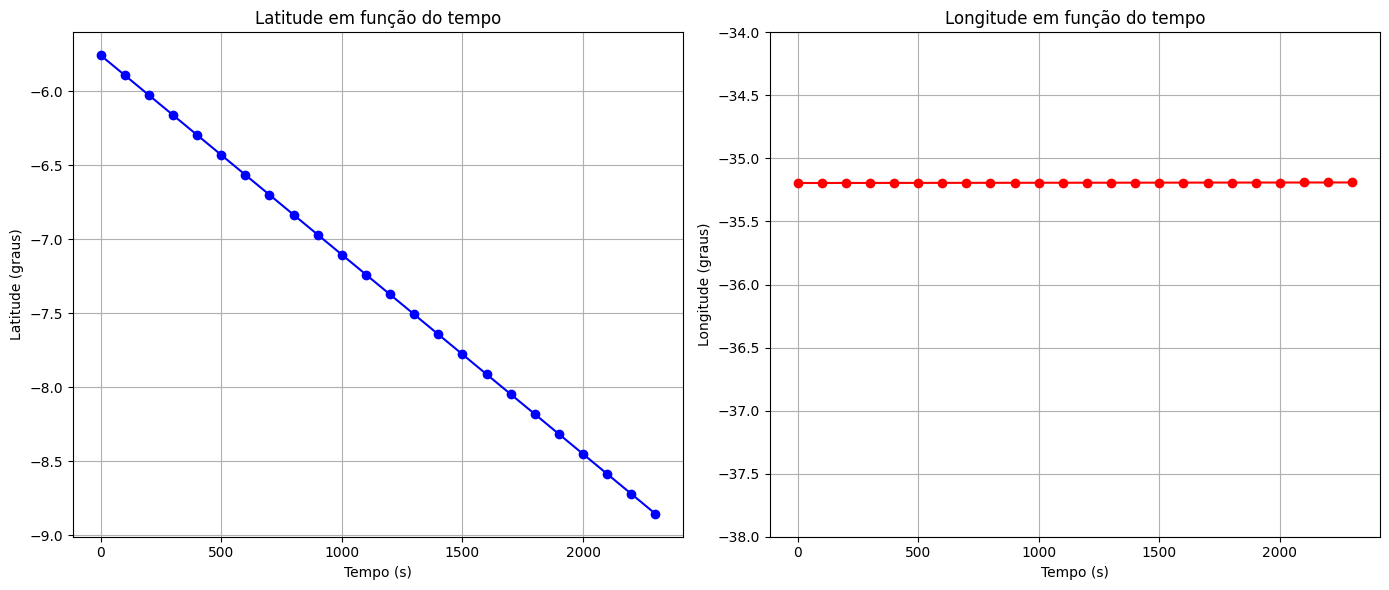
Gráficos de Latitude e Longitude em função do tempo de A para B.
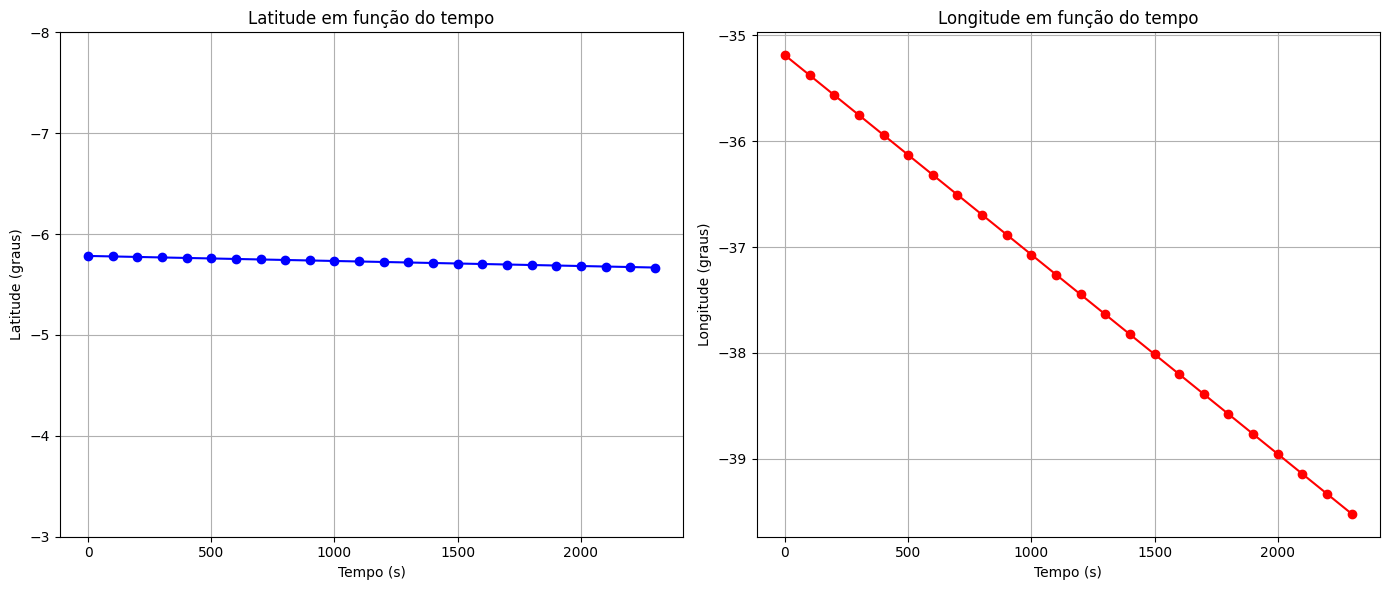
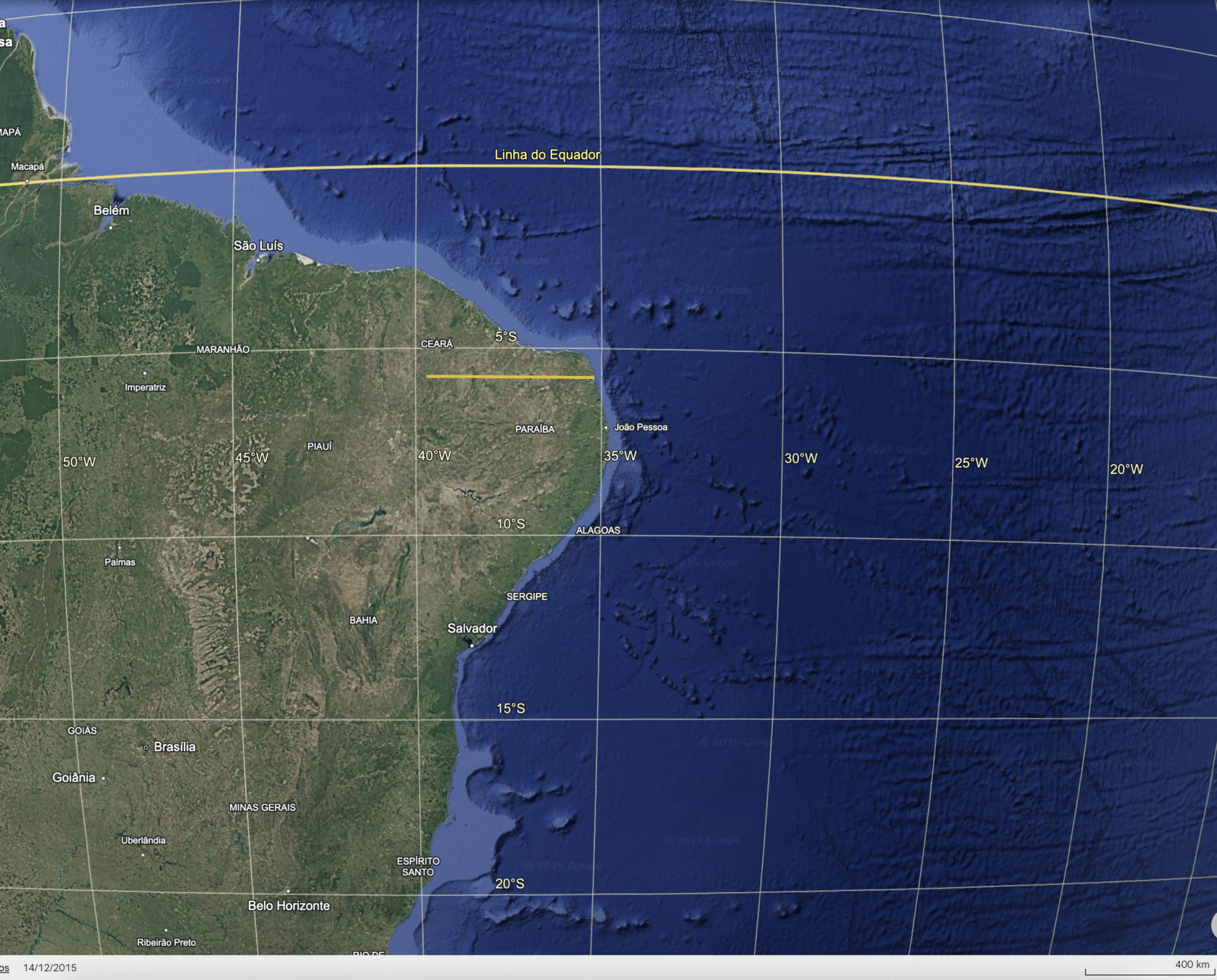
Sistema de Coordenadas Geográficas
O que mudou mais no trajeto AB, em vermelho? Longitude ou Latitude?
O movimento foi de:
- Norte para Sul ?
- Sul para Norte ?
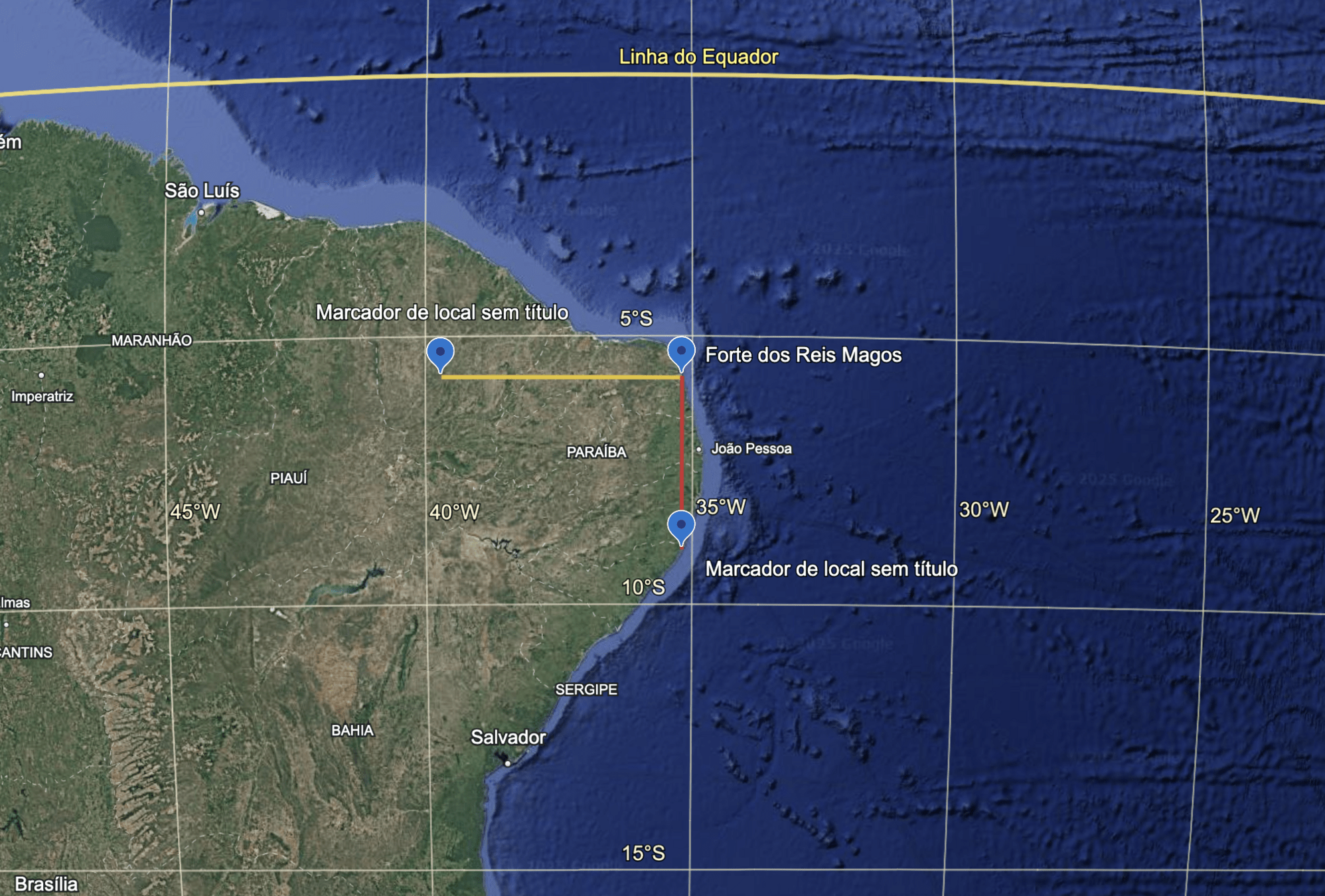


Gráficos de Latitude e Longitude em função do tempo de A para B.
Sistema de Coordenadas Geográficas
Como seriam os gráficos de Latitude e Longitude entre os dois pontos abaixo (BR101)?
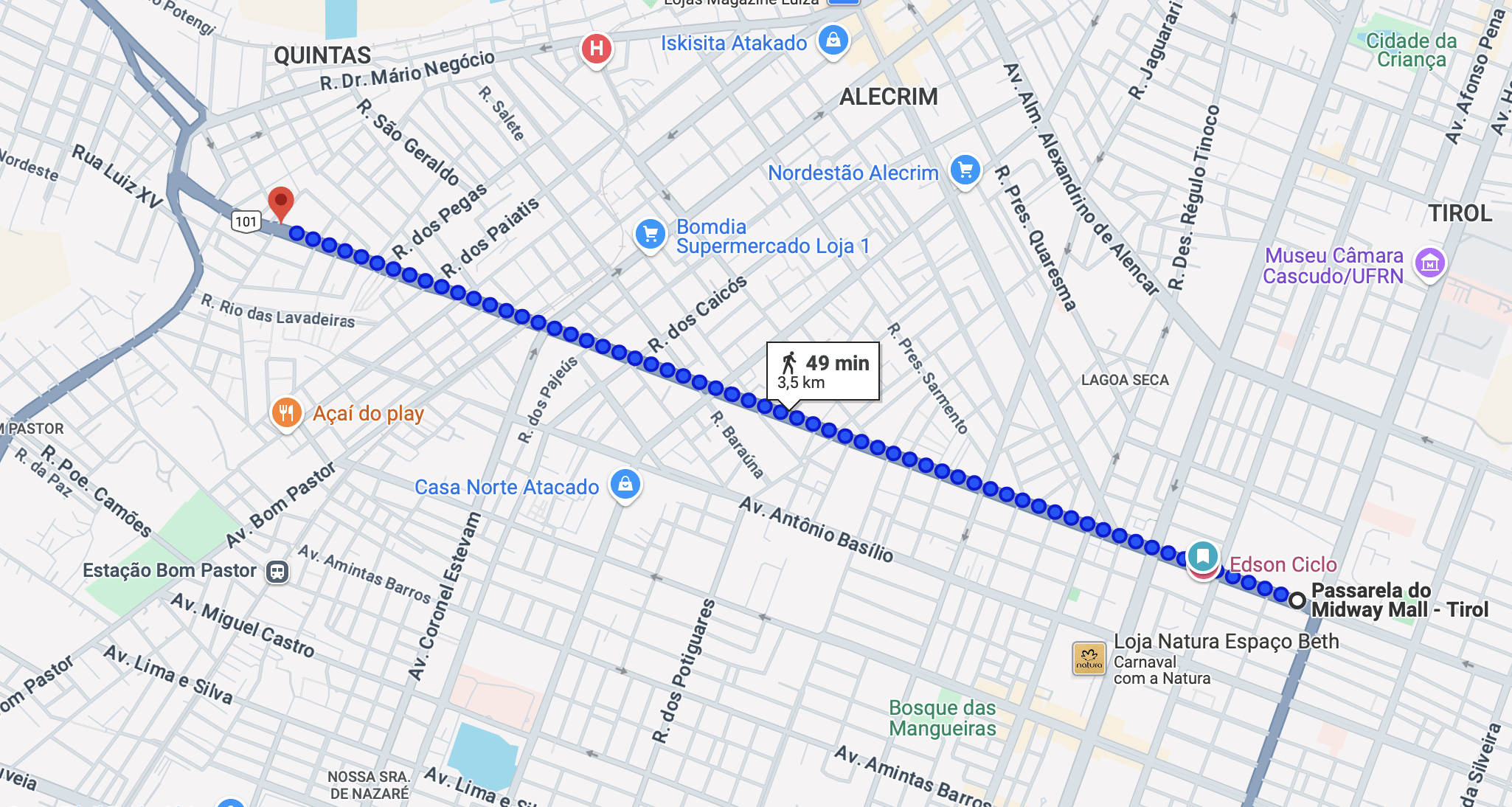
Ponto A:
Lat: -5,812595
Lon: -35,205303
Ponto B:
Lat: -5,801684
Lon: -35,235262
Fonte: https://www.google.com.br/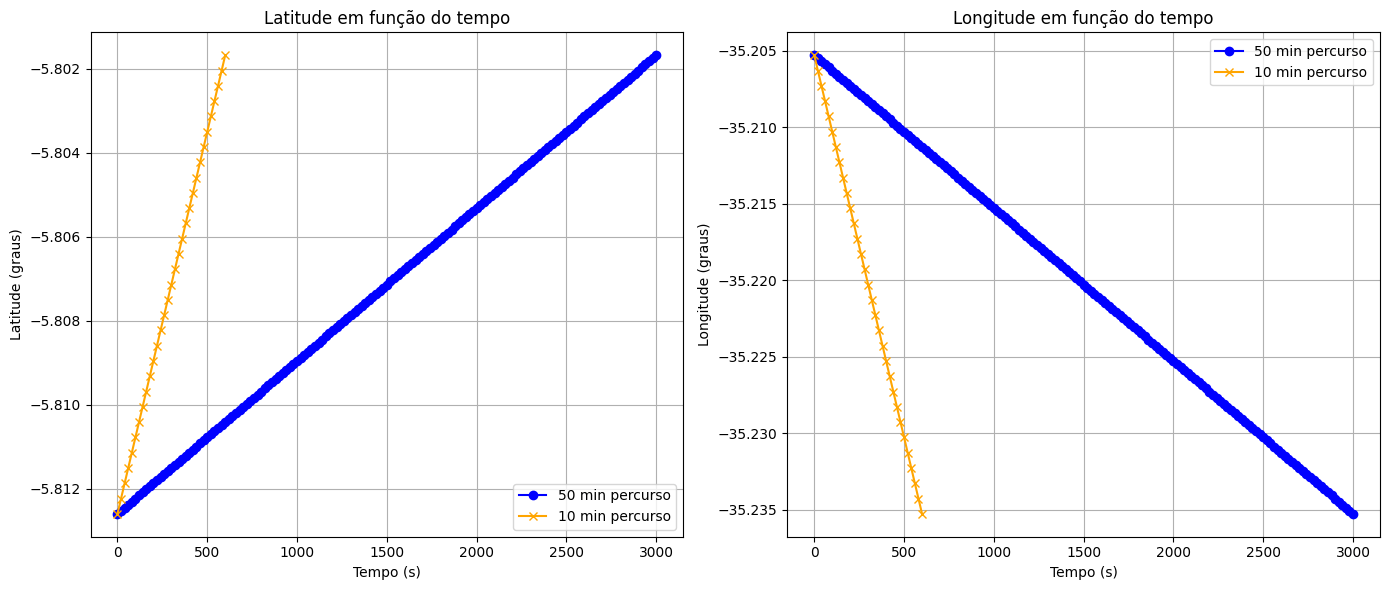
Qual o significado das linhas amarela e azul?
Estamos indo mais ao Norte ou mais ao Sul?
Estamos indo mais ao Oeste ou mais ao Leste?
Sistema de Coordenadas Geográficas
Considerando os gráficos de Longitude e Latitude. Qual seria o mapa correspondente, de ida e volta entre A e B, mas com uma paradinha em B antes
de retornar até A?
Fonte: Google Maps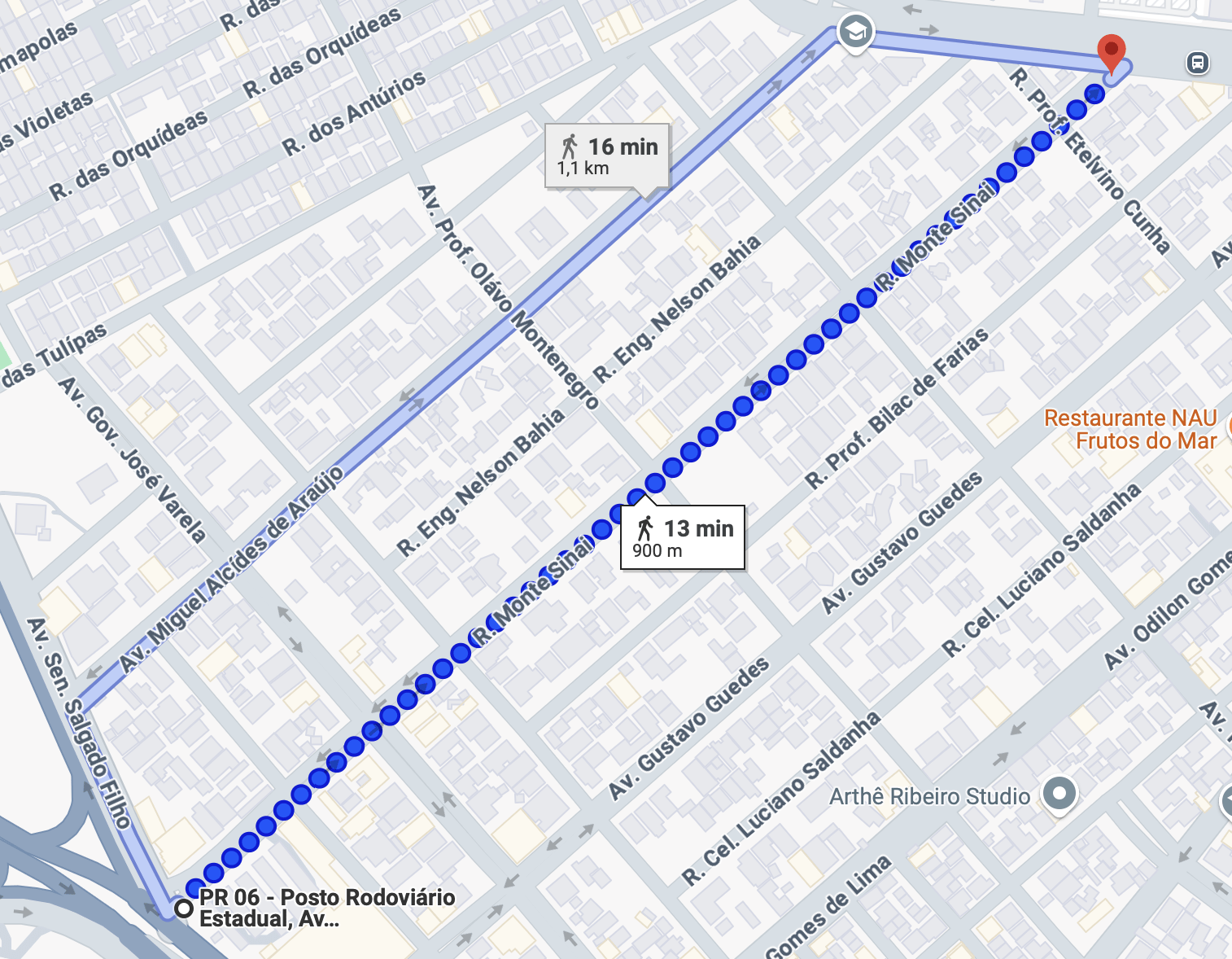
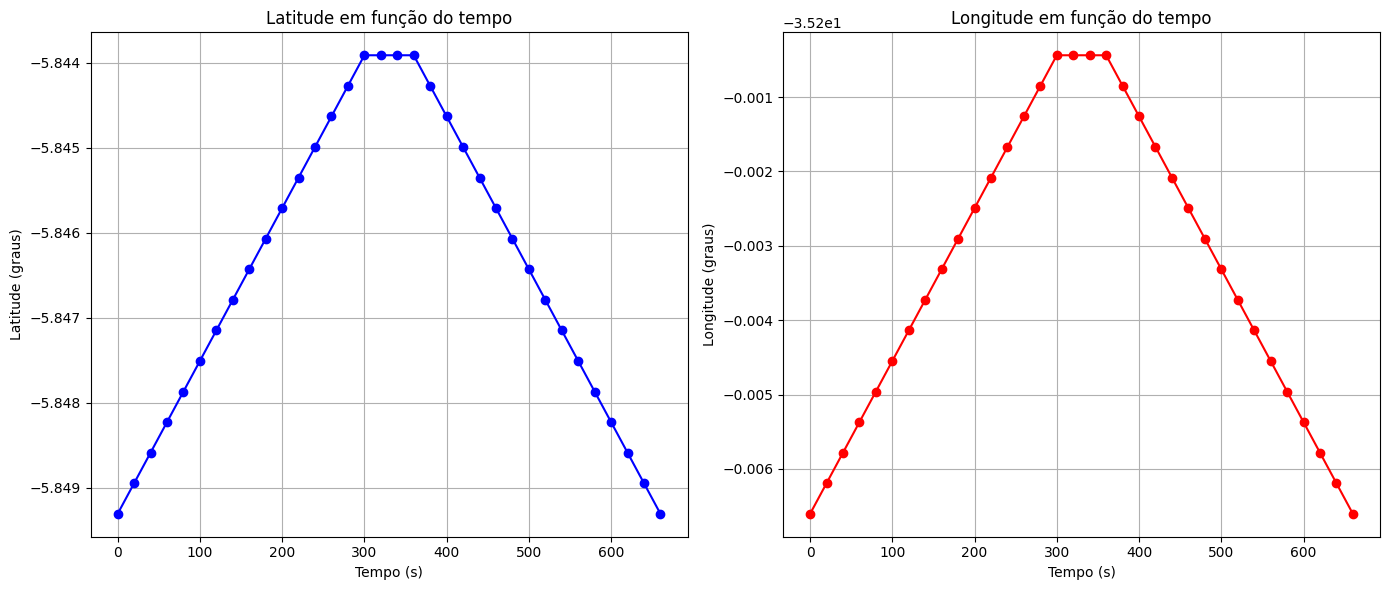
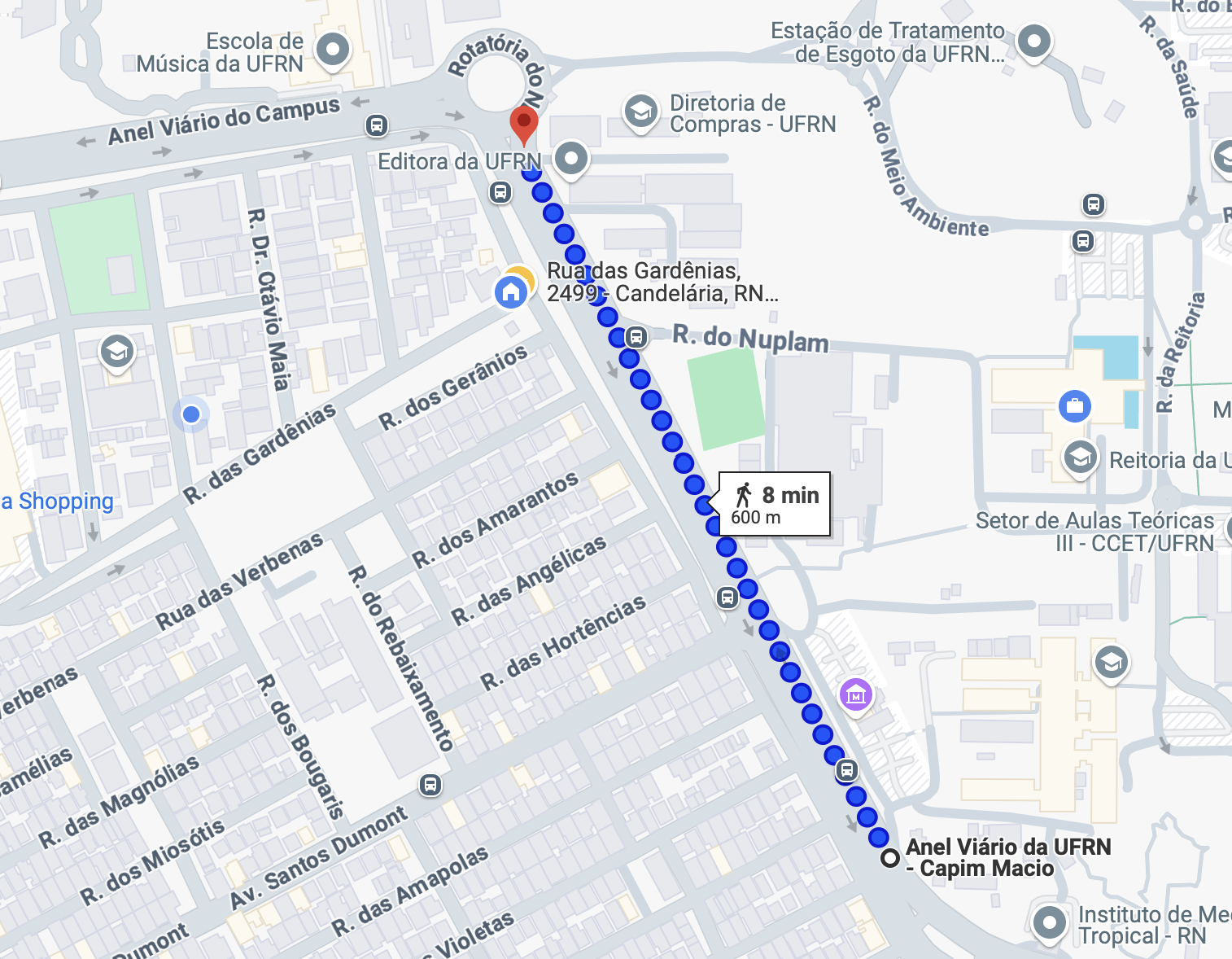
Mapa 1
Mapa 2
Fonte: Google MapsComo seria o gráfico do outro mapa?
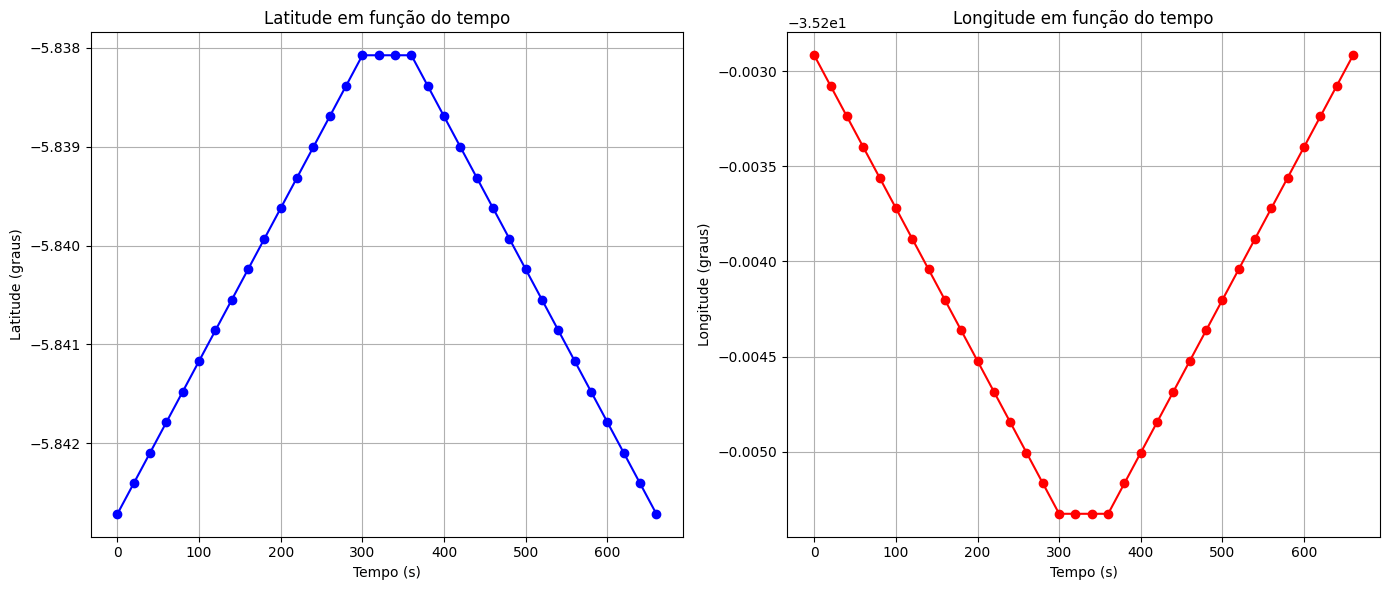
Experimento 1
Medindo a posição
Instale o software Phyphox e o GPS seu smartphone para medir as coordenadas de latitude e longitude.
Experimento 1 - Medindo a posição
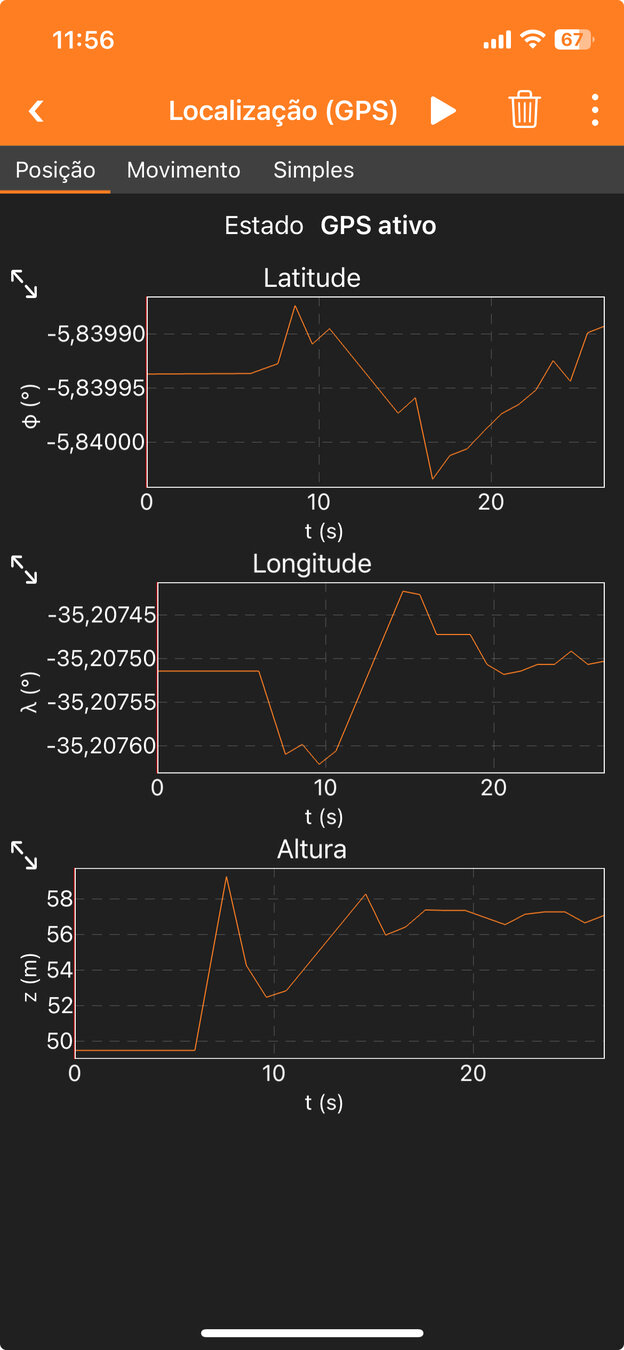

Localize a função: Localização GPS.
Aperte o botão: PLAY.
Movimente-se um pouco em linha reta.
Verifique os gráficos de latitude, longitude e altura.
Explore as informações das abas: posição, movimento e simples.
As flutuações das medidas cessam se o telefone permanecer no mesmo local por um curto período de tempo.
Experimento 1 - Medindo a posição

Ao se afastar alguns metros os números mudam para um novo valor estável.
As medida de latitude têm 8 algarismos significativos e a medida de longitude têm 9 algarismos significativos.
O aplicativo também fornece a altura, em metros.
Verifique que o Google Maps também fornece a altura quando você viaja com o GPS ligado.
1. Colete dados de localização ao caminhar em linha reta em ritmo constante.
2. Ao terminar a coleta você pode exportar os dados (vários formatos) ou salvá-lo.
3. Ao salvar a medida. Volte à tela principal do APP.
Experimento 1 - Medindo a posição

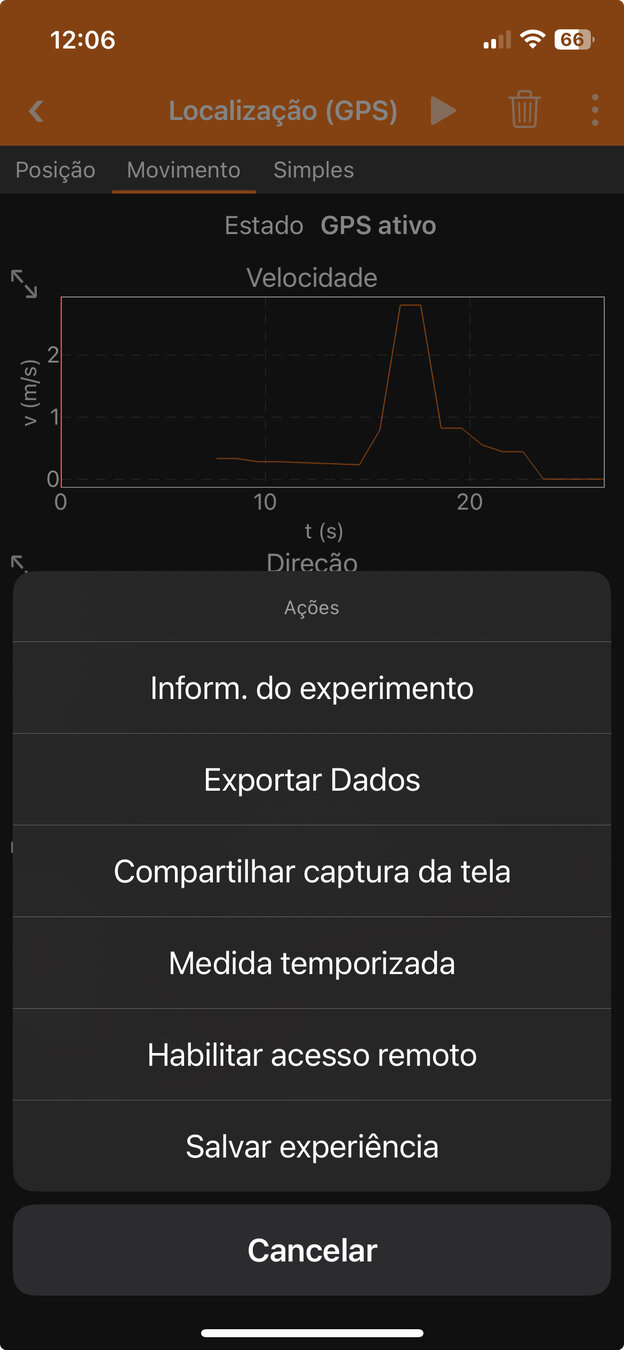
4. Usando o módulo "location" do phyphox, colete dados enquanto caminha em ritmo constante do ponto A ao ponto B e de volta ao ponto A.
- Você não precisa saber a distância exata;
- Você a determinará a partir do experimento.
- Uma distância de aproximadamente 100 metros deve ser suficiente.
- Para obter os melhores resultados, escolha um caminho sem grandes variações de elevação (sem grandes colinas).
Experimento 1 - Medindo a posição
5. Deixe o sensor localizar os satélites e refinar sua posição inicial no ponto A por 20 segundos antes de começar a caminhar até o ponto B.
6. Ao chegar ao ponto B, pare por aproximadamente 10 segundos no ponto B e depois caminhe de volta ao ponto A no mesmo ritmo constante.
7. Deixe o aplicativo coletar aproximadamente 10 segundos de dados em sua localização final antes de salvar e exportar para análise.
8. Capture a tela dos gráficos de latitude e longitude em relação ao tempo do aplicativo Phyphox. Exporte seus dados para um arquivo para uso posterior.
9. Determine a direção em que você estava caminhando (por exemplo, Nordeste, Sudoeste,
Experimento 1 - Medindo a posição
Exemplos
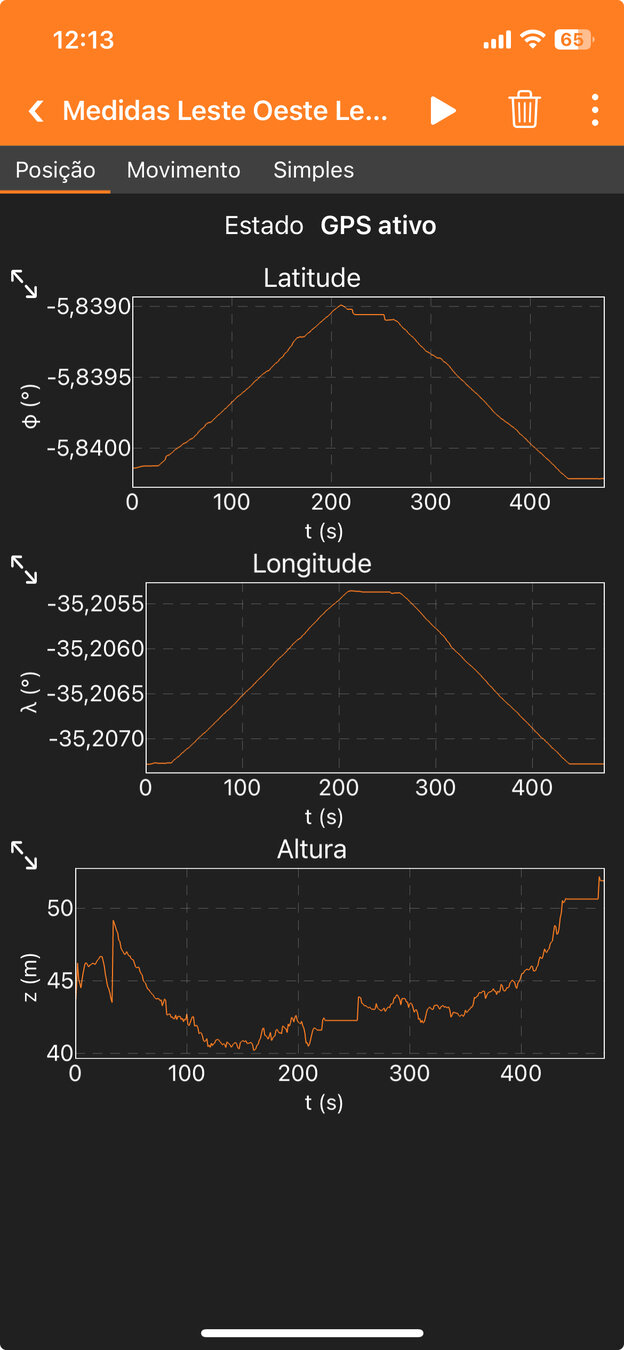
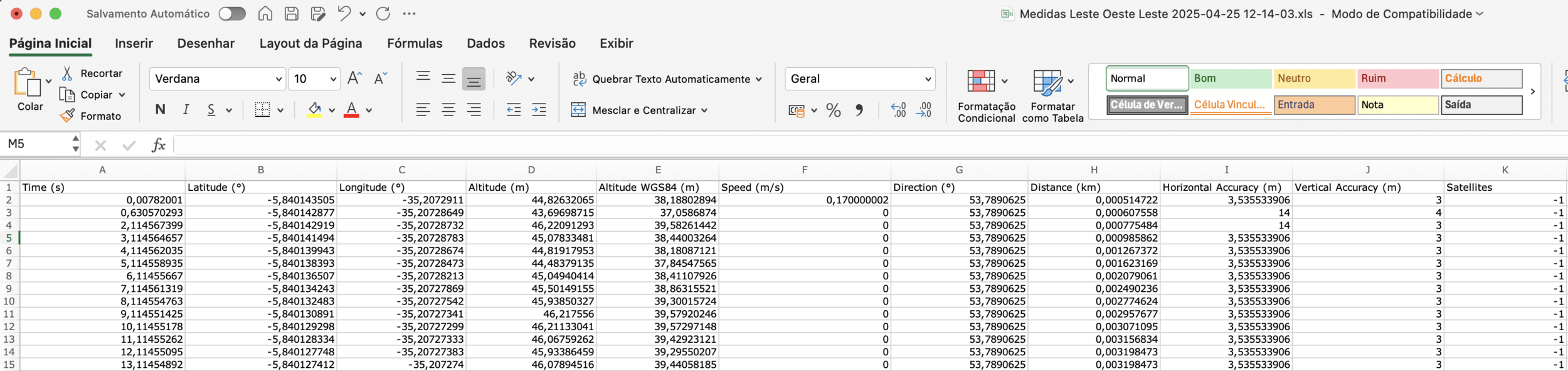
Experimento 1 - Medindo a posição
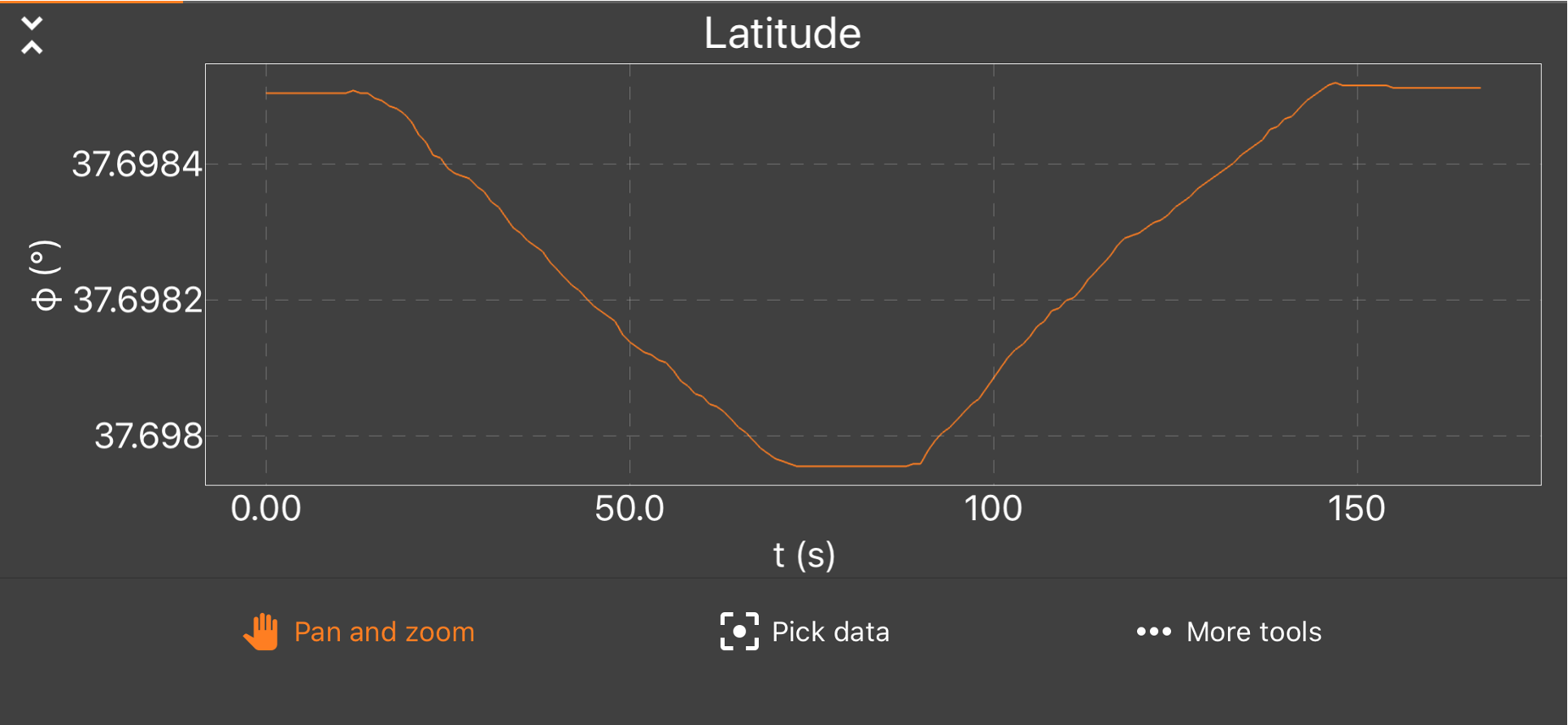

Em que direção a pessoa caminhou em t = 40 s?

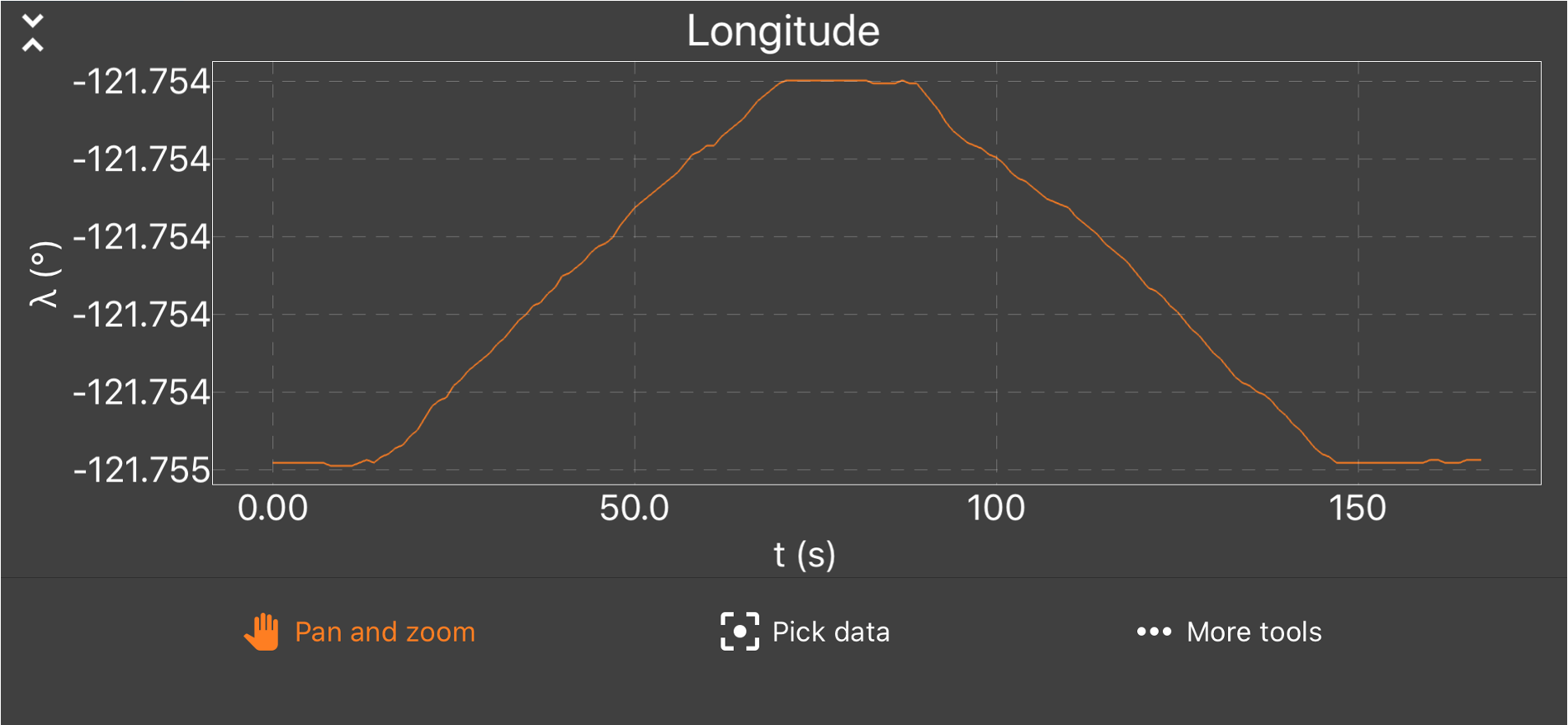
Norte - Nordeste - Leste - Sudeste - Sul - Sudoeste - Noroeste

Experimento 2
Construindo gráficos
Experimento 2 - Construindo gráficos
- Use os dados exportados e salvos do Experimento 1.
- Crie um gráfico de latitude versus tempo usando sua planilha favorita.
- Inclua rótulos em seus eixos.
- Escale os dados para permitir uma visualização eficaz.
- Indique a mudança de latitude em seu gráfico.
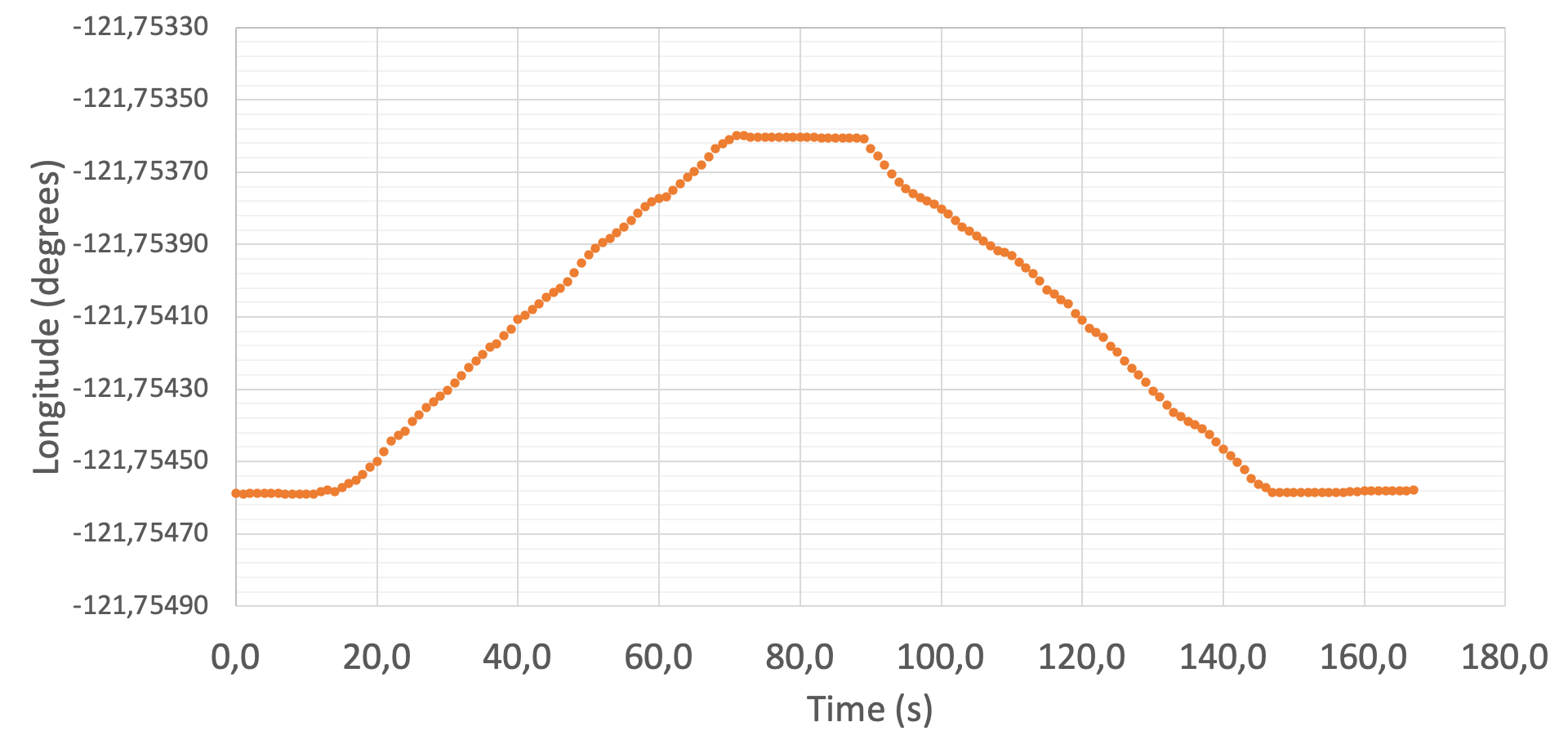
- Crie um gráfico de longitude versus tempo.
- Inclua rótulos em seus eixos.
- Escale os dados para permitir uma visualização eficaz.
- Indique a mudança de longitude em seu gráfico.
Experimento 2 - Construindo gráficos
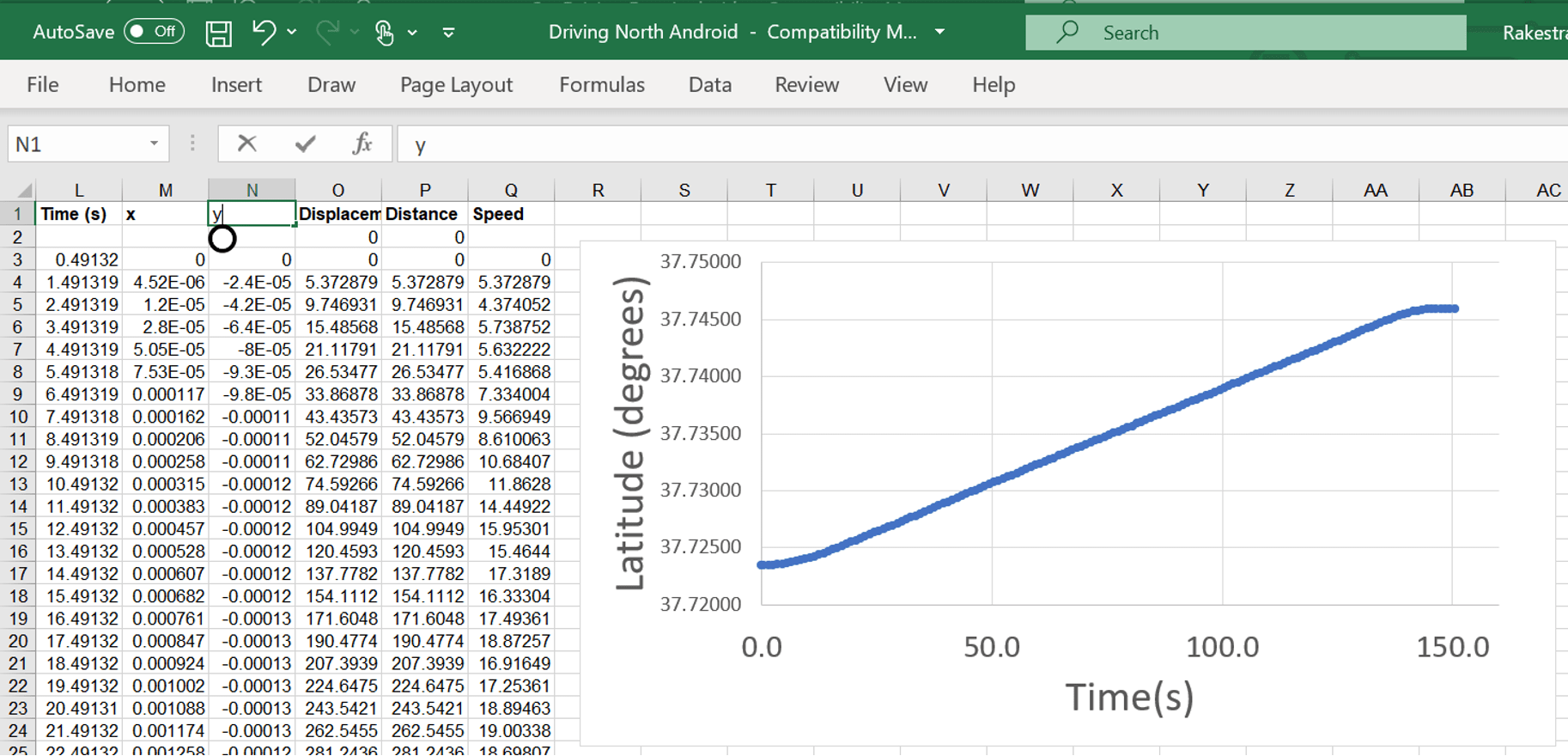
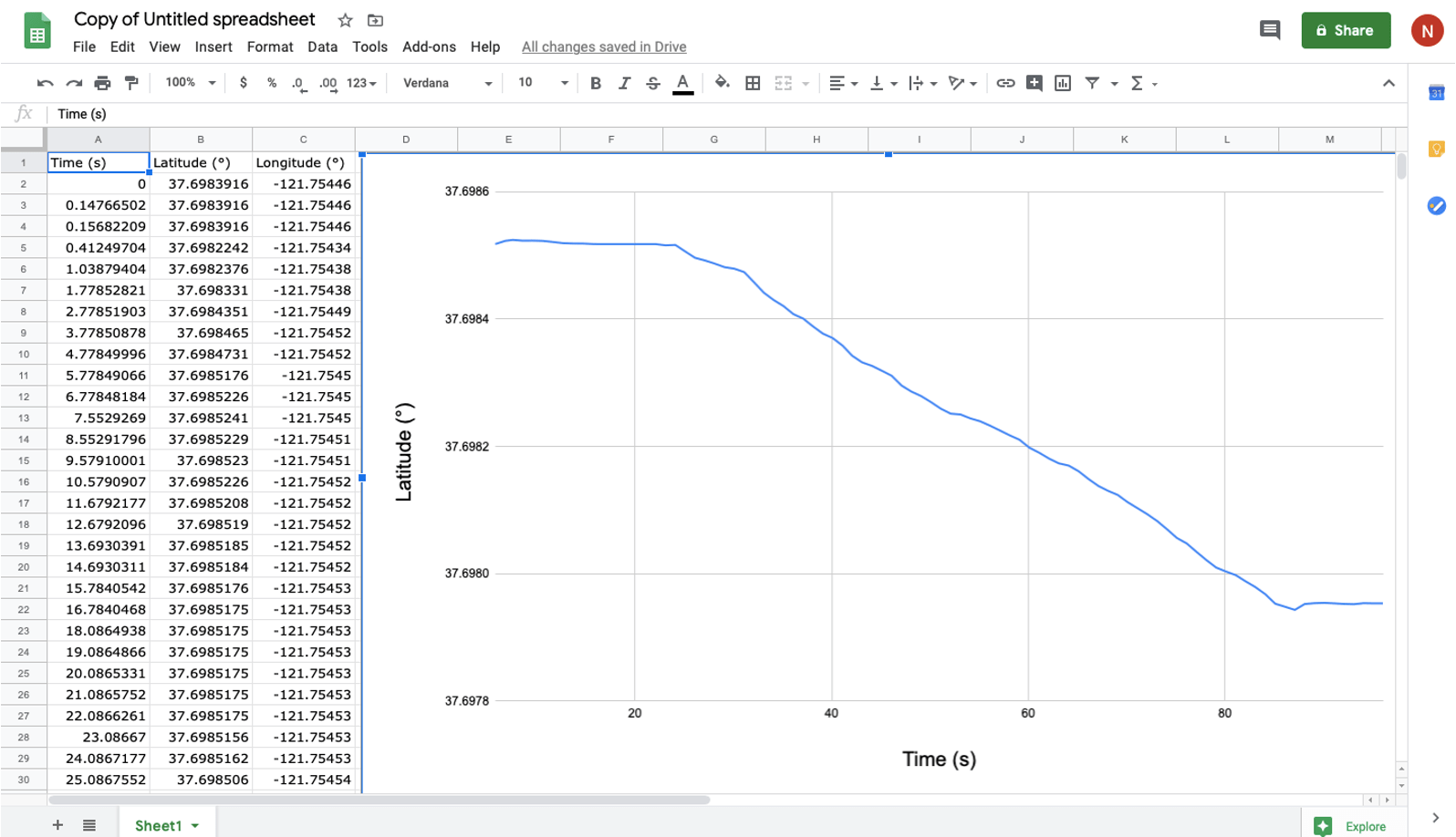
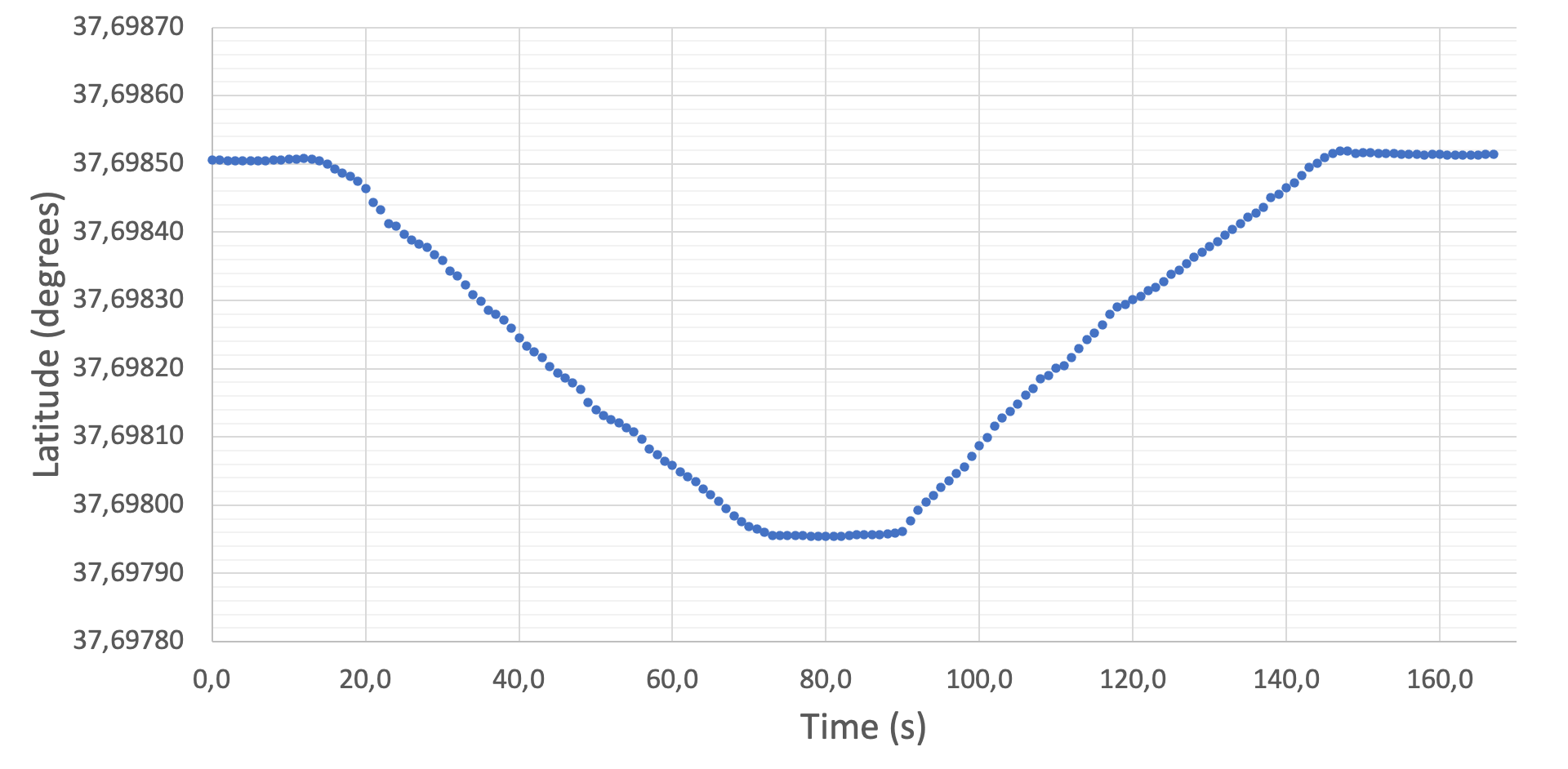


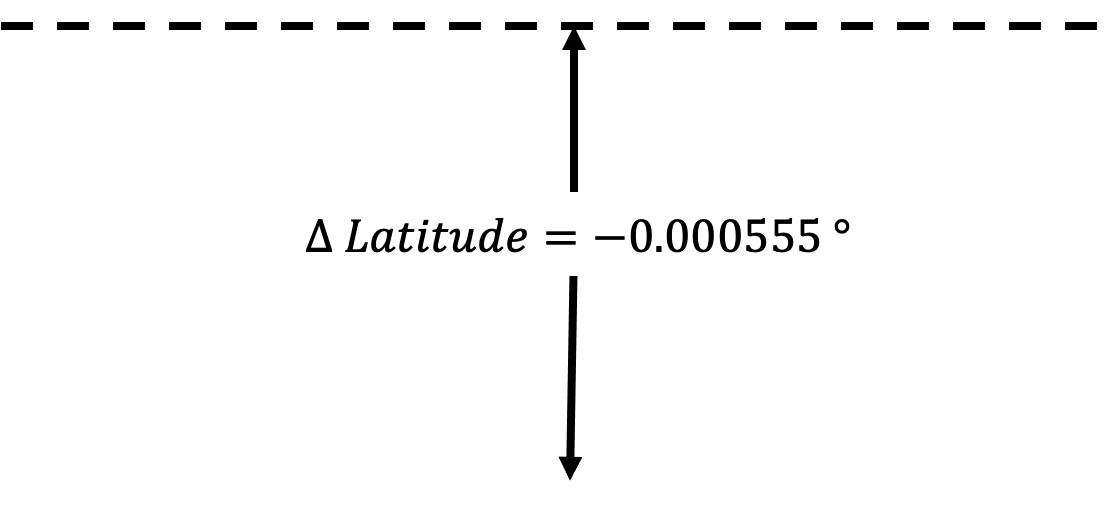




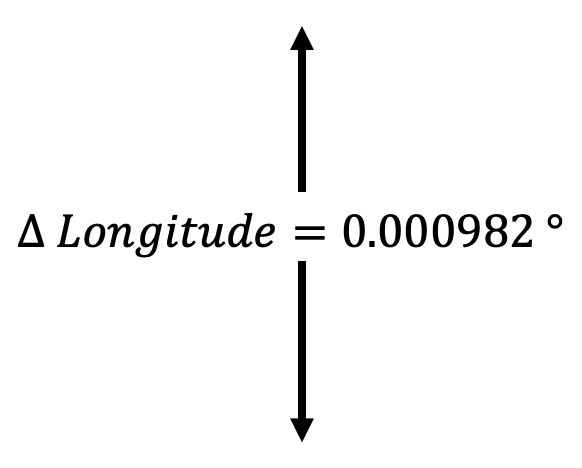

Experimento 3
Calculando distâncias a partir da Latitude e Longitude
Experimento 3. Cálculo de distância entre dois pontos.
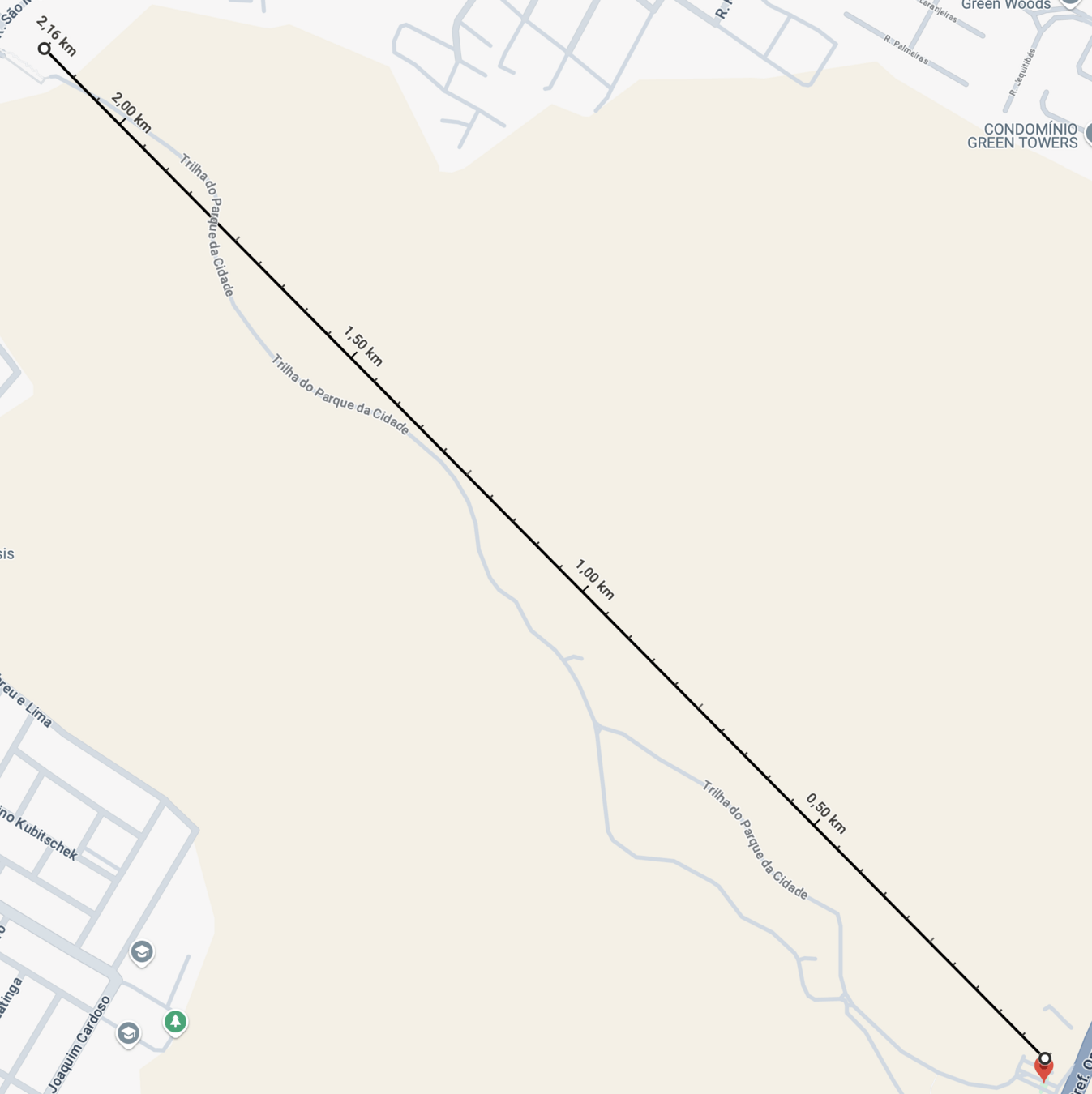


Parque da cidade
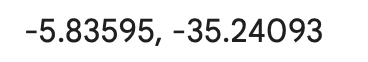
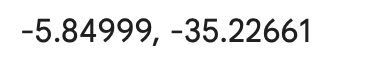
Como calcular a distância em sistema de coordenadas esféricas para pequenos deslocamentos a partir das coordenadas geográficas de longitude e latitude?
Calculamos a distância em um sistema de coordenadas esféricas para pequenos deslocamentos.
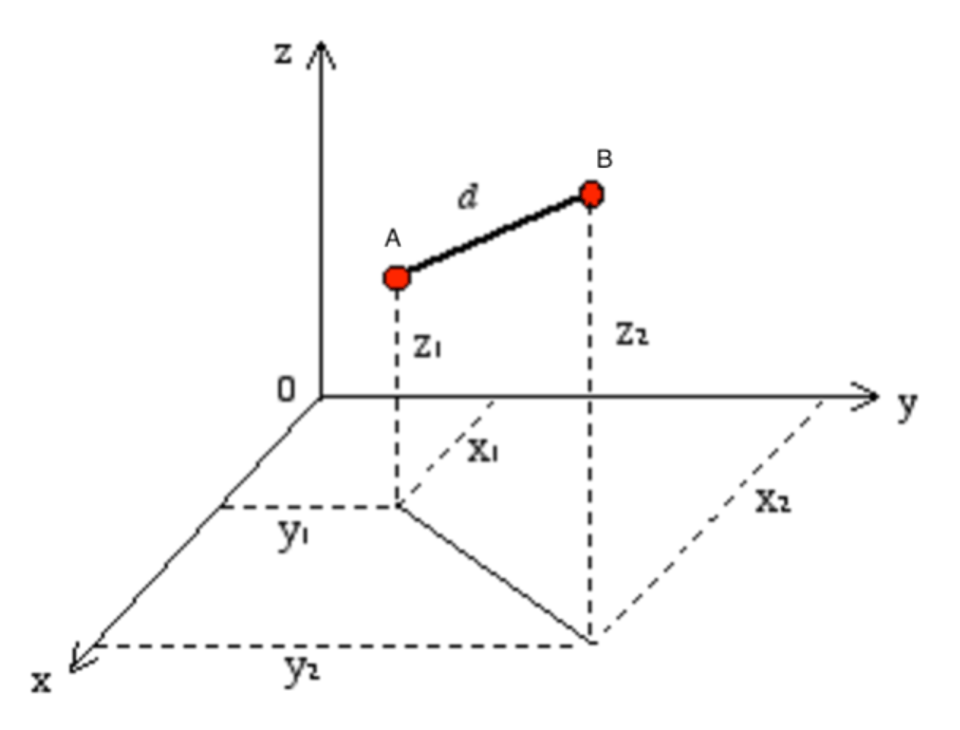
Coordenadas Euclidianas x Sistema de coordenadas esféricas
Nos slides seguintes vamos calcular essa distância ao irmos de A para B. (Oeste-Leste e Norte-Sul).
A
B
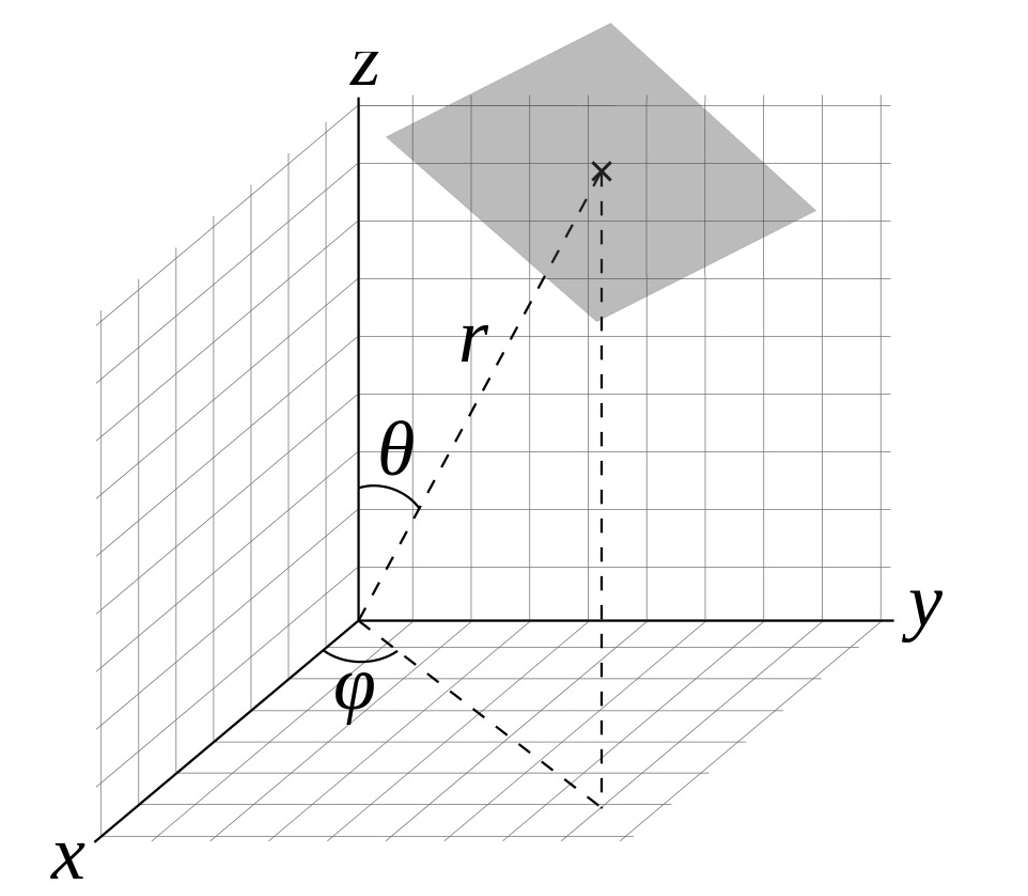
Vivemos em um planeta esférico, então precisamos usar esse sistema.
Em um sistema de coordenadas esféricas, um ponto é identificado por r, θ e φ.
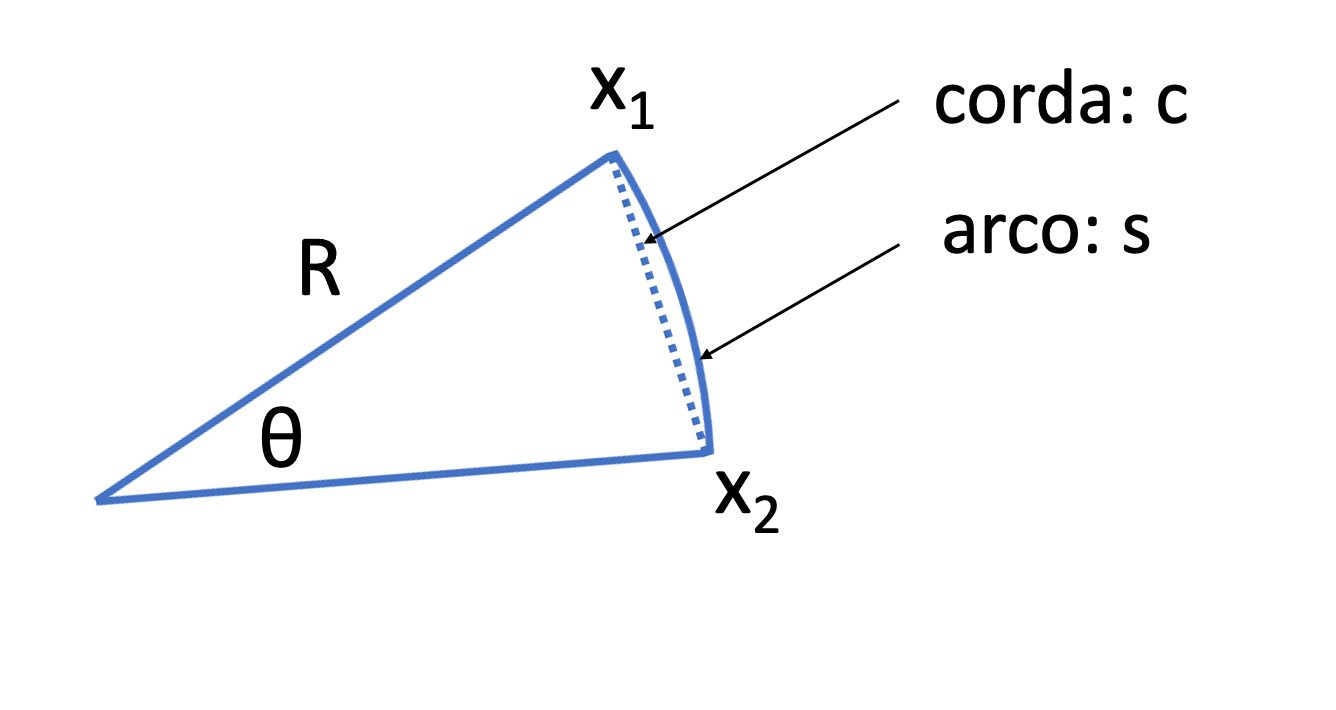
A distância entre \(x_1\) e \(x_2\) ao longo de uma linha reta é o comprimento da corda,
\(c = 2R \sin(\theta /2)\)
Experimento 3. Cálculo de distância entre dois pontos.
Vivemos em um planeta esférico, então precisamos usar esse sistema.

A distância entre \(x_1\) e \(x_2\) ao longo de uma linha reta é o comprimento da corda,
\(c = 2R \sin(\theta /2)\)
Distância entre \(x_1\) e \(x_2\) ao longo do arco é o comprimento do arco,
\(s = R\theta\)
Para \(R\) longo e pequeno \(\theta\), \(\sin(\theta) \approx \theta\).
Então, a corda \( c = 2R\sin(\theta/2) \approx R\theta = s\).
Experimento 3. Cálculo de distância entre dois pontos.
Vivemos em um planeta esférico, então precisamos usar esse sistema.

Conforme você viaja em uma linha de longitude, o raio do círculo é o raio da Terra, o ângulo que você cobre é \(Lat_2 – Lat_1\).
A distância percorrida ao longo da longitude
\(x \approx R(Lat_2-Lat_1)\).
Conforme você viaja em uma linha de latitude, o raio do seu círculo depende da sua longitude como \(R \cos(Lat)\). (Raio de latitude grande no equador e pequeno perto dos polos.)
O ângulo que você cobre é \(Long_2 – Long_1\). Na aproximação de ângulo pequeno:
Distância percorrida ao longo da latitude
\((y) ≈ R \cos(Lat) (Long_2 – Long_1)\)
Experimento 3. Cálculo de distância entre dois pontos.
Vivemos em um planeta esférico, então precisamos usar esse sistema.

Ao alterar a longitude e a latitude, combine os dois lados iguais do triângulo para obter a distância total percorrida:
Para localizações com \(Lat_1, Long_1\) e \(Lat_2, Long_2\), em graus:
onde R = 6,356 km é o raio da terra e \(\pi/180\) converte graus para radianos.
Experimento 3. Cálculo de distância entre dois pontos.
1. Determine a distância entre o ponto A e o ponto B usando a fórmula para calcular a distância entre dois locais usando sua calculadora.
Experimento 3. Cálculo de distância entre dois pontos.
Exemplo: DICA: Construa uma tabela no Excel para esses cálculos.
Ponto A: (-5,83595, -35,24093)
Ponto B: (-5,84999, -35,22661)

A
B


Experimento 3. Cálculo de distância entre dois pontos.
2. Utilizando os dados de latitude e longitude da planilha da Parte II:
- Calcule e plote o deslocamento em função do tempo.
- Indique o valor máximo do deslocamento no gráfico.
- Calcule e plote a distância total percorrida em função do tempo.
- Indique a distância total percorrida no gráfico e compare com o deslocamento máximo.
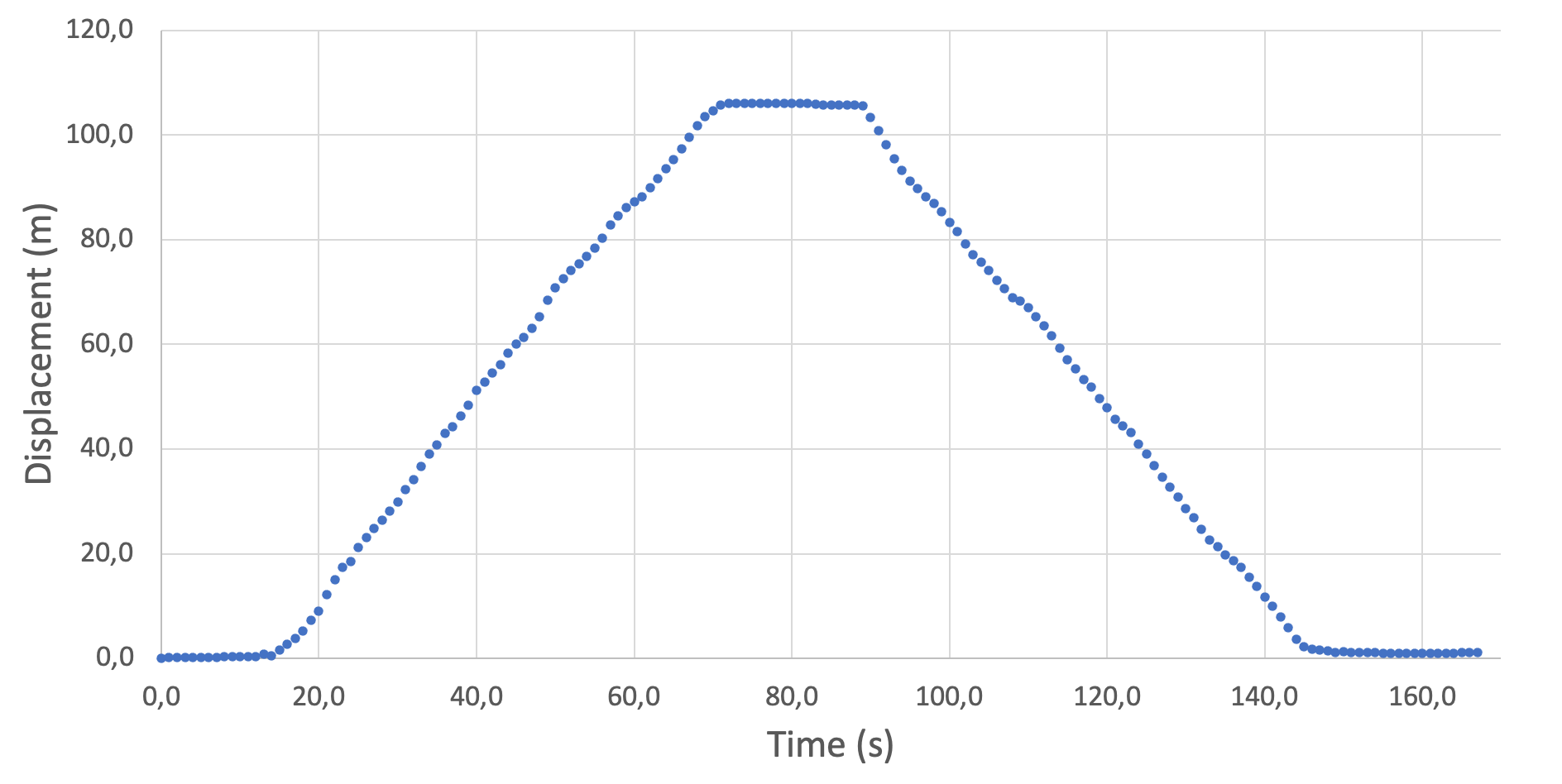
Exemplo: Os dados aqui não são os pontos A e B, anteriores.
A
B
C
VETOR
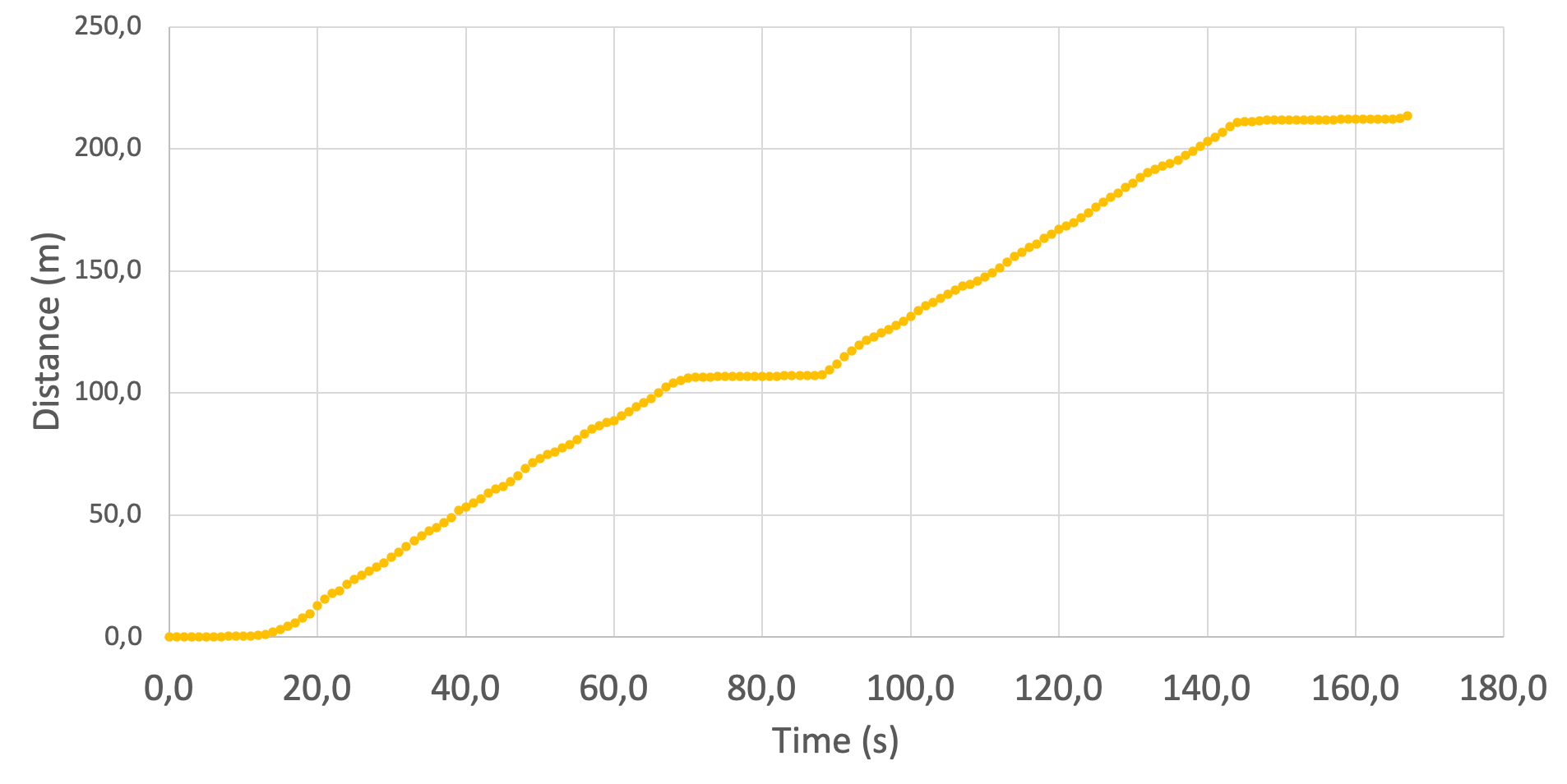
A
B
C
ESCALAR
Experimento 4
Calculando velocidade e rapidez
Experimento 4. Velocidade e rapidez
1. Usando os dados de deslocamento versus tempo:
# Calcule e plote a velocidade instantânea versus tempo.
# A velocidade instantânea pode ser calculada usando a variação da distância entre pontos de dados adjacentes e a variação do tempo associada.
2. Usando os dados de deslocamento versus tempo:
# Calcule e plote a rapidez instantânea versus tempo.
3. Usando os dados de deslocamento versus tempo:
# Calcule a velocidade média ao caminhar de A a B e depois de B a A.
- Use dados para períodos em que você caminhou a velocidade constante.
- A velocidade média pode ser determinada a partir da inclinação do gráfico de deslocamento versus tempo.
Experimento 3. Cálculo de distância entre dois pontos.
2. Utilizando os dados de latitude e longitude da planilha da Parte II:
- Calcule e plote o deslocamento em função do tempo.
- Indique o valor máximo do deslocamento no gráfico.
- Calcule e plote a distância total percorrida em função do tempo.
- Indique a distância total percorrida no gráfico e compare com o deslocamento máximo.

Exemplo: Os dados aqui não são os pontos A e B, anteriores.
A
B
C
O deslocamento \(\Delta x\) é um vetor e sua magnitude e sentido é lido ao longo do eixo deslocamento no gráfico ao lado.
No exemplo do slide anterior \(\Delta x = 2225 \text{ m}\) e esse valor é igual à distância percorrida.