Aula 07

Fundamentos da Mecânica

Prof. Ronai Lisbôa

BCT - ECT - UFRN

Objetivos

Enunciar a Segunda Lei de Newton

Enunciar a Terceira Lei de Newton

Enunciar a Primeira Lei de Newton

Aplicar as Leis de Newton me problemas clássicos:

Plano inclinado.

Máquina de Atwood.

Movimento horizontal.

Movimento vertical.

Bibliografia.

Tipler - Cap. 4

Seções 4.1 a 4.8 ( todas!)

- Faça os exercícios resolvidos.

A primeira lei de Newton

Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que seja forçado a mudar aquele estado por forças imprimidas sobre ele.

Corpus omne perseverare in statu suo quiscendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.

Fonte: http://astroacademy.org.uk/resources/collisions/

Aqui está um referencial inercial(*),

(*) A estação espacial internacional está girando em órbita, mas o evento ocorre num intervalo tal que a estação é considerada um referencial inercial.

\frac{2\pi \Delta t}{T}<<1

A primeira lei de Newton. Os quadros de referenciais inerciais.

Uma conseqüência da Lei da Inércia é que não é possível deduzir das medições realizadas inteiramente em um referencial o movimento desse referencial em relação a outros referenciais.

\vec v=\vec 0
\vec v=\vec c

A primeira lei de Newton. Os quadros de referenciais inerciais.

Observando a superfície do café ou a chave caindo você não será capaz de dizer se está em repouso ou se movendo à velocidade constante. Exceto, claro se houver uma variação da velocidade do avião!

O efeito é o mesmo daquele se você estivesse tomando o café ou deixando a chave cair enquanto está em uma cafeteria.

A primeira lei de Newton. Os quadros de referenciais inerciais.

As leis do universo são as mesmas em todos os referenciais inerciais, movendo-se a uma velocidade constante entre si.

As leis do universo são as mesmas em todos os referenciais inerciais, e não existe um referencial que esteja "em repouso" em algum sentido absoluto.

Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que seja forçado a mudar aquele estado por forças imprimidas sobre ele.

A segunda lei de Newton

A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção da linha reta na qual aquela força é imprimida.

Mutationem motus proportionalem esse vi motrici impressa, fieri secundum lineam rectam qua vis illa imprimitur

A Segunda Lei de Newton

A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção da linha reta na qual aquela força é imprimida.

Se há aceleração, então, a partícula não é livre.

Observa-se experimentalmente:

A força tem  a direção da linha reta entre as partículas.

A força é proporcional à aceleração.

Se há aceleração existe uma interação de uma partícula com outra.

O movimento que não é natural é forçado.

\vec F_{12}
\vec v
\vec v
\vec v
\vec v
\vec a

As interações ocorrem entre um par de objetos.

As interações fazem os objetos acelerarem (variação da velocidade no tempo).

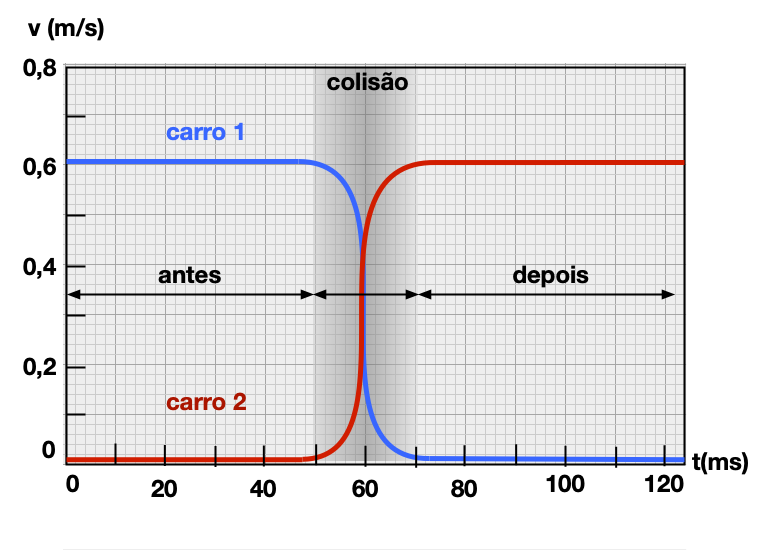
A colisão faz:

O carro 1 sair do repouso.

O carro 2 entrar em repouso.

Antes a velocidade é nula. Depois é constante.

Antes a velocidade é constante. Após é nula.

Movimento natural

Movimento forçado

Fonte: http://www.iwant2study.org

A Segunda Lei de Newton

Em um referencial inercial o movimento forçado é aquele em que:

LINK.

Carro 1

Carro 2

Para um grupo de objetos todos feitos do mesmo material, é mais difícil mudar o movimento de objetos maiores do que o movimento de objetos menores.

Os objetos maiores colocam mais resistência quando tentamos variar sua velocidade.

A inércia é uma medida da tendência de um objeto a resistir a qualquer variação em sua velocidade.

\text{inércia}\propto \frac{1}{|\Delta v|}

A Segunda Lei de Newton

\text{massa}\propto \frac{1}{|\Delta v|}
\Rightarrow

A inércia é uma propriedade intrínseca do objeto e depende do tipo e da quantidade de material do objeto.

A Segunda Lei de Newton

Ao produto da massa inercial pela aceleração denominamos por força resultante.

\vec a \propto \vec F
\vec v_f
\vec F_{vc}
m
m
\vec v_i
\vec F_{\text{ por\,você\, na \,caixa}}

Fonte: https://svgsilh.com/

A mudança de movimento (aceleração) é proporcional à força motora imprimida, e é produzida na direção da linha reta (direção da força) na qual aquela força é imprimida.

\vec a = \frac{\vec F}{m}
\vec F = m\vec a

Se a massa inercial do objeto é constante (partícula):

\vec F_R=m \vec a

é chamada de equação de movimento para o objeto porque permite determinar o movimento do objeto.

\vec a
\vec F_{R}
m

A aceleração do objeto pode ser calculada para qualquer tempo t,

\vec a = \frac{\vec F_R}{m}

A Segunda Lei de Newton

Ao produto da massa inercial pela aceleração denominamos por força resultante.

Ao produto da massa inercial pela aceleração denominamos por força resultante.

A terceira lei de Newton

A toda ação há sempre oposta uma reação igual, ou, as ações mútuas de dois corpos, um sobre o outro, são sempre iguais e dirigidas a partes opostas.

Actioni contrariam semper & aqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aquales & in partes contraria dirigi.

Se você empurrar uma caixa pelo chão, a caixa empurra você com uma força de igual magnitude, na mesma direção e no sentido oposto.

m
\vec F_{\text{ por\,você\, na \,caixa}}
\vec F_{\text{ pela\,caixa\, em \,você}}

Pode um objeto inanimado, como uma caixa, exercer uma força e, se sim, como sabemos que essa força existe? SIM. PODE, pois o objeto se deforma e deformações estão associadas à forças!

A Terceira Lei de Newton

ATENÇÃO. Note que você aplica a força na caixa.  A caixa aplica um força em você.

ATENÇÃO. O par de interação atua em objetos diferentes!

Fonte: https://svgsilh.com/

\vec F_{21}=-\vec F_{12}

Sempre que dois objetos interagem, exercem sobre si forças iguais em magnitude e direção, mas opostas em sentido.

(\vec F_{21}+\vec F_{12})=\vec 0

A força que Konishiki Yasokichi (b.1963) exerce sobre o menino é a mesma força que o menino exerce sobre Konishiki Yasokichi.

Fonte: https://hipwallpaper.com

A terceira lei de Newton

O par de ação e reação são forças internas e se cancelam dentro do sistema. Assim, elas não são capazes de alterar o movimento do centro de massa sistema.

A Terceira Lei de Newton

Fonte: https://youtu.be/UYb4rs013ZQ?si=C-XdsNdMcEgAgpLD
Fonte: https://youtu.be/QsGMKv8Lrew?si=0k0m-Gukzjo-JZvY
Fonte: https://www.youtube.com/embed/ZkVU-bj9bDk

A equação de movimento permite obter toda a história do movimento do objeto:

Vamos obter as funções velocidade e posição:

Integrando de uma velocidade inicial em \(t_i\) = 0 a uma velocidade final em \(t_f\) = t:

\vec v_f= \vec v_i+ \frac{\vec F_R}{m}t
\vec x_f= \vec x_i+ \vec v_i t+ \frac{\vec a}{2} t^2
\vec a = \frac{\vec F_R}{m}
\frac{d\vec v}{dt} = \frac{\vec F_R}{m}
d\vec v= \frac{\vec F_R}{m}dt
\int d\vec v= \int \frac{\vec F_R}{m}dt

Reescrevendo:

\frac{dx}{dt}= \vec v_i+ \frac{\vec F_R}{m} t
dx= (\vec v_i+ \frac{\vec F_R}{m} t)dt
\int dx= \int (\vec v_i+ \frac{\vec F_R}{m} t)dt

Integrando de uma posição inicial em t = 0 a uma posição final em t = t:

A equação de movimento

porque essas forças se cancelam aos pares. As massas se aproximam, mas o centro de massa fica imóvel.

\vec a_1

As forças internas ao sistema não são capazes de alterar o movimento do centro de massa sistema.

As forças internas

\vec F_{21}=-\vec F_{12}
(\vec F_{21}+\vec F_{12})=\vec 0
\vec a_2
m_2
\frac{a_1}{a_2}=-\frac{m_2}{m_1}
a_1< a_2
\frac{\Delta v_1}{\Delta v _2}=-\frac{m_2}{m_1}
\Delta v_1< \Delta v_2
\vec a_1
\vec a_2
m_2
c.m.

As mudanças de movimento são inversamente proporcionais às massas:

porque

m_1> m_2 \,.
\sum F_{int} = \vec 0
F_{21}=-F_{12}
m_1 a_{1}=-m_2 a_{2}
\vec F_{21}
m_1
\vec F_{12}
\vec F_{21}
m_1
\vec F_{12}

Simulação

A soma vetorial de todas as forças exercidas em um objeto é igual à força resultante sobre o objeto.

\vec F_{1c}+\vec F_{2c}=

A magnitude da velocidade da caixa é \(\Delta v_c = \frac{F_{Rc}}{m} \Delta t\).

F_{Rc} = +2\text{ N}
\vec F_{Rc}
\sum_{i=1}^n \vec F_{ic}
=\vec F_{Rc}=m\vec a
F_{2c} = -8\text{ N}
F_{1c} = +10\text{ N}
\vec F_{1c}
\vec F_{2c}
equivalente

O princípio de superposição

A aceleração da caixa é \(\frac{\Delta v_c}{\Delta t} = \frac{F_{Rc}}{m}\).

Exemplo 1

Considerar a situação em que três cordas são amarradas em um ponto comum, com uma equipe puxando cada corda. Suponha que a equipe 1 esteja puxando para o oeste com uma força de 2750 N, e que a equipe 2 esteja puxando para o norte com uma força de 3630 N. Uma terceira equipe pode puxar de tal forma que o cabo de guerra com três equipes termine empatado, ou seja, nenhuma equipe consiga mover a corda? Se sim, qual é o módulo e o sentido da força necessária para realizar isso?

\vec F_1
\vec F_2
\vec F_3
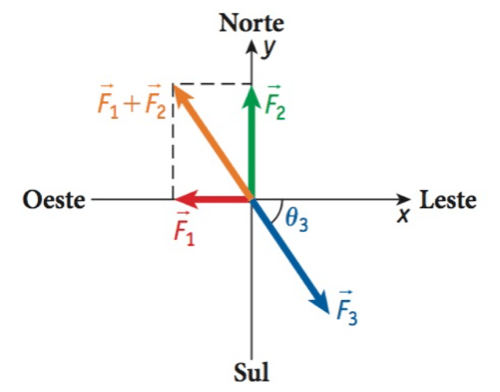
Fonte: Wolfgang

Exemplo 2

Um ginasta de massa 55 kg está pendurado verticalmente em um par de argolas paralelas.  Se as cordas que sustentam as argolas são verticais e presas a teto diretamente acima, qual é a tensão em cada corda?

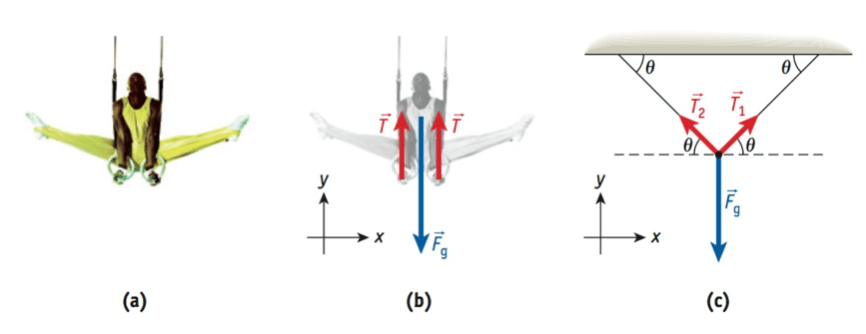
Fonte: Wolfgang
Fonte: https://images.app.goo.gl/

Exemplo 3

Que força precisamos aplicar à extremidade livre da corda 1 para manter o sistema em equilíbrio estático?

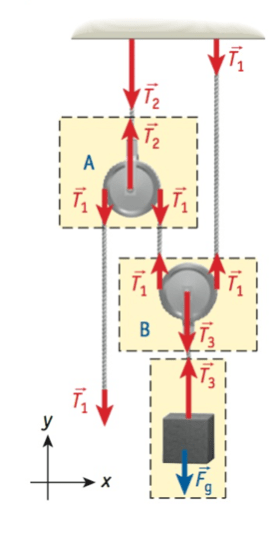
Fonte: Wolfgang

Exemplo 4

Um praticante de skibunda (massa de 72,9 kg, altura de 1,79 m) está descendo uma montanha de areia com um ângulo de 22° em relação à horizontal. (a) Se pudermos desprezar o atrito, qual é sua aceleração? (b) Supondo que tenha partido do repouso, qual a sua velocidade na base da inclinação se a altura da inclinação é de 10 m?

Exemplo 5

Neste problema clássico, uma massa pendurada gera uma aceleração para uma segunda massa sobre uma superfície horizontal (Figura). Um bloco, de massa \(m_1\), está sobre uma superfície horizontal sem atrito e é conectado por meio de uma corda sem massa (por questão de simplicidade, orientada no sentido horizontal) que passa sobre uma polia sem massa para outro bloco, com massa \(m_2\), pendurada na corda. (a) Qual a aceleração do sistema? (b) Quais as trações? (c) Quanto tempo leva para \(m_2\) tocar o chão se caiu de uma altura igual h e foi solto a partir do repouso?

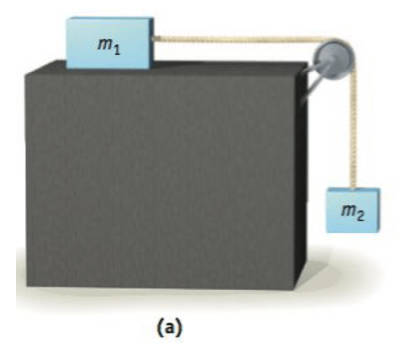
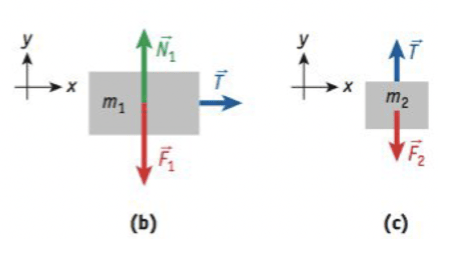
Fonte: Wolfgang
h

Exemplo 6

A máquina de Atwood consiste em dois pesos pendurados (com massas \(m_1\) e \(m_2\)) conectados por uma corda que passa por uma polia. Por enquanto, consideramos um caso sem atrito, em que a polia não se move e a corda desliza sobre ela. Também pre- sumimos que \(m_1 > m_2\). Neste caso, a aceleração é conforme mostrada na Figura. (a) Qual a aceleração do sistema? (b) Qual a tensão na corda?

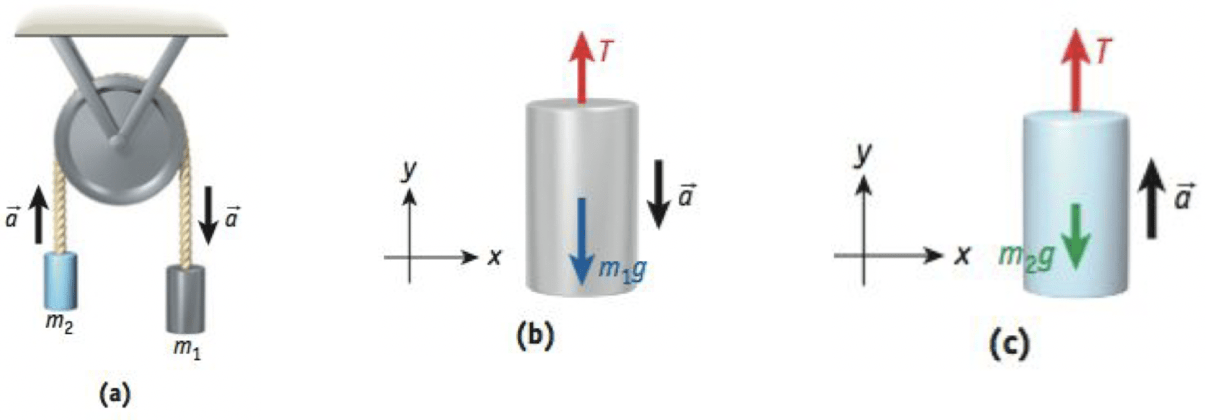
Fonte: Wolfgang

Exemplo 7

Um elevador tem massa de 358,1 kg, e a massa combinada das pessoas dentro dele é de 169,2 kg. O elevador é puxado para cima por um cabo, com aceleração constante de 4,11 m/s\(^2\). Qual é a tensão no cabo?

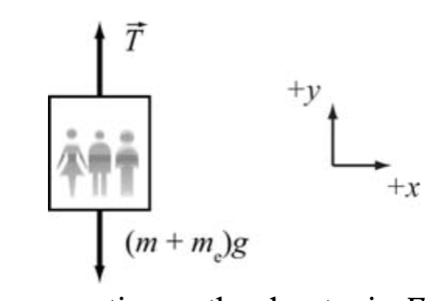
Fonte: Wolfgang

Exemplo 8

O trator de bagagem A mostrado na fotografia tem massa de 450 kg e reboca a carreta B de 275 kg e a carreta C de 160 kg. Por um curto período de tempo, a força de atrito motora desenvolvida nas rodas do trator é de \(F_A\) = (200t) N, onde t é dado em segundos. (a) Se o trator parte do repouso, determine sua velocidade escalar em 2 segundos. (b) Além disso, qual é a força horizontal atuando sobre o engate entre o trator e a carreta B nesse instante? Despreze a dimensão do trator e das carretas.

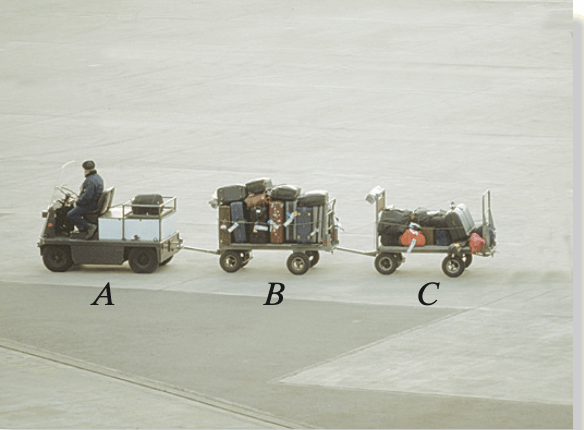
Fonte: Hibbeler

Exemplo 9

O bloco A de 100 kg mostrado na Figura  é solto do repou- so. Se as massas das polias e da corda são desprezadas, determine a velocidade escalar do bloco B de 20 kg em 2 s.  

Fonte: Hibbeler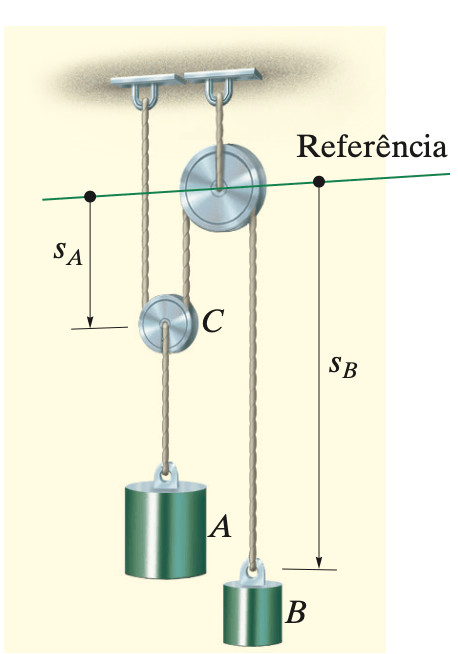

Exemplo 10

Um projétil de 10 kg é disparado para cima verticalmente a partir do solo com uma velocidade inicial de 50 m/s. Determine a altura máxima que ele atingirá se: (a) a resistência atmosférica for desprezada; e (b) a resistência atmosférica for medida como \(F_D\) = (0,01v\(^2\)) N, onde v é a velocidade escalar do projétil a qualquer instante, medida em m/s.  

Fonte: Hibbeler
Fonte: Openstax.org

As leis de Newton

A partir da experimentação

Caso queira ver isso com maiores detalhes

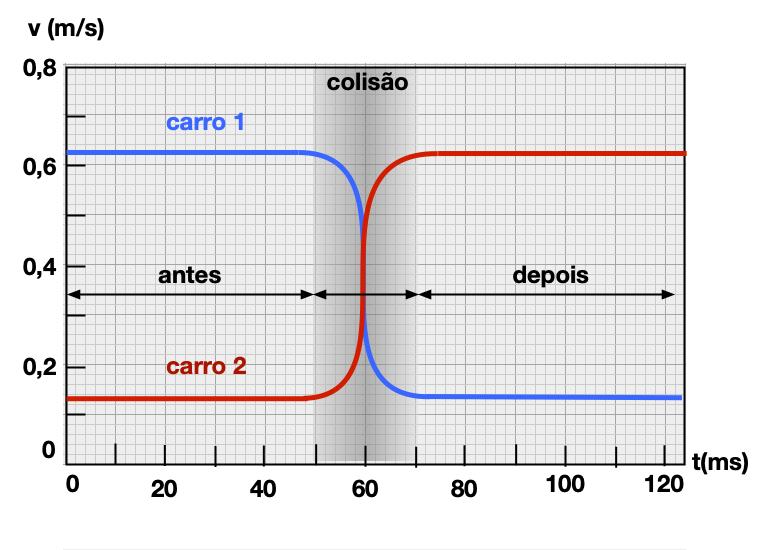
A partir da colisão entre dos carros padrões é possível construir o gráfico da posição versus o tempo.

Aqui temos uma simulação (idealizada) do que ocorre nos laboratórios de física.

As Leis de Newton

Para dois carros idênticos (padrões) há uma troca de velocidades devido a colisão.

\vec v_2 = \vec 0
\vec v_1
\vec v'_1
\vec v'_2
\vec v_2
\vec v_1 = \vec 0
v_1=+0,60\text{ m/s}
v_2=0\text{ m/s}
v_2=+0,60\text{ m/s}
v_1=0\text{ m/s}

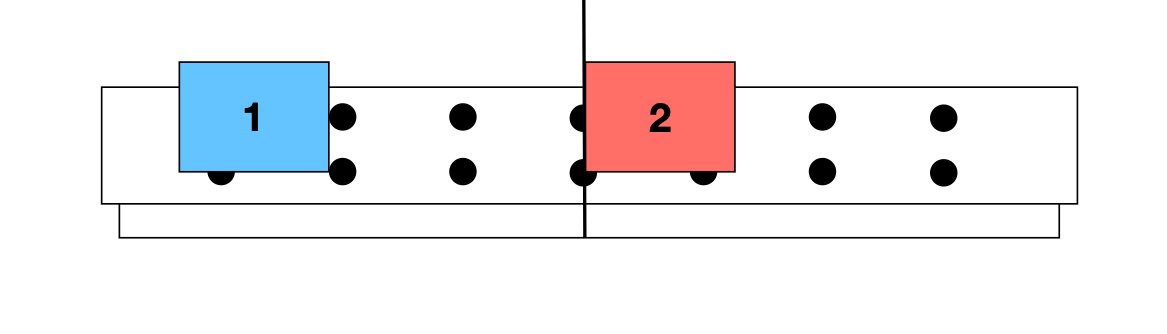
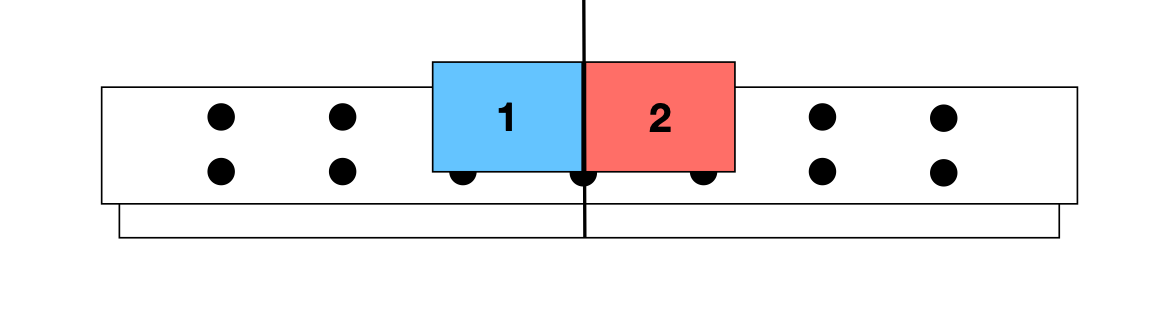
ANTES

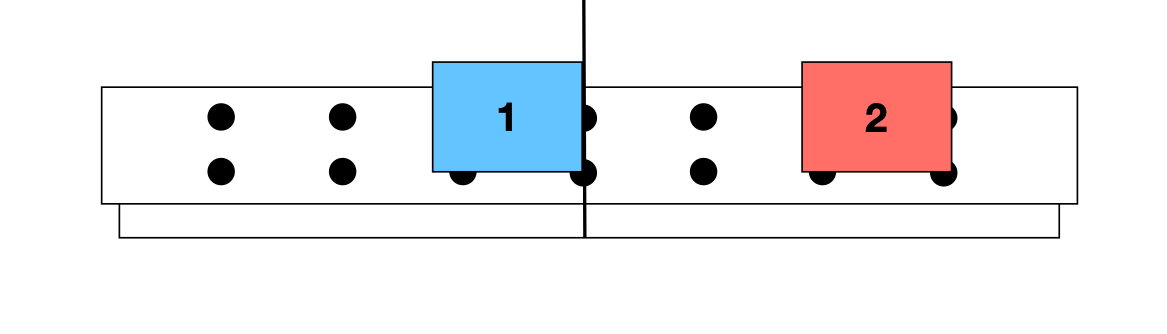
DEPOIS

As Leis de Newton

v_1=+0,62\text{ m/s}
v_2=+0,14\text{ m/s}
v_2=+0,62\text{ m/s}
v_1=+0,14\text{ m/s}

Não importa se um dos carros está em movimento ou em repouso. Há troca de velocidades devido à colisão entre eles.

\vec v_1
\vec v_2
\vec v_1
\vec v_2

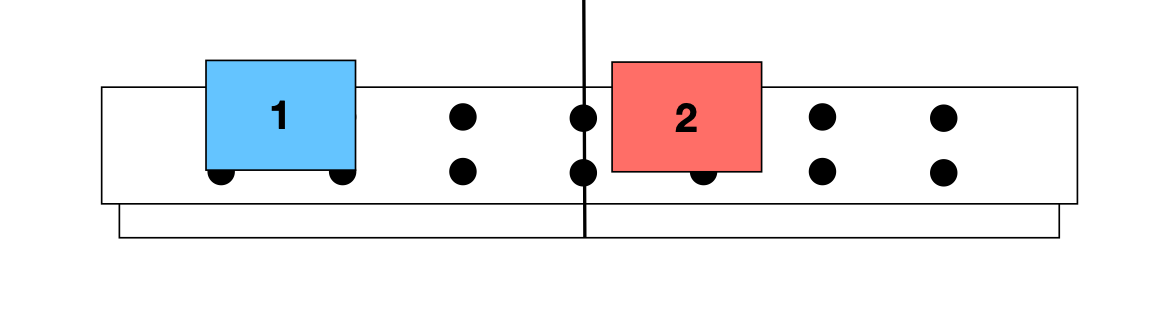
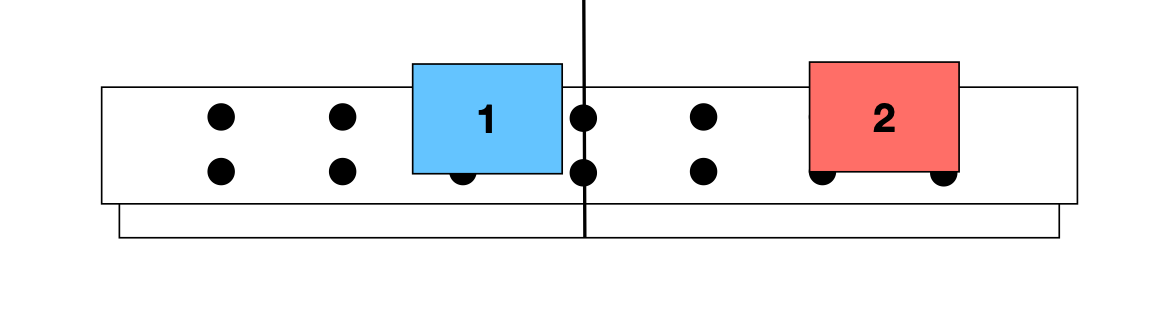
ANTES

DEPOIS

As Leis de Newton

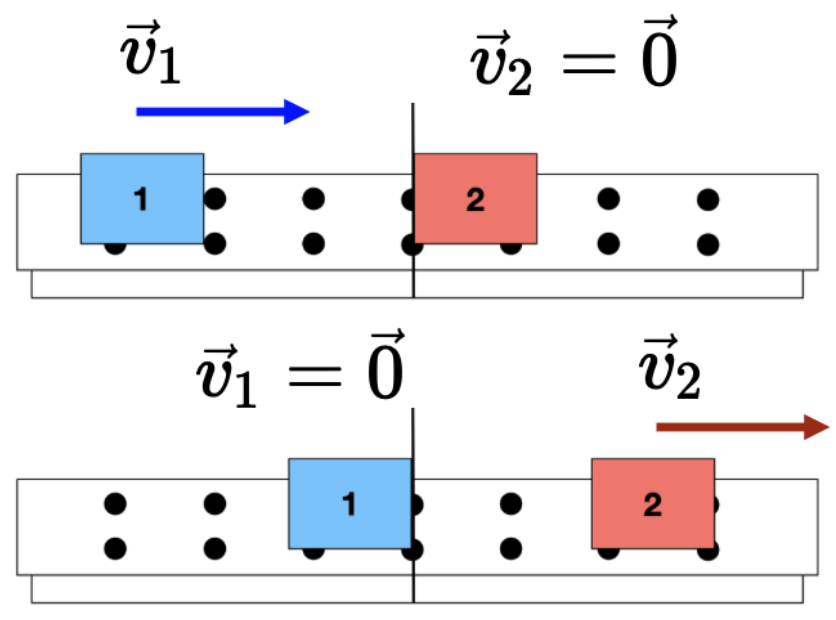
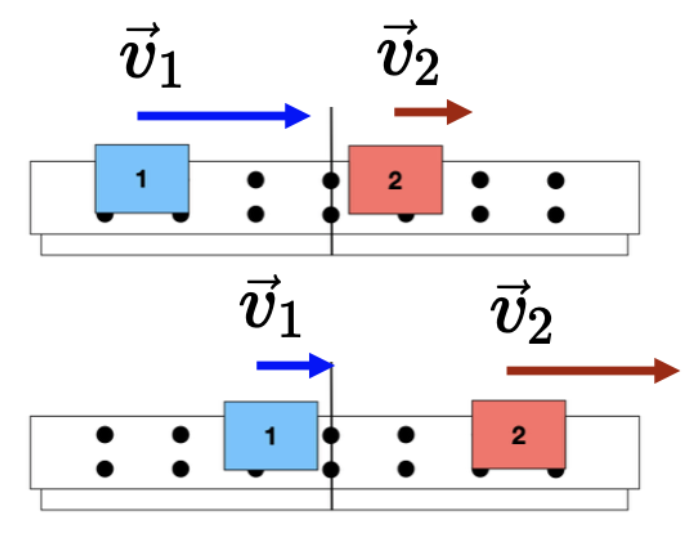
Para dois carros padrões idênticos observamos que:

\Delta \vec v_1 = -\Delta \vec v_2
\Delta v_1=-0,60\text{ m/s}
\Delta v_2=+0,60\text{ m/s}

Caso 1

Caso 2

\Delta v_1=-0,38\text{ m/s}
\Delta v_2=+0,38\text{ m/s}
\frac{|\Delta \vec v_2|}{|\Delta \vec v_1|}=1
\Delta \vec v_1
\Delta \vec v_2
\Delta \vec v_1
\Delta \vec v_2

As Leis de Newton

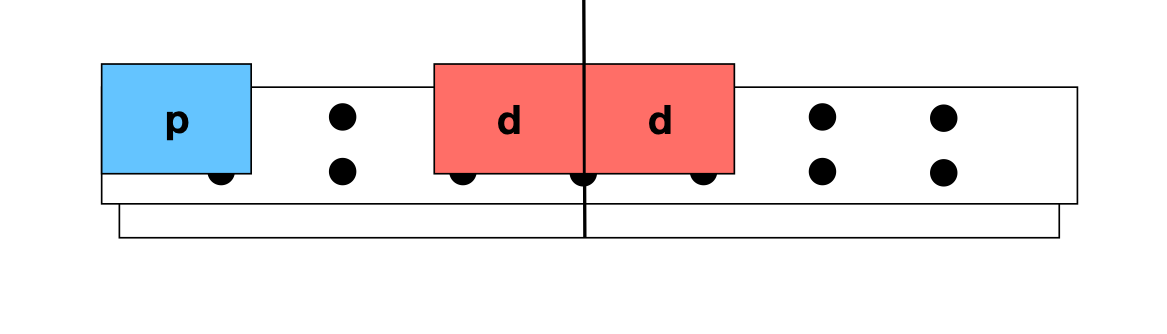
Prendemos dois carros padrões juntos para que o tamanho deste conjunto seja o dobro (d) do tamanho do outro carro padrão (p).

INICIAL

FINAL

v_{p,i} = +0,60\text{ m/s}
v_{d,i} = 0\text{ m/s}
v_{p,f} = -0,20\text{ m/s}
v_{d,f} = +0,40\text{ m/s}

FINAL

INICIAL

\vec v_p
\vec v_d = \vec 0
\vec v_p
\vec v_d
\Delta v_p = -0,80\text{ m/s}
​final - inicial
\Delta v_d = +0,40\text{ m/s}
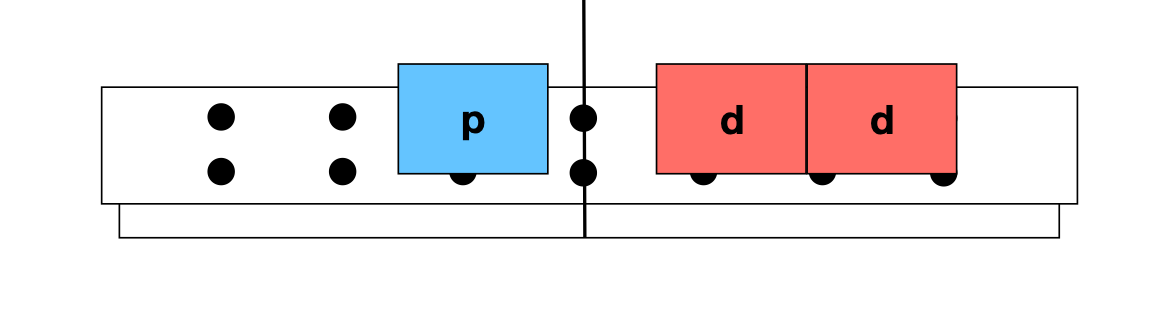
​final - inicial

O que significa esse sinal negativo?

O que significa esse sinal negativo?

As Leis de Newton

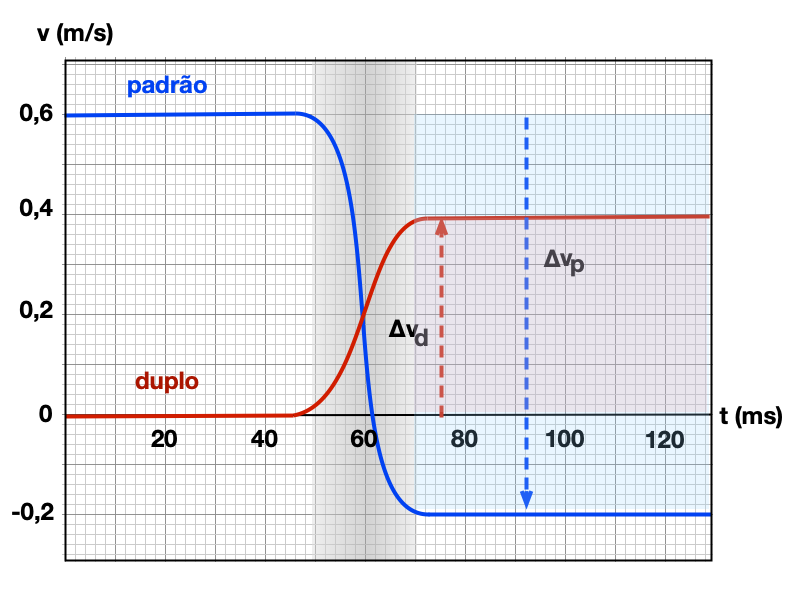
Não importa como os carros se movam (ou não se movam) inicialmente, a variação de velocidade do carro duplo é diferente da variação da velocidade do carro padrão.

\vec v_p
\vec v_d = \vec 0
\vec v_p
\vec v_d
\frac{|\Delta v_d|}{|\Delta v_p|}=\frac{1}{2}

A variação de velocidade do carro padrão é negativa.

A variação da velocidade do carro duplo é positiva.

\Delta v_p = -0,80\text{ m/s}
\Delta v_d = +0,40\text{ m/s}

Para o carro duplo a magnitude da variação da velocidade é a metade da magnitude da variação da velocidade do carro padrão.

\Delta \vec v_p \neq \Delta \vec v_d
\Delta \vec v_p
\Delta \vec v_d

As Leis de Newton

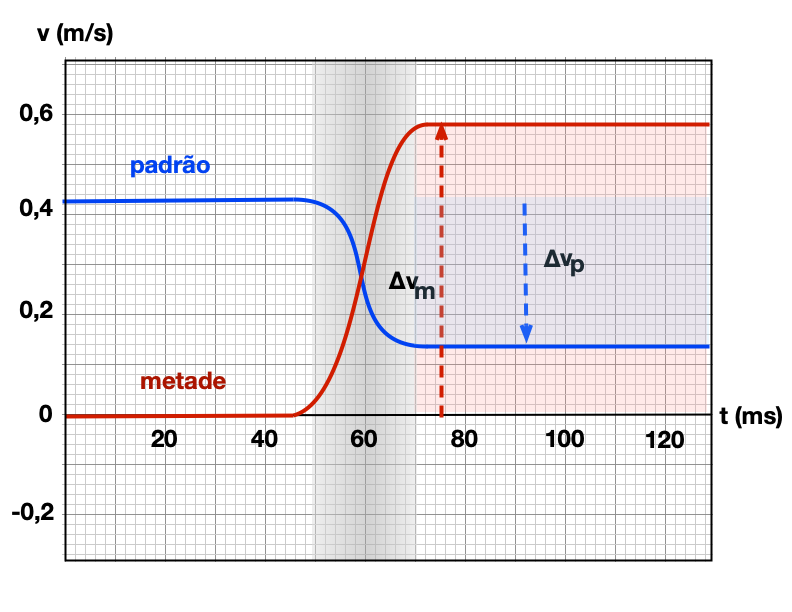
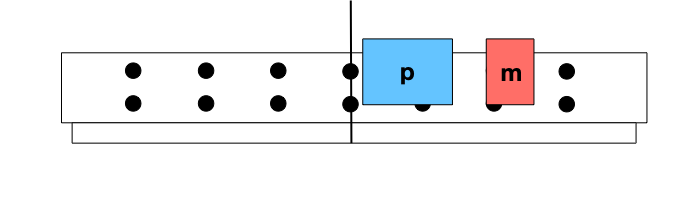
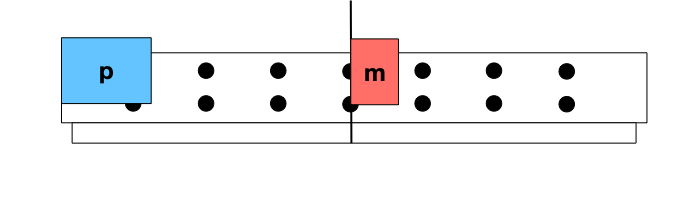
Cortamos um carro padrão ao meio para que o tamanho desta unidade seja a metade (m) do tamanho do outro carro padrão (p).

INICIAL

FINAL

v_p = +0,43\text{ m/s}
v_m = 0\text{ m/s}
v_p =+ 0,14\text{ m/s}
v_m = +0,58\text{ m/s}

FINAL

INICIAL

\Delta v_p = -0,29\text{ m/s}
​final - inicial
\Delta v_m = +0,58\text{ m/s}
​final - inicial
\vec v_p
\vec v_m
\vec v_p
\vec v_m = \vec 0

As Leis de Newton

Não importa como os carros se movam (ou não se movam) inicialmente, a variação da velocidade do meio-carro é diferente da variação da velocidade do carro padrão.

\frac{|\Delta v_m|}{|\Delta v_p|}=2

A variação da velocidade do carro padrão é negativa.

A variação de velocidade do meio-carro é positiva.

\Delta v_p = -0,28\text{ m/s}
\Delta v_m = +0,58\text{ m/s}

Para o meio-carro a magnitude da variação da velocidade é o dobro da magnitude da variação da velocidade do carro padrão.

\vec v_p
\vec v_m
\vec v_p
\vec v_m = \vec 0
\Delta \vec v_p \neq \Delta \vec v_m
\Delta \vec v_p
\Delta \vec v_m

As Leis de Newton

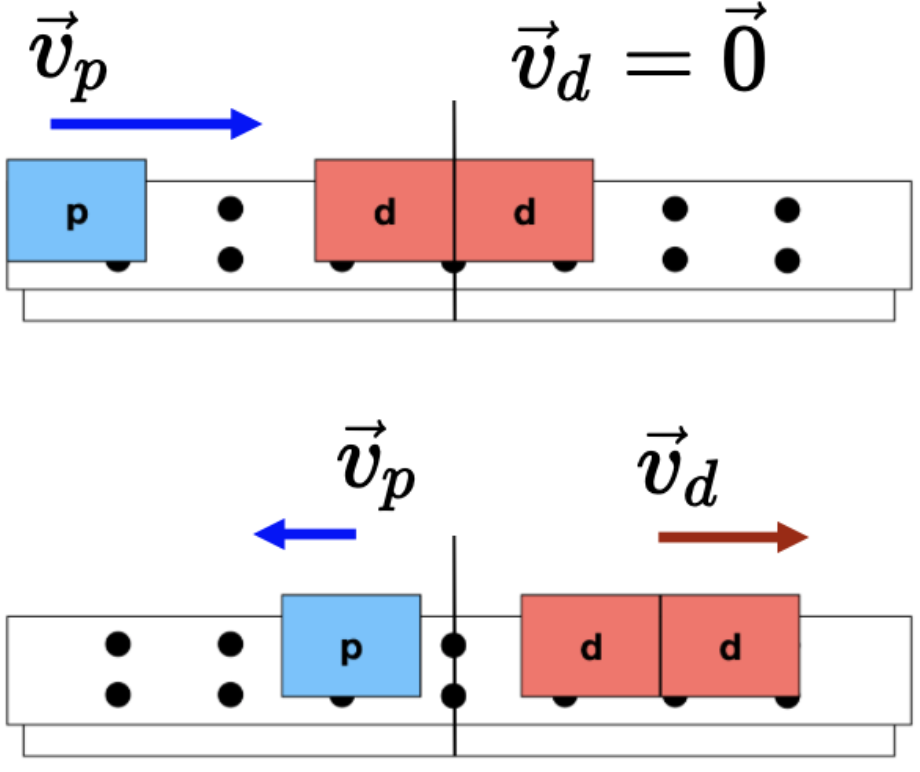
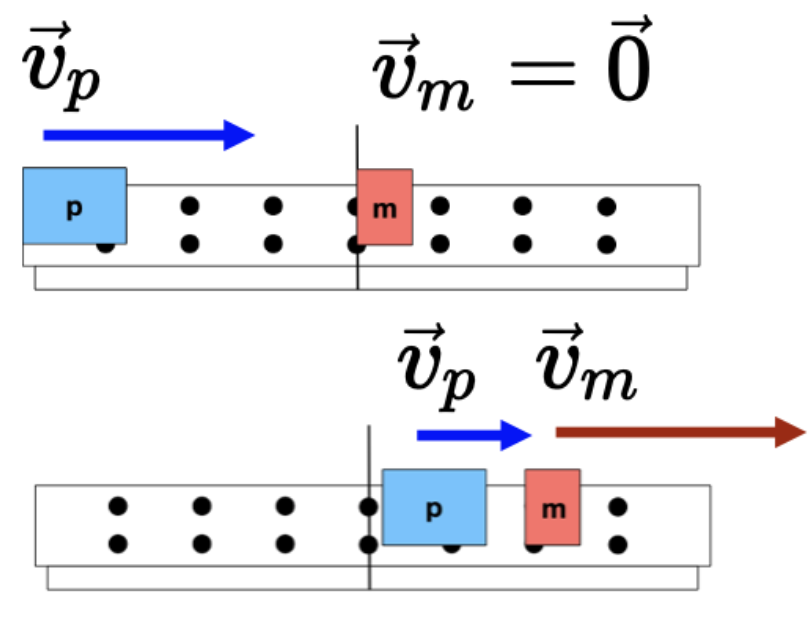
Para dois carros padrões que não são idênticos observamos que:

\Delta \vec v_1 \neq\Delta \vec v_2

Caso 3

Caso 4

\frac{|\Delta \vec v_d|}{|\Delta \vec v_p|}=\frac{1}{2}
\Delta \vec v_p
\Delta \vec v_d
\Delta \vec v_p
\Delta \vec v_m
\Delta v_p = -0,80\text{ m/s}
\Delta v_d = +0,40\text{ m/s}
\Delta v_p = -0,28\text{ m/s}
\Delta v_m = +0,58\text{ m/s}
\frac{|\Delta \vec v_m|}{|\Delta \vec v_p|}=2
\Rightarrow
\Leftarrow

As Leis de Newton

A razão das inércias dos dois carros é igual ao inverso da razão de suas variações de velocidade.

m_1 \propto \frac{1}{|\Delta v_1|}
\frac{m_2}{m_1} = \frac{|\Delta v_1|}{|\Delta v_2|}
m_2 \propto \frac{1}{|\Delta v_2|}
\Rightarrow

Se

Experimento Carro 1 Carro 2
1 e 2 padrão padrão 1,0 1,0
3 padrão dobro 2,0 0,5
4 padrão metade 0,5 2,0

Inércia (\(m\))

Razão das inércias

Razão da variação das velocidades

=m_1/m_2
=m_1/m_2
=m_1/m_2
m_2/m_1
|\Delta v_2|/|\Delta v_1|

Verificamos experimentalmente que existe uma relação entre a inércia e a variação das velocidades:

As Leis de Newton

A aceleração média de cada carrinho é:

a_m=\frac{\Delta v}{\Delta t}

E a razão entre as acelerações são proporcionais a uma constante positiva que depende apenas das partículas e não depende do movimento de cada partícula. A razão é proporcional às massas inerciais, mas em uma razão inversa:

\frac{a_{m,1}}{a_{m,2}}=-\frac{m_2}{m_1}

Fonte: https://www.compadre.org/physlets/

Colisões de curto e longo alcance

As Leis de Newton

No movimento forçado a interação da partícula A com a partícula B se manifesta pelo fato do corpo sair do Movimento Retilíneo Uniforme.

m_1a_1=-m_2a_2
F_{12}=-F_{21}

As forças sempre vêm aos pares (reciprocidade da força):

Quando dois objetos interagem, cada um exerce uma força sobre o outro.

m_1=0,12\text{ kg}
m_2=0,24\text{ kg}
v_{12}=0,60\text{ m/s}

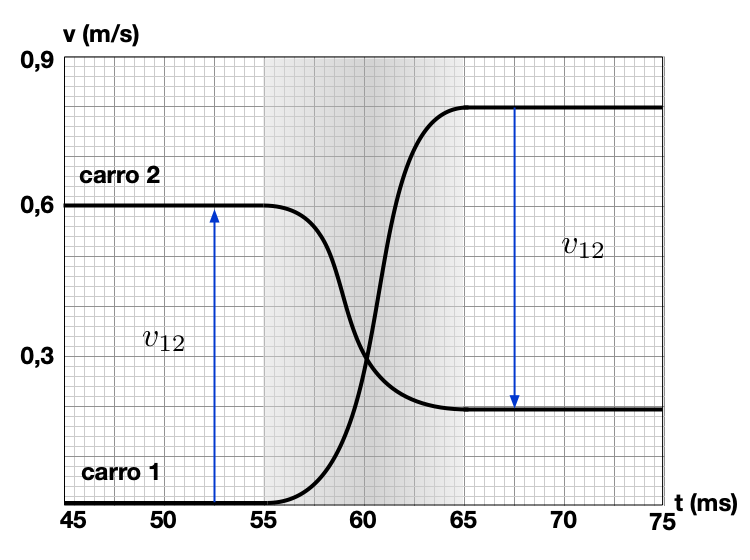
A única diferença entre as duas colisões é que a interação é suavizada por uma mola.

v_{12,i}=v_{12,f}
\Delta t = 10\text{ ms}
\Delta t = 1\text{ ms}

sem mola \(\Rightarrow\)

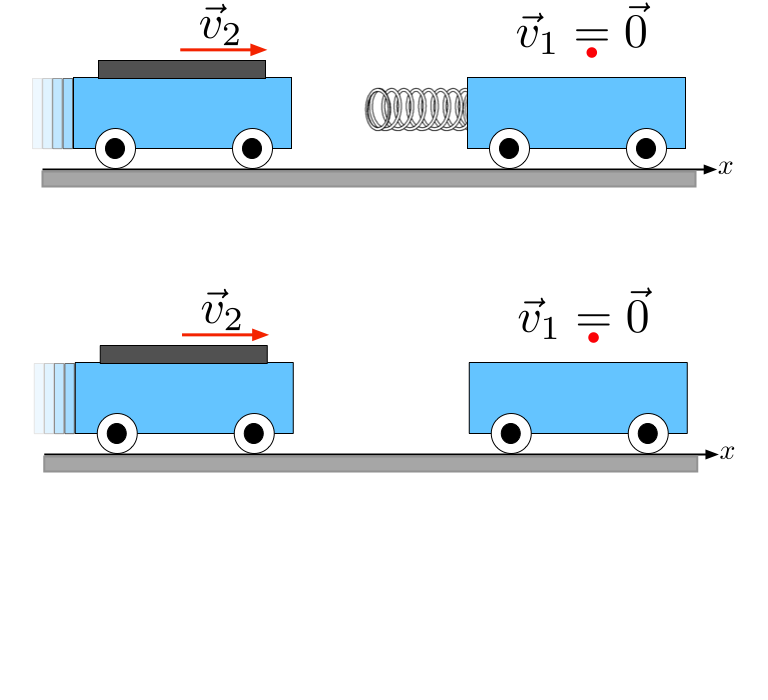
\(\Leftarrow\) com mola

As Leis de Newton

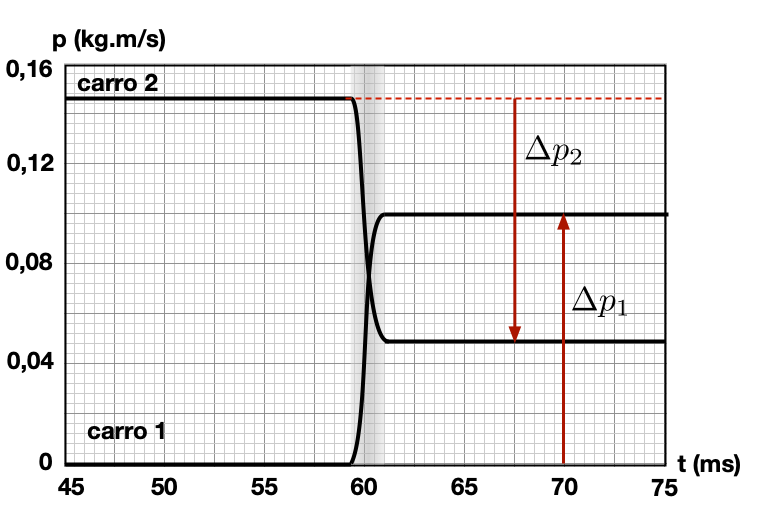
A variação de momento do carrinho 1 é compensada por uma variação no momento do carrinho 2. Vejamos a interação do sistema isolado dos carros com mola.

\Delta p_{1,c/m}=+0,096\text{ kg.m/s}
F_{\text{por 2 em 1}} = \frac{\Delta p_{1,c/m}}{\Delta t}
=\frac{+0,096\text{ kg.m/s}}{0,010\text{ s}}=+9,6\text{ N}
\Delta p_{2,c/m}=-0,096\text{ kg.m/s}
F_{\text{por 1 em 2}} = \frac{\Delta p_{2,c/m}}{\Delta t}
=\frac{-0,096\text{ kg.m/s}}{0,010\text{ s}}=-9,6\text{ N}

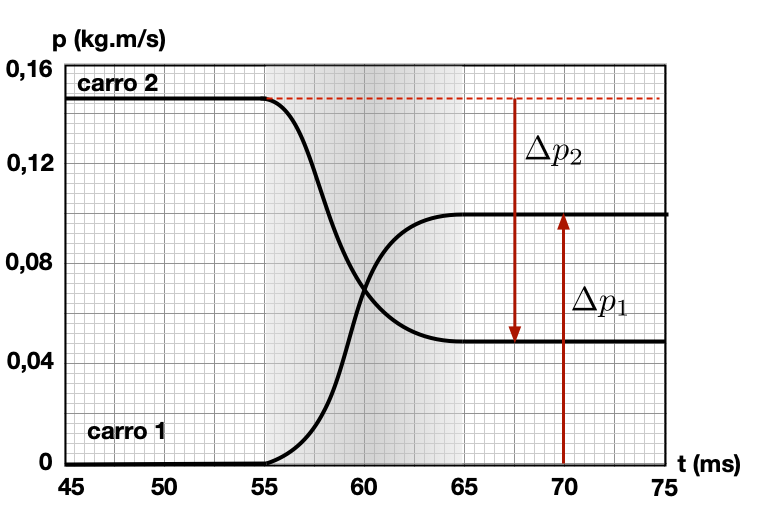
carro 1

carro 2

Sistema Isolado dos carros com mola

\Delta p_{1,c/m}+\Delta p_{2,c/m} = 0
(F_{21}+F_{12})\Delta t=0
F_{21}=-F_{12}
\Rightarrow
\Rightarrow

As Leis de Newton

\Delta t = 10\text{ ms}
I
\vec F_{21}
\vec F_{12}

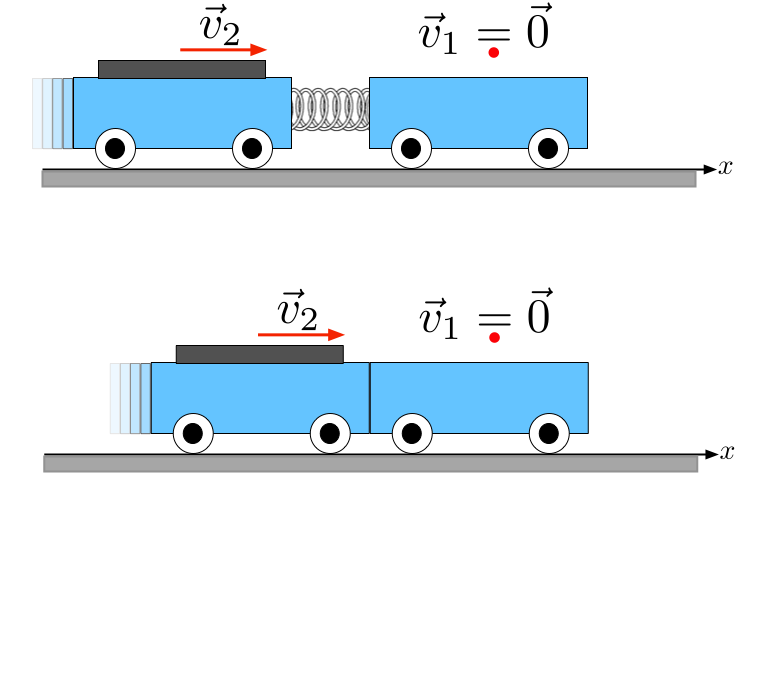
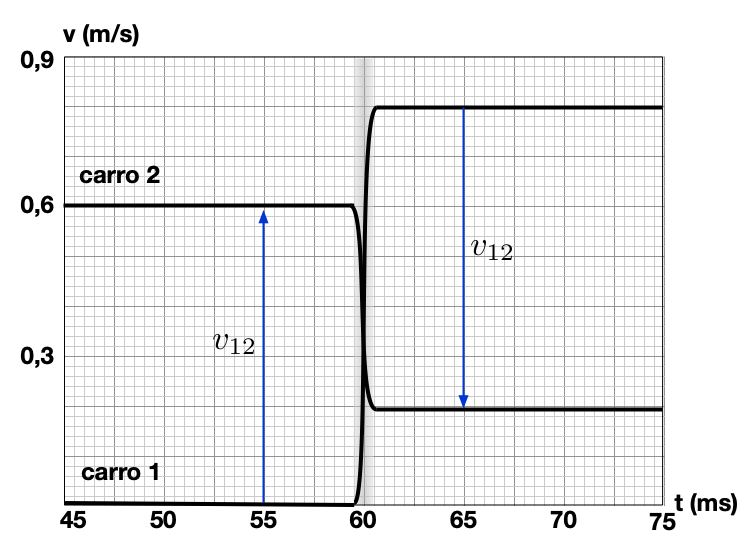
Em ambas as colisões a variação de momento do carrinho 1 é compensada por uma variação no momento do carrinho 2. Vejamos a interação do sistema de carros sem mola.

\Delta p_{1,s/m}=+0,096\text{ kg.m/s}
F_{\text{por 2 em 1}} = \frac{\Delta p_{1,s/m}}{\Delta t}
=\frac{+0,096\text{ kg.m/s}}{0,001\text{ s}}=+96\text{ N}
\Delta p_{2,s/m}=-0,096\text{ kg.m/s}
F_{\text{por 1 em 2}} = \frac{\Delta p_{2,s/m}}{\Delta t}
=\frac{-0,096\text{ kg.m/s}}{0,001\text{ s}}=-96\text{ N}

carro 1

carro 2

Sistema Isolado dos carros sem mola

As Leis de Newton

\Delta t = 1\text{ ms}
\Delta p_{1,s/m}+\Delta p_{2,s/m} = 0
(F_{21}+F_{12})\Delta t=0
F_{21}=-F_{12}
\Rightarrow
\Rightarrow
I
\vec F_{21}
\vec F_{12}
\vec F_{21}=-\vec F_{12}

Sempre que dois objetos interagem, exercem um sobre o outro forças que são iguais em magnitude e direção, mas opostas em sentido.

O par de forças que dois objetos em interação exercem um sobre o outro é chamado par de interação.

As Leis de Newton

A conclusão de que objetos em interação exercem forças iguais na mesma direção, mas em sentidos opostos um sobre o outro é um resultado direto da lei da conservação do momento e da nossa definição de força.

\Delta \vec p_{1}+\Delta\vec p_{2} = 0
(\vec F_{21}+\vec F_{12})\Delta t=0
\Rightarrow
\Rightarrow
\vec F_{21}=-\vec F_{12}
não há força externa resultante!
há força internas que são um par de interação!
\vec F_{12}
\vec F_{21}
Made with Slides.com