
Lección 3: Modelado de sistemas mecánicos lineales
IE3036 - Sistemas de Control 1
2do ciclo, 2024
¿Por qué?
Sistemas de parámetro concentrado
Elementos (lineales) básicos
+
Leyes fundamentales
Ejemplo: circuitos eléctricos

Ejemplo: circuitos eléctricos

Leyes de Kirchhoff
Sistemas mecánicos traslacionales

Segunda Ley de Newton
¿Cuál es el modelo del sistema?
impedancia mecánica \(Z_M\)

El método de impedancias
Válido para \(N\) masas, aunque se presenta \(N=2\) como ejemplo
Aplique el método de impedancias
1/4 de la masa del automóvil

suspensión
rueda
llanta
superficie del camino
modelo de 1/4 de carro
Ejemplo de aplicación
>> clase3_suspension.m
>> clase3_suspension.m
¿Qué ocurrió con la gravedad?
Ejercicio 1
Aplique el método de impedancias
Sistemas mecánicos rotacionales


Segunda Ley de Newton (rotacional)
cojinete
torsión
misma estructura que el problema de suspensión
Sistemas con engranajes
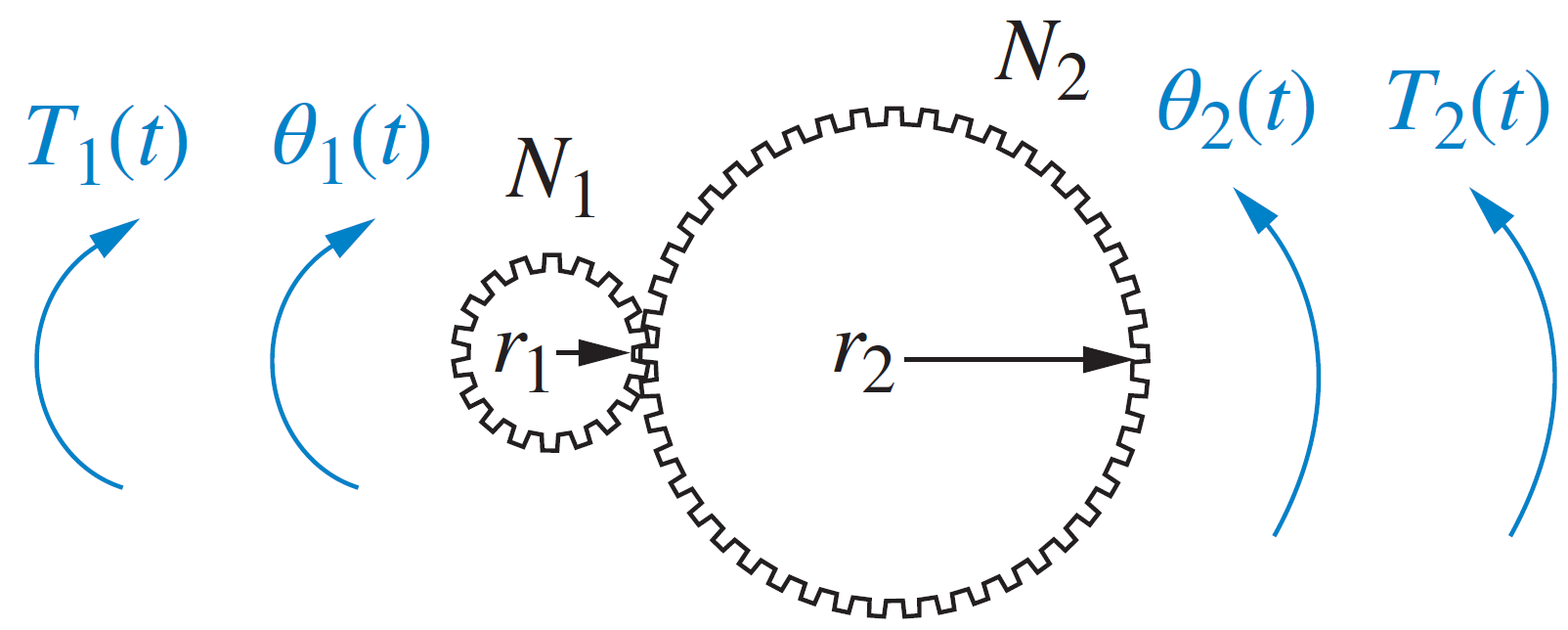
Sistemas con engranajes

Asumiendo engranajes estándar, lubricados y sin backlash.
Elimine la reducción de engranajes
motor
potencia
carga
Reflejo de impedancias
por lo general buscando llevar las impedancias de la carga a la potencia
Sistemas mixtos
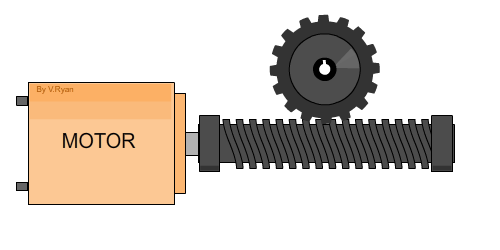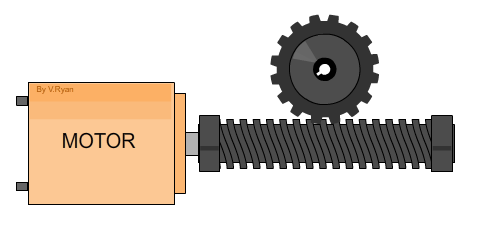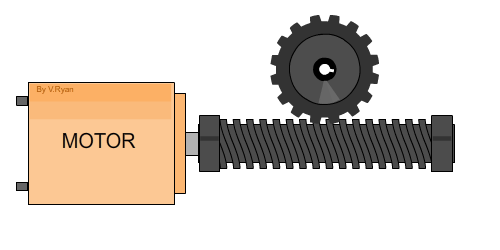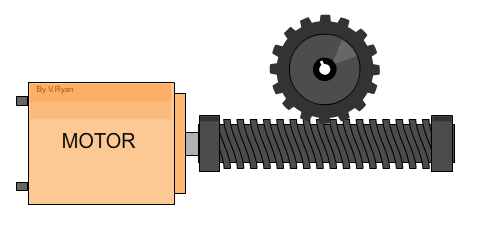
Ejercicio 2
Aplique el método de impedancias