Lección 2: Funciones de Transferencia y Diagramas de Bloques

IE3036 - Sistemas de Control 1
2do ciclo, 2024
¿Por qué?
planta
entrada
salida
función de transferencia
Ejemplo: ¿Cuál es la respuesta en el tiempo del sistema si la entrada es el escalón unitario?
Ejemplo: ¿Cuál es la respuesta en el tiempo del sistema si la entrada es el escalón unitario?
Ejemplo: ¿Cuál es la respuesta impulsional del sistema?
Ejemplo: ¿Cuál es la respuesta impulsional del sistema?
Análisis en Matlab
G = tf(10, [1, -4, -12])
step(G);
impulse(G);
linearSystemAnalyzer(G);ejemplo_analisis.m
Ejemplo: Encuentre la EDO que describe al sistema LTI con función de transferencia:
Ejemplo: Encuentre la EDO que describe al sistema LTI con función de transferencia.
Ejercicio 1
Encuentre la respuesta en el tiempo del sistema
Ejercicio 1
G = tf([3, 12, 11], [1, 5, 6]);
t = 0:0.01:5;
u = exp(-t);
lsim(G, u, t);
Tratemos de obtener intuición sobre \(G(s)\)

distancia recorrida 1D
resistencia del viento
fuerza de empuje ("gas")
cosa
otra cosa
Interconexión de múltiples sistemas
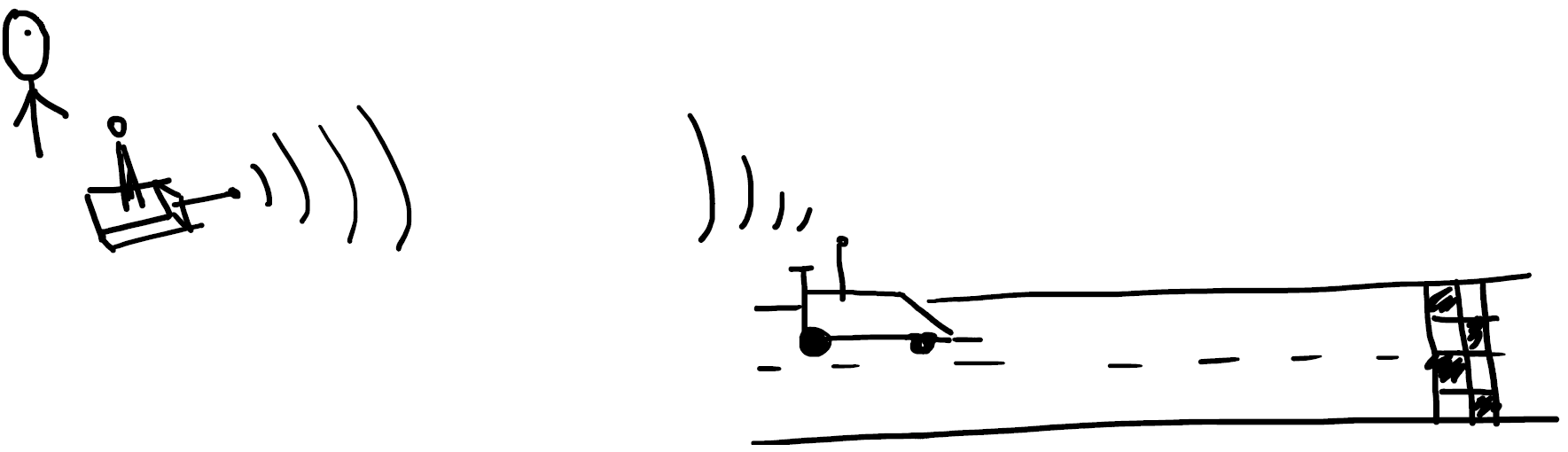
mano
joystick
sensor
emisor
(medio)
receptor
carro
referencia
joystick
emisor
medio
receptor
carro
Diagramas de bloques
Ejemplo: servomotor
referencia
motor
sensor
controlador
salida
driver

\(\big\uparrow\) intuición
\(\big\downarrow\) facilidad algebráica
¿Cómo retomamos la facilidad algebraica?
Álgebra de bloques
Los diagramas de bloques nos indican cómo interconectar los elementos en los sistemas...
Reglas fundamentales
Conexión en serie | cascada
Geq = G1 * G2Conexión en paralelo
Geq = G1 + G2Retroalimentación negativa
Geq = feedback(G1, G2)¿Puede demostrarlo?
Ejemplo: Encuentre el equivalente en lazo abierto del siguiente diagrama de bloques.
Simplificación y análisis en Matlab (Control Systems Toolbox)
ejemplo_bloques.m
Regresando al lazo de control canónico
lazo cerrado | implementación
lazo cerrado | implementación
\(E(s)\)
error
\(U(s)\)
controlador
planta
sensor
lazo abierto| análisis
Ejercicio 2