IE3036 - Sistemas de Control 1
2do ciclo, 2024
Lección 13: Sistemas de datos muestreados
Sistemas de control y la revolución digital
¿Qué podemos digitalizar?
¿Qué podemos digitalizar?
\(\mu\)C
¿Qué podemos digitalizar?
\(\mu\)C
sensor digital
¿Qué podemos digitalizar?
\(\mu\)C
sensor digital
software
¿Qué podemos digitalizar?
\(\mu\)C
sensor digital
software
Imposible reemplazar la planta por un equivalente digital.
Dos topologías para resolver este problema
ADC
ref.
control
DAC
planta
sensor
salida
Topología 1: sólo se digitaliza el control
ADC
ref.
control
DAC
planta
sensor
salida
Topología 1: sólo se digitaliza el control
microcontrolador | computadora
ADC
ref.
control
DAC
planta
sensor
salida
Topología 1: sólo se digitaliza el control
microcontrolador | computadora
Diseño indirecto de controladores digitales.
Topología 2: sólo la planta no se digitaliza
control
ref.
DAC
planta
sensor
salida
ADC
Topología 2: sólo la planta no se digitaliza
microcontrolador | computadora
control
ref.
DAC
planta
sensor
salida
ADC
Topología 2: sólo la planta no se digitaliza
microcontrolador | computadora
control
ref.
DAC
planta
sensor
salida
ADC
sensor digital
Topología 2: sólo la planta no se digitaliza
microcontrolador | computadora
Diseño directo de controladores digitales.
control
ref.
DAC
planta
sensor
salida
ADC
sensor digital
sólo esta queda continua
microcontrolador | computadora
diseño directo de controladores digitales
control
ref.
DAC
planta
sensor
salida
ADC
sensor digital
sólo esta queda continua
Sin importar la topología, no nos escapamos de tener que hacer un análisis mezclado: digital + analógico = sistemas de datos muestreados.
microcontrolador | computadora
diseño directo de controladores digitales
control
ref.
DAC
planta
sensor
salida
ADC
sensor digital
sólo esta queda continua
Sin importar la topología, no nos escapamos de tener que hacer un análisis mezclado: digital + analógico = sistemas de datos muestreados.
¿Cómo se logra? Matematizando al ADC y al DAC.
Matematizando al ADC
muestreo
muestreo
+ cuantificación
muestreo
+ cuantificación
muestreo
+ cuantificación
Si ambas cuadrículas son finas entonces
digital \(\approx\) analógica.
muestreo
+ cuantificación
compleja de modelar por su naturaleza estocástica
Muestreo ideal de señales continuas
Muestreo ideal de señales continuas
Muestreo ideal de señales continuas
Muestreo ideal de señales continuas
Versión "digitalizada" de \(u(t)\)
esta es una señal discreta
esta es una señal discreta
Esto se ve considerablemente complicado en el tiempo...
esta es una señal discreta
Esto se ve considerablemente complicado en el tiempo...
¿Cómo se verá en Laplace?
Esta es la transformada \(\mathcal{Z}\) de la señal discreta \(u(kT)\).
cuando \(z=e^{sT}\)
Función de transferencia del sistema discreto.
Función de transferencia del sistema discreto.
Aplica toda la teoría de procesamiento digital de señales.
Función de transferencia del sistema discreto.
Aplica toda la teoría de procesamiento digital de señales*.
* cuidado en las tablas por el cambio
\(n\to kT\)
Ejemplo
¿Cuál es la transformada \(\mathcal{Z}\) de \(u(t)=\sin(\omega_0 t)\) luego de ser muestreada con período \(T\)?
Ejemplo
¿Cuál es la transformada \(\mathcal{Z}\) de \(u(t)=\sin(\omega_0 t)\) luego de ser muestreada con período \(T\)?
Ejemplo
¿Cuál es la salida \(y^\star(t)\) del sistema discreto con función de transferencia \(G(z)=\frac{1}{1-0.5z^{-1}}\), si la entrada es \(u(t)=\mathbf{1}(t)\) luego de ser muestreada con período \(T\)?
Ejemplo
¿Cuál es la salida \(y^\star(t)\) del sistema discreto con función de transferencia \(G(z)=\frac{1}{1-0.5z^{-1}}\), si la entrada es \(u(t)=\mathbf{1}(t)\) luego de ser muestreada con período \(T\)?
En conclusión
ADC
Muestreador (sampler)
Matematizando al DAC
¿Cómo recuperamos a \(u(t)\)? \(\Rightarrow\) Interpolación
El zero-order hold
ZOH
El zero-order hold
ZOH
Pérdida de información inherente a la digitalización.
delay
En conclusión
DAC
zero-order hold (ZOH)
Regresando a las dos topologías de control digital
Topología 1: diseño indirecto
Topología 1: diseño indirecto
Topología 1: diseño indirecto
señal de tiempo continuo
señal de tiempo continuo
Topología 1: diseño indirecto
señal de tiempo continuo
sistema de tiempo continuo
señal de tiempo continuo
Topología 1: diseño indirecto
señal de tiempo continuo
sistema de tiempo continuo
señal de tiempo continuo
Diseño por emulación discreta de controladores analógicos.
Topología 2: diseño directo
Topología 2: diseño directo
muestreador ficticio
Topología 2: diseño directo
Topología 2: diseño directo
señal de tiempo discreto
señal de tiempo discreto
Topología 2: diseño directo
señal de tiempo discreto
señal de tiempo discreto
sistema de tiempo discreto
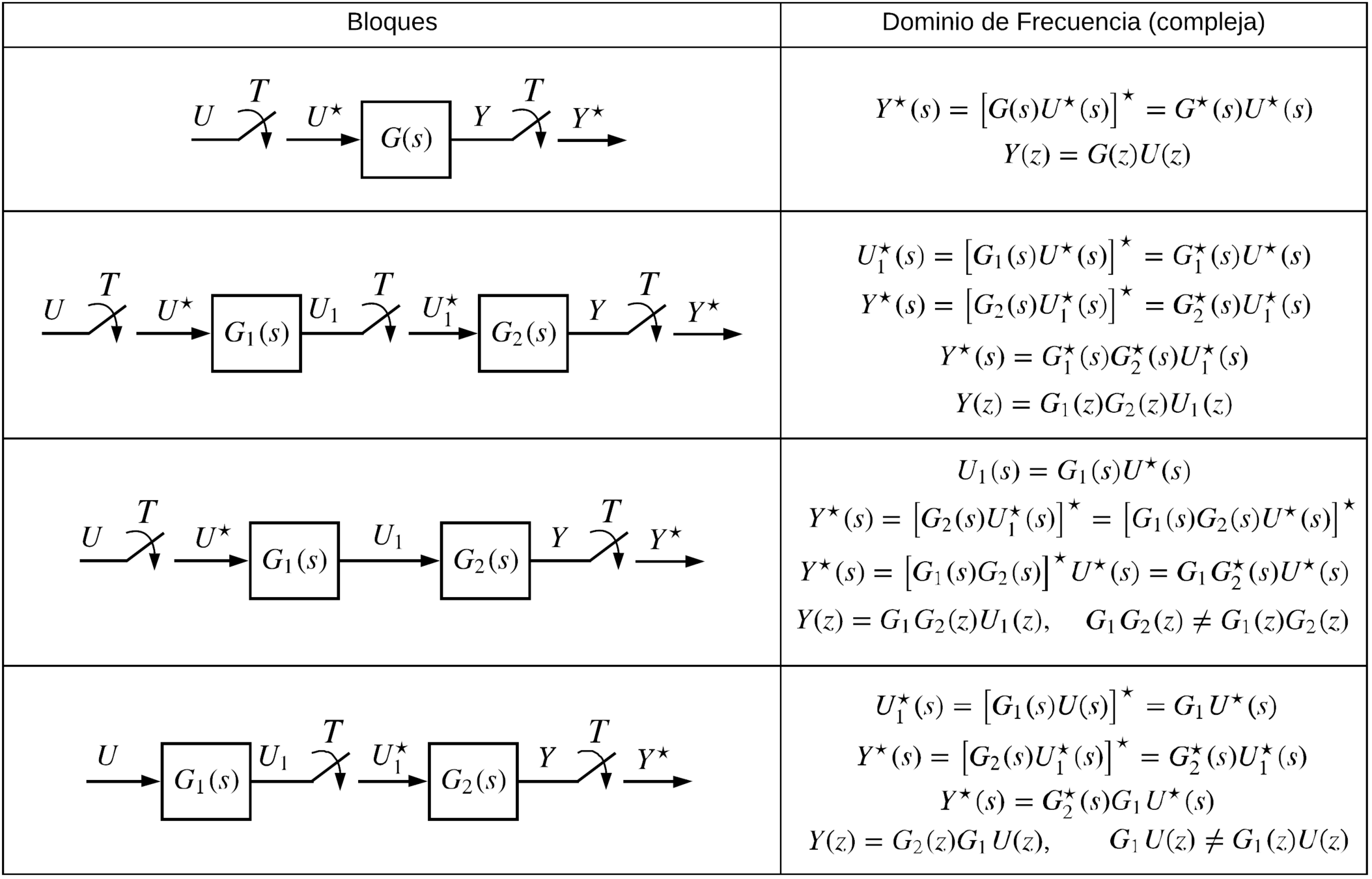
Álgebra de bloques con muestreadores