Julien B.
Group Meeting, October 11th 2024
Zoology of Honeycomb Floquet codes
Depths & Logical operations
Ideas leading to the Floquet codes
Stabilizer codes
\text {For a stabilizer code }\llbracket n,k,d \rrbracket
\forall s \in \mathcal{S},s\bar{\ket{\psi}} = {\color{red}+} \bar{\ket{\psi}}
k = n-rank(\mathcal{S})
\set{\forall s_i,s_j \in \mathcal{S} \subsetneq\mathcal{P}^n,[s_i,s_j]=0}
The toric code

Subsystem codes
\text {For a subsystem code }\llbracket n,k,d \rrbracket
\text{Add checks s.t. }[c,\mathcal{S}]=0
\forall s \in \mathcal{S},\exists I,\prod_{i\in I}c_i = s
Kitaev inspired version
Kitaev model
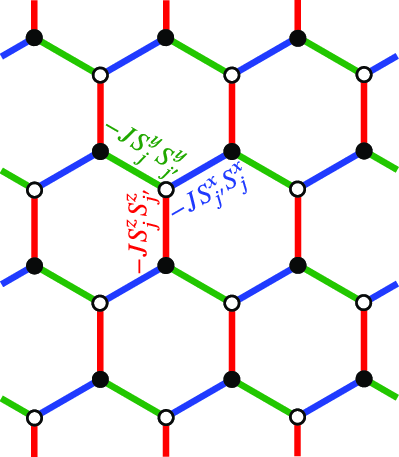
With a bunch of local unitaries

Any tricolored lattice

Process


'Free' gates

'Free' gates

'Free' gates

'Free' gates

Equivalent codes


Colour code inspired version
Colour code

CSS code



Decoding comparison

Going Planar
Going Planar
- Surface code approach
- Colour code approach
Surface code

Gidney & Newman


Kesselring & Magdalena de la F.
Colour code

Kesselring & Magdalena de la F.
'Exotic idea' code
Vuillot

