Long-Range Correlations and Cat States
in a Many-Body Localized Regime





Anderson insulator
disorder \(h \)
Interaction \(\Delta\)
Ergodic
Many-body localized (?)
Jeanne Colbois | Institut Néel | QuantAlps days 2025
?

Nicolas Laflorencie

Ashirbad Padhan

Fabien Alet
1
Anderson localization in 1D
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
Conserves \(N_f\)
1
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
Conserves \(N_f\)
1
\(|\psi(x)|^2\)
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
\(|\psi(x)|^2\)
Conserves \(N_f\)
1
\(h\)
\(-h\)
\(h\)
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Conserves \(N_f\)
1
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Conserves \(N_f\)
1
- Absence of diffusion
- Absence of transport
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Conserves \(N_f\)
1
- Absence of diffusion
- Absence of transport
Anderson insulator
disorder \(h \)
2
What happens For many, interacting fermions ?
Anderson insulator
disorder \(h \)
Interaction \(\Delta\)
2
What happens For many, interacting fermions ?
Anderson insulator
disorder \(h \)
Interaction \(\Delta\)
Is the many-body wavefunction still "localized"?
Absence of transport
Absence of thermalization
in some isolated quantum-many body systems
3
Fermions and spins
\(-h\)
\(h\)
3
Fermions and spins
\(-h\)
\(h\)
Attraction / repulsion
3
Fermions and spins
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
\(n_i = S_i^z + 1/2\)
3
Fermions and spins
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
\(n_i = S_i^z + 1/2\)
Spin-flip
3
Fermions and spins
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
\(n_i = S_i^z + 1/2\)
ISING INTERACTION
Spin-flip
3
Fermions and spins
\(-h\)
\(h\)
Attraction / repulsion
ISING INTERACTION
Spin-flip
Jordan-Wigner
non-local transformation
\(n_i = S_i^z + 1/2\)
3
Fermions and spins
\(-h\)
\(h\)
Attraction / repulsion
\(n_i = S_i^z + 1/2\)
ISING INTERACTION
Spin-flip
\(L/2\) fermions
Charge is conserved
\(\sum_i S_i^{z} = 0\)
Magnetization is conserved
Jordan-Wigner
non-local transformation
Scope
4
1. From Anderson to many-body localization
2. Instabilities of many-body localization
On a spin chain:
3. Strong, long-range correlations deep in the MBL regime
From Anderson to many-body localization
1. From one to many fermions
2. Adding interactions
many non-interacting Fermions
Conserves \(N_f\)
5
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
many non-interacting Fermions
Conserves \(N_f\)
Slater determinant based on localized wavefunctions
5
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
many non-interacting Fermions
Conserves \(N_f\)
\(\xi(h, E)\)










Slater determinant based on localized wavefunctions
5
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
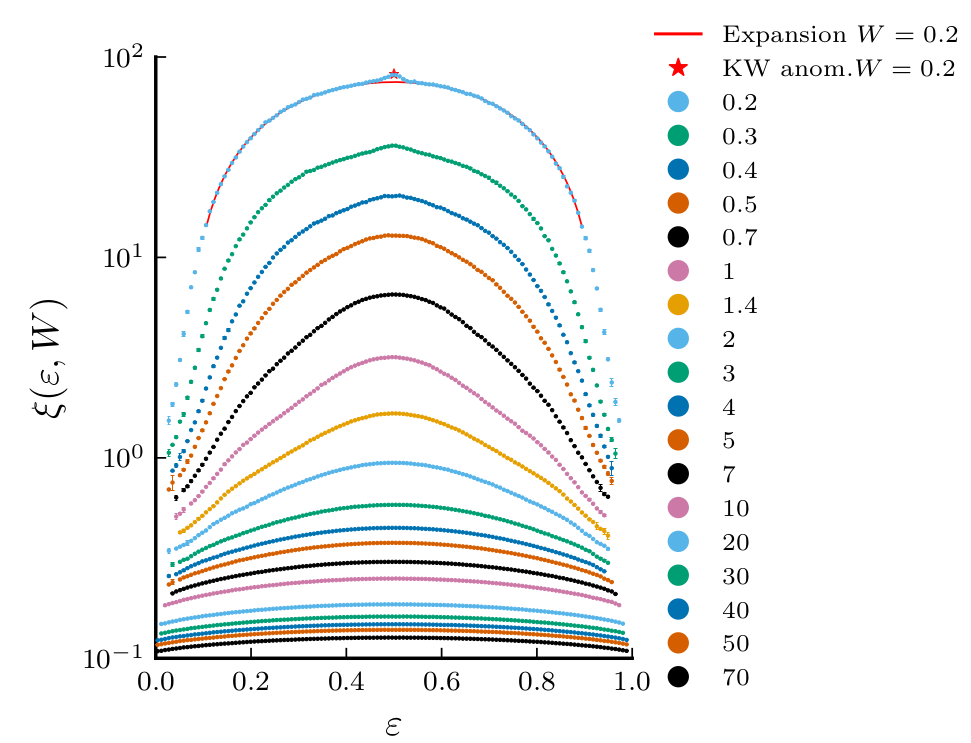
\(\epsilon\)
\(\xi(\epsilon, W)\)










Many-body Anderson lOCALIZATION Length?
6
Colbois and Laflorencie (2023)
See also Müller & Delande review

\(\epsilon\)
\(\xi(\epsilon, W)\)










Many-body Anderson lOCALIZATION Length?
6
Colbois and Laflorencie (2023)
See also Müller & Delande review

\(\epsilon\)
\(\xi(\epsilon, W)\)
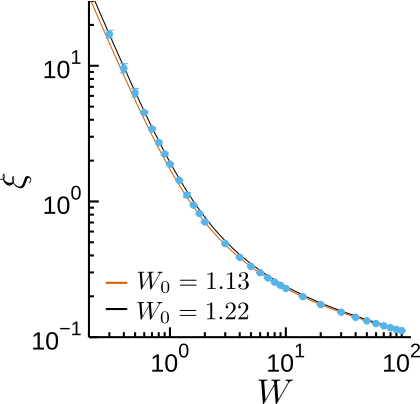










Many-body Anderson lOCALIZATION Length?
6
Colbois and Laflorencie (2023)
See also Müller & Delande review
\(h\)

\(\epsilon\)
\(\xi(\epsilon, W)\)











Many-body Anderson lOCALIZATION Length?
6
Colbois and Laflorencie (2023)
See also Müller & Delande review
\(h\)

\(\epsilon\)
\(\xi(\epsilon, W)\)











Many-body Anderson lOCALIZATION Length?
6
Colbois and Laflorencie (2023)
See also Müller & Delande review
\(h\)
The role of interactions
7
\(\epsilon= 1\)
The role of interactions
7
\(\epsilon = 0\)
\(\epsilon= 1\)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
(and many more....)
Ground state, \(\epsilon = 0\)
Interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
The role of interactions
7
\(\epsilon = 0\)
\(\epsilon= 1\)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
(and many more....)
Ground state, \(\epsilon = 0\)
Interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)

The role of interactions
7
\(\epsilon = 0\)
\(\epsilon= 1\)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
(and many more....)
Ground state, \(\epsilon = 0\)
Interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)

Polynomial \(\rightarrow\) Exponential
Absence of translation invariance
No typicality methods
No ground-state methods
24 sites
The role of interactions
7
\(\epsilon = 0\)
\(\epsilon= 1\)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
(and many more....)
Ground state, \(\epsilon = 0\)
Interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)

Polynomial \(\rightarrow\) Exponential
Absence of translation invariance
No typicality methods
No ground-state methods
24 sites
Expectation:
interactions Favor delocalization
The role of interactions
7
\(\epsilon = 0\)
\(\epsilon= 1\)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
(and many more....)
Ground state, \(\epsilon = 0\)
Interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
High energy, \( \epsilon = 0.5\)
Interaction \(\Delta\)
Delocalized
Delocalized
disorder \(h \)
MBL
MBL
Fleischman, Anderson, (1980); Altschuler, et al (1997); Gornyi et al (2005);
Basko et al (2006); Pal and Huse (2010); Luitz et al (2015) [...and a whole field!...]
Localization can survive!

2025
What is many-body localization?
8
Ergodic delocalized
Many-body localized
Entanglement entropy
A
What is many-body localization?
Review: D'Alessio et al. Adv. Phys. (2016)
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ;
Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
8
\(L/2\)
\(S\)
Ergodic delocalized
Many-body localized
Entanglement entropy
A
What is many-body localization?
Review: D'Alessio et al. Adv. Phys. (2016)
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ;
Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
8
Ergodic delocalized
Many-body localized
Entanglement entropy
A
What is many-body localization?
Review: D'Alessio et al. Adv. Phys. (2016)
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ;
Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
\(L/2\)
\(S\)
\(L/2\)
\(S\)
8
\(L/2\)
\(S\)
Ergodic delocalized
Many-body localized
Eigenstates are thermal
Entanglement entropy
A
What is many-body localization?
Review: D'Alessio et al. Adv. Phys. (2016)
Eigenstate thermalization hypothesis
Random matrix theory
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ;
Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
\(L/2\)
\(S\)
8
Ergodic delocalized
Many-body localized
Eigenstates are thermal
Entanglement entropy
A
What is many-body localization?
Review: D'Alessio et al. Adv. Phys. (2016)
Eigenstates are like ground states
Extensive number of quasi-local
conserved quantities
Eigenstate thermalization hypothesis
Random matrix theory
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ;
Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
\(L/2\)
\(S\)
\(L/2\)
\(S\)
Successes of the emergent integrability description
9
Successes of the emergent integrability description
Predicts the eigenstates properties
Serbyn, Papic, Abanin (2013); Bauer, Nayak (2014); Huse, Nandkishore, Oganesyan (2014)
9
Successes of the emergent integrability description
Captures out-of-equilibrium dynamics
Predicts the eigenstates properties
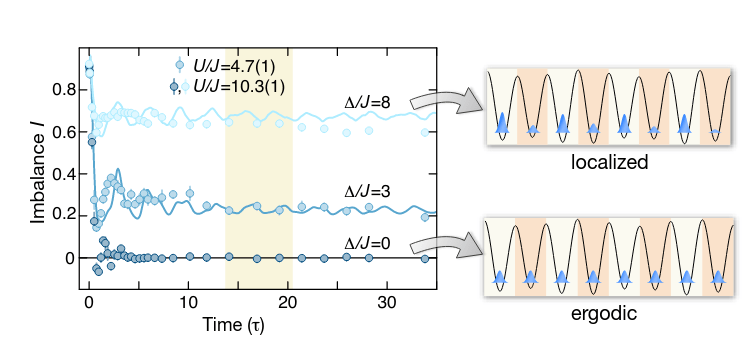
M. Schreiber et al. Science (2015)
Serbyn, Papic, Abanin (2013); Bauer, Nayak (2014); Huse, Nandkishore, Oganesyan (2014)
9
Successes of the emergent integrability description
Supports analytical arguments / proofs
Ros, Müller (2017), Crowley, Chandran (2022), Imbrie (2016), ...
Captures out-of-equilibrium dynamics
Predicts the eigenstates properties

M. Schreiber et al. Science (2015)
Serbyn, Papic, Abanin (2013); Bauer, Nayak (2014); Huse, Nandkishore, Oganesyan (2014)
9
Successes of the emergent integrability description
Anderson insulator
disorder \(h \)
Interaction \(\Delta\)
Ergodic
Many-body localized (?)
9
Successes of the emergent integrability description
Anderson insulator
disorder \(h \)
Interaction \(\Delta\)
Ergodic
Many-body localized (?)
9
Mechanism and nature of the transition to the thermal phase?

Suntajs et al, PRE (2020)
Suntajs et al, PRB (2020)
Panda et al EPL (2019)
Abanin et al (2021)
Sels, Polkovnikov (2021)
LeBlond et al (2021)
Sierant & Zakrewski PRB (2022)
Morningstar et al (2022)
Evers, Modak, Bera (2023)
Long et al (2023)
Ha et al (2023)
Weisse, Gerstner, Sierker (2024)
...
Strong finite-size effects
Ultraslow dynamics
MBL "crisis"
Strong finite-size effects
Ultraslow dynamics

Suntajs et al, PRE (2020)
Suntajs et al, PRB (2020)
Panda et al EPL (2019)
Abanin et al (2021)
Sels, Polkovnikov (2021)
LeBlond et al (2021)
Sierant & Zakrewski PRB (2022)
Morningstar et al (2022)
Evers, Modak, Bera (2023)
Long et al (2023)
Ha et al (2023)
Weisse, Gerstner, Sierker (2024)
...
MBL "crisis"
Instabilities of many-body localization
10
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
11
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
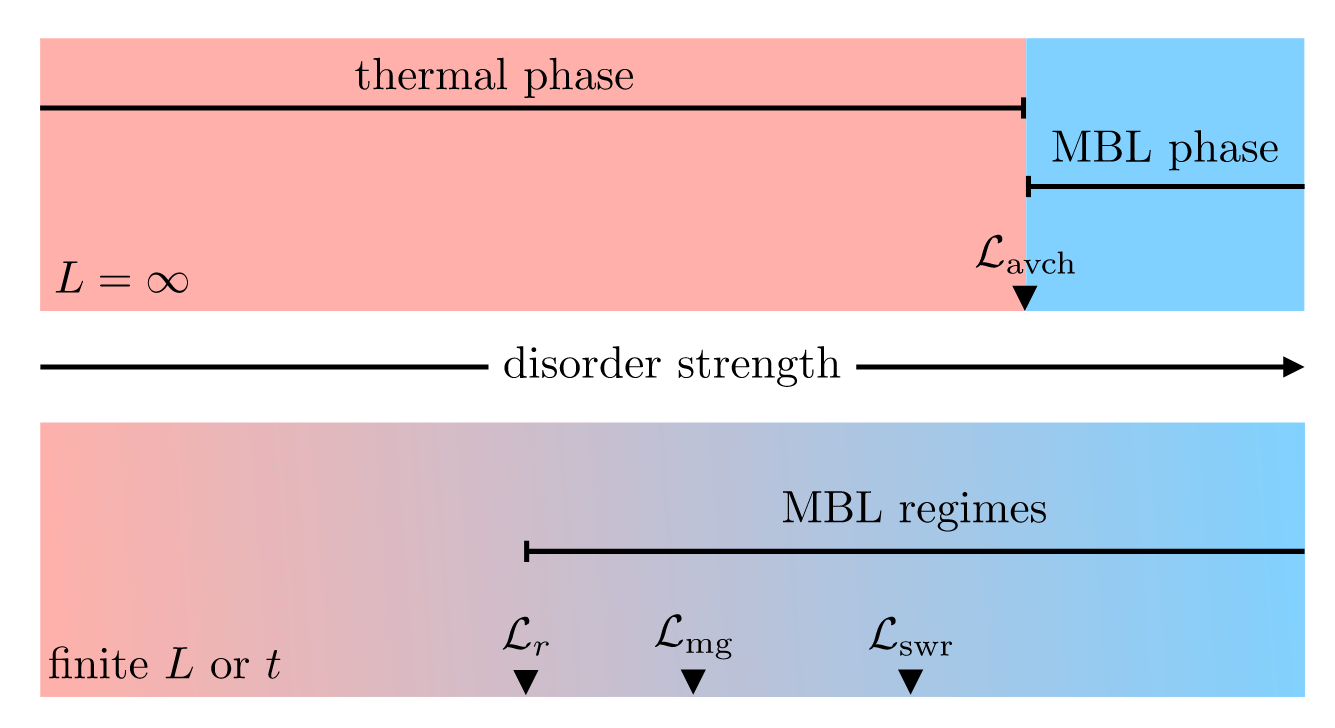
Morningstar et al, PRB 105 (2022)
10
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Morningstar et al, PRB 105 (2022)

Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
avalanche instability
De Roeck & Huveneers (2017), Luitz, De Roeck & Huveneers (2017),
Thiery et al (2018); Crowley and Chandran (2020), Crowley and Chandran (2022)
Small ergodic region triggers runaway delocalization
10
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Morningstar et al, PRB 105 (2022)

many-body resonances
Gopalakrishnan et al (2015)
Villalonga and Clark (2020)
Garratt et al (2021)
Crowley and Chandran (2022)
Morningstar et al (2022)
MBL is destabilized by resonances between localized eigenstates
avalanche instability
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
10
Many-body resonances
11
Resonances between more localized many-body states
Gopalakrishnan et al (2015); Kjäll (2018); Villalonga and Clark (2020); Garratt et al (2021); Crowley and Chandran (2022); Morningstar et al (2022)

Many-body resonances
11
Resonances between more localized many-body states
Gopalakrishnan et al (2015); Kjäll (2018); Villalonga and Clark (2020); Garratt et al (2021); Crowley and Chandran (2022); Morningstar et al (2022)

Many-body resonances
11
Resonances between more localized many-body states
Gopalakrishnan et al (2015); Kjäll (2018); Villalonga and Clark (2020); Garratt et al (2021); Crowley and Chandran (2022); Morningstar et al (2022)

Many-body resonances
11
\(r\)
\(r\)
\(\pm\)
Perturb away from very strong disorder
Resonances between more localized many-body states
Gopalakrishnan et al (2015); Kjäll (2018); Villalonga and Clark (2020); Garratt et al (2021); Crowley and Chandran (2022); Morningstar et al (2022)

Hints in several works but extremely challenging to characterize
12
Two questions
\(h/J \)

Ergodic
MBL
- Can we define a localization length on the non-ergodic side ?
- Can we see traces of "systemwide" resonances ?
\(\Delta/J\)
sTRONG, LONG-RANGE CORRELATIONS AND CAT STATES
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
13
SimplE
Localized
Delocalized
It depends
\(|C^{\alpha,\alpha}_{r} |= A e^{-r /\xi_{\alpha}}\)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
13
SimplE
Experimentally
accessible
Localized
Delocalized
It depends
\(|C^{\alpha,\alpha}_{r} |= A e^{-r /\xi_{\alpha}}\)
\(C_{ij}^{zz} \rightarrow \langle n_i n_{j} \rangle - \langle n_i \rangle \langle n_{j} \rangle\)
From spin to bosons : \(n_i = S_i^{z} + 1/2\)
Density-density correlations
Aubry-André model
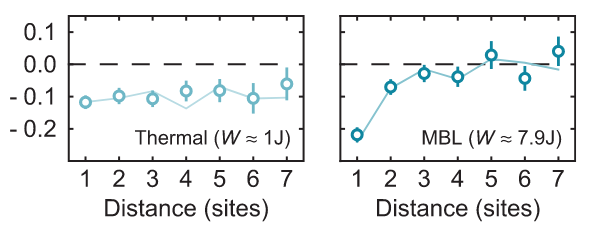
Lukin et al, Science (2019)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
13
SimplE
Experimentally
accessible
Somewhat
overlooked
Localized
Delocalized
It depends
\(|C^{\alpha,\alpha}_{r} |= A e^{-r /\xi_{\alpha}}\)
\(C_{ij}^{zz} \rightarrow \langle n_i n_{j} \rangle - \langle n_i \rangle \langle n_{j} \rangle\)
From spin to bosons : \(n_i = S_i^{z} + 1/2\)
Density-density correlations
Main theoretical works*:
Aubry-André model

Pal & Huse, PRB (2010); Lim, Sheng, PRB (2016)
Localization lengths are short in MBL
Varma et al., PRB (2019)
Character of short-range distributions
Colmenarez et al, SciPost (2019)
*Other works focus on QMI / on weaker disorders / on time evolution
Correlations as a probe of the transition...
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Lukin et al, Science (2019)
13
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
14
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
14
Mid-chain correlations
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
14
Mid-chain correlations
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
14
Mid-chain correlations
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin (dENSITY-DENSITY) Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
14
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
15
15
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
- bulk decay matches mid-chain decay

\(h = 5\)
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
15
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate
15
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate

ONLY SIZE DEPENDENCE!
No spatial dependence,
Random vector
15

Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate

ONLY SIZE DEPENDENCE!
No spatial dependence,
Random vector
15

Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate

Random vector
Total spin conservation
15

Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate

Random vector
Total spin conservation
Random state : XX
finite \(\xi_x\)
15

Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate

Random vector

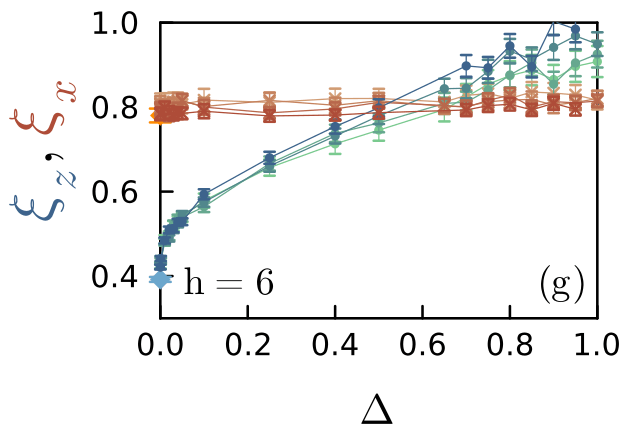
XXZ, \(h = 1, \Delta = 1\)
finite \(\xi_x\)
15

Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector

XXZ, \(h = 1, \Delta = 1\)
finite \(\xi_x\)
15
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate
ZZ correlations dominate


Random vector
XXZ, \(h = 1, \Delta = 1\)
finite \(\xi_x\)
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)

15
14
Random vector
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Inversion of the dominant correlations

16
\(C_{L/2}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+L/2}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+L/2}^{\alpha} \rangle\)
Random vector
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Inversion of the dominant correlations

Extrapolated transition
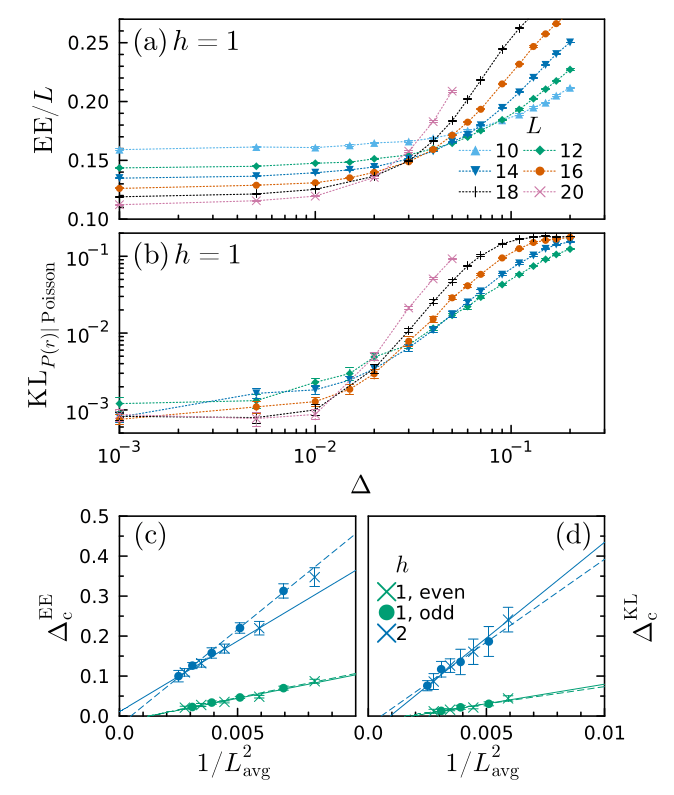
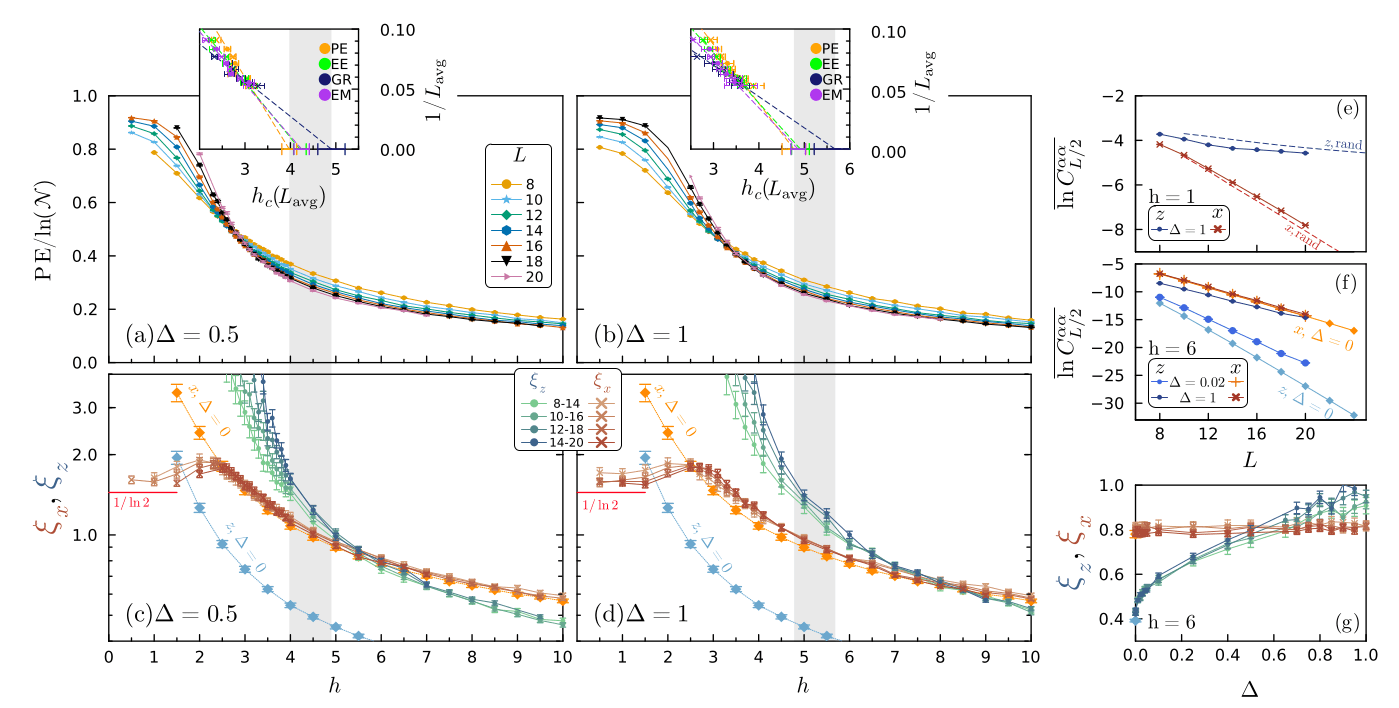
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
14
16
Random vector
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Inversion of the dominant correlations

Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
14
16
Random vector
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Inversion of the dominant correlations

Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
An inversion of the dominant correlations occurs deeper in the MBL regime
Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
14
16
Random vector
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Inversion of the dominant correlations

Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
An inversion of the dominant correlations occurs deeper in the MBL regime
Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
?
14
16
17
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Large correlations along the Heisenberg line

Large correlations along the Heisenberg line

XX
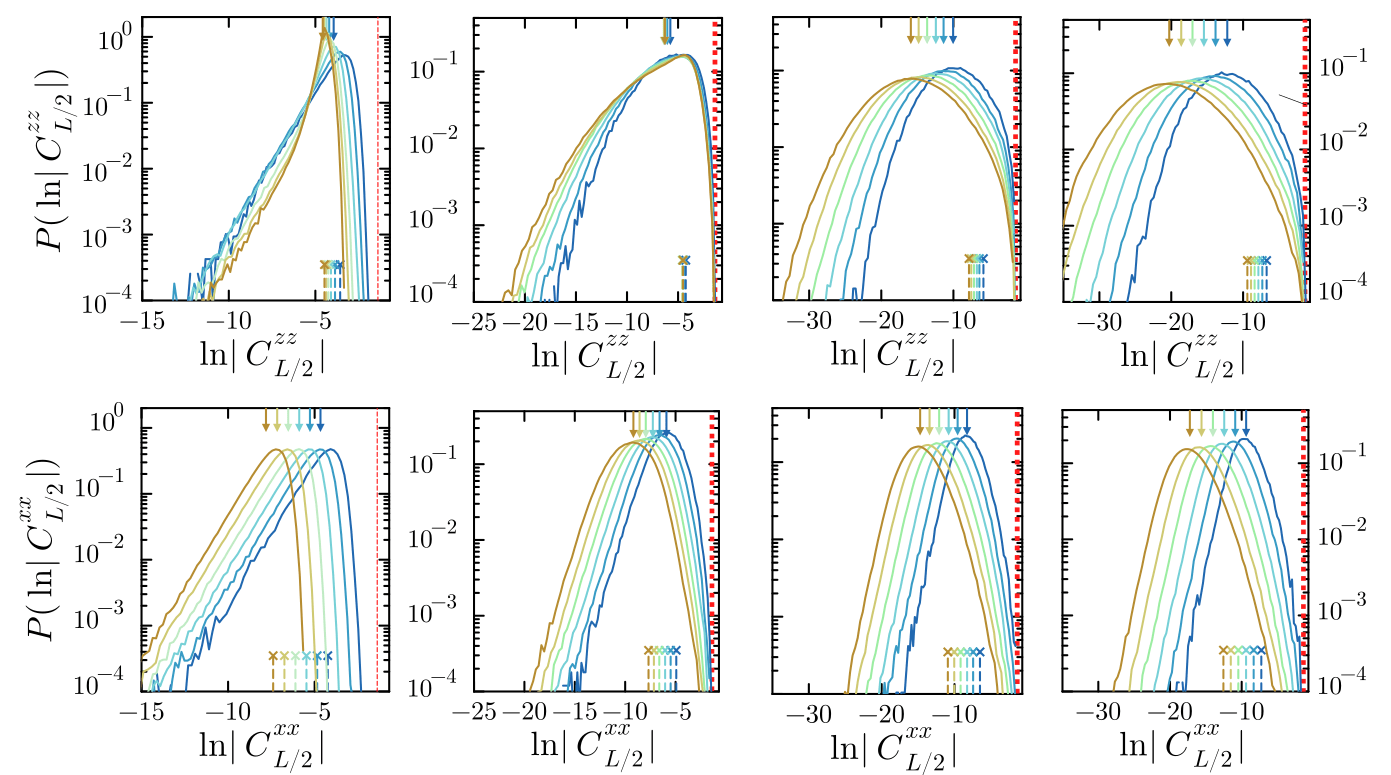
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
17
Large correlations along the Heisenberg line

XX

Limited weight at large correlations
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
17
Large correlations along the Heisenberg line

ZZ

XX
Non-zero probability of large correlations
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Limited weight at large correlations
17
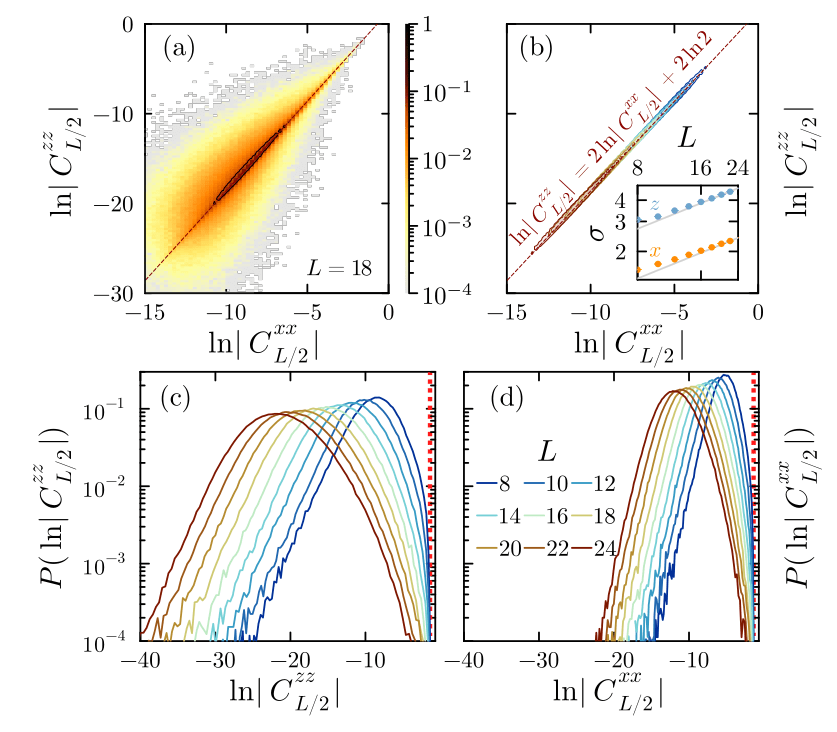
1. Do these rare, large, long-distance correlations matter ?
2. How deep in the MBL phase can we find large correlations ?
3. What are these events ?
18
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
1. Do these large correlations matter ?
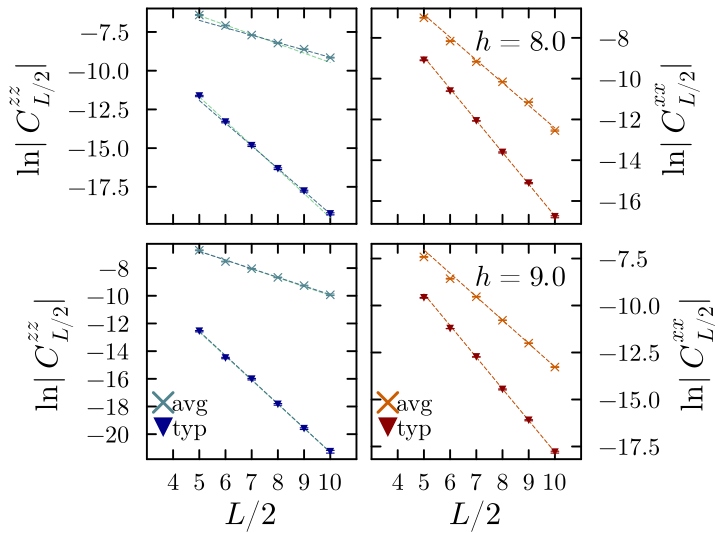

Semi-log
\(C_{L/2}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+L/2}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+L/2}^{\alpha} \rangle\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
1. Do these large correlations matter ?


Semi-log
Average
\(\overline{|C^{zz}_{L/2}|}\)
18
\(C_{L/2}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+L/2}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+L/2}^{\alpha} \rangle\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
1. Do these large correlations matter ?


Average
\(\overline{|C^{zz}_{L/2}|}\)
vs typical
\(\exp(\overline{\ln|C^{zz}_{L/2}|})\)
Semi-log
18
\(C_{L/2}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+L/2}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+L/2}^{\alpha} \rangle\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
1. Do these large correlations matter ?


Average
\(\overline{|C^{zz}_{L/2}|}\)
vs typical
\(\exp(\overline{\ln|C^{zz}_{L/2}|})\)
Semi-log
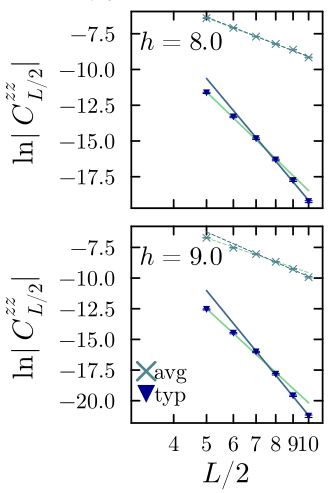

Log-log
18
\(C_{L/2}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+L/2}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+L/2}^{\alpha} \rangle\)
19
2. How deep can we find large correlationS ?
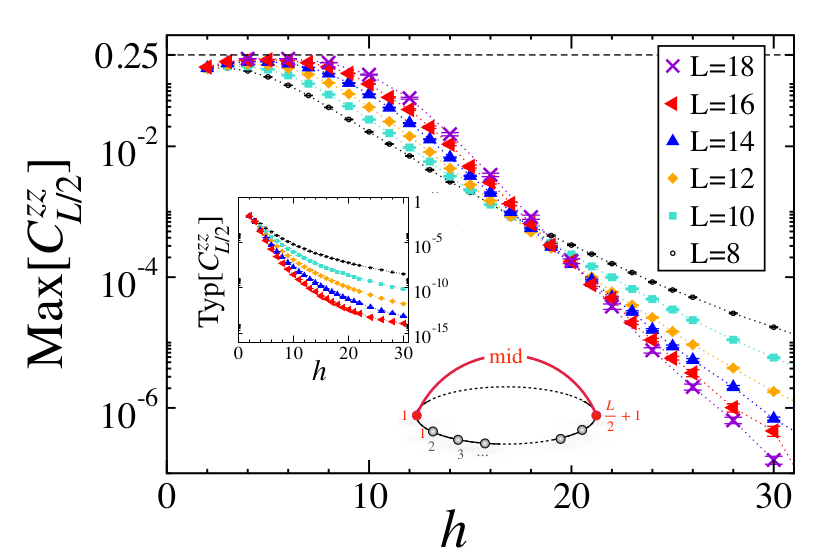
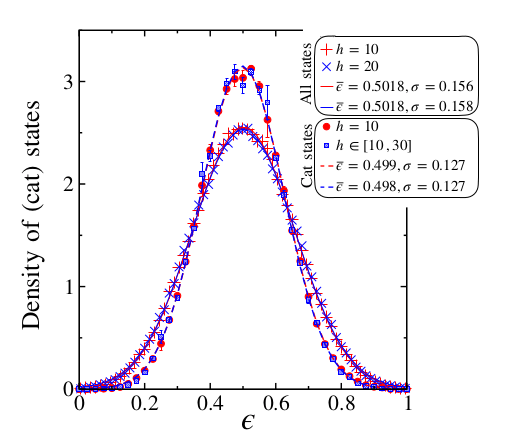
Average of the maximum over all eigenstates
Up to \(h \sim 20-25\)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
20
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
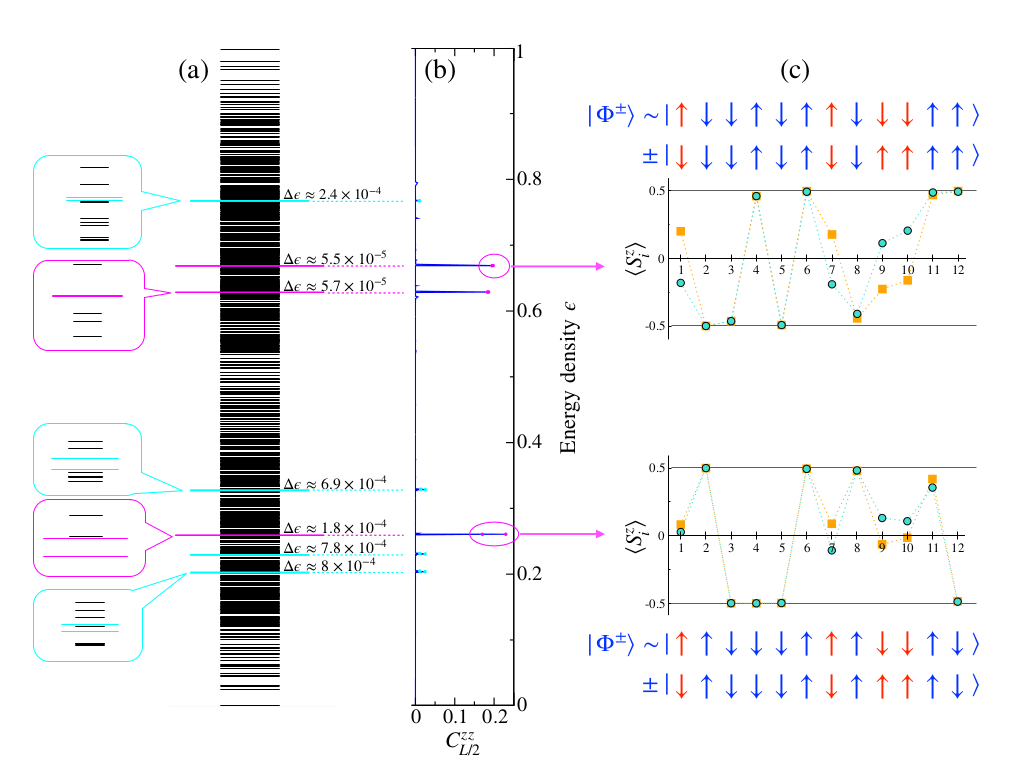
\(L = 20, h = 12\)
3. What are these events?
N. Laflorencie, JC, F. Alet, arXiv:2504.10566

\(L = 20, h = 12\)
3. What are these events?
- Large correlations : pairs
- Extremely small gap
20
N. Laflorencie, JC, F. Alet, arXiv:2504.10566

\(L = 20, h = 12\)
3. What are these events?
- Large correlations : pairs
- Extremely small gap
- Cat states picture

20
21
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
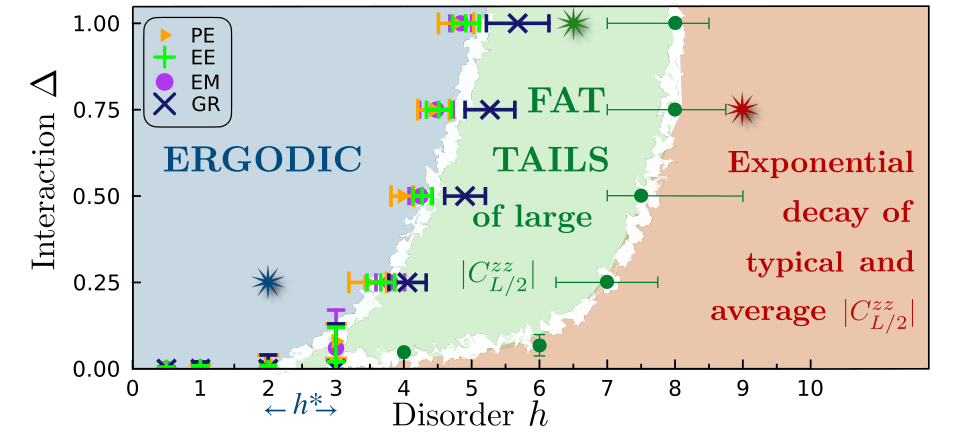
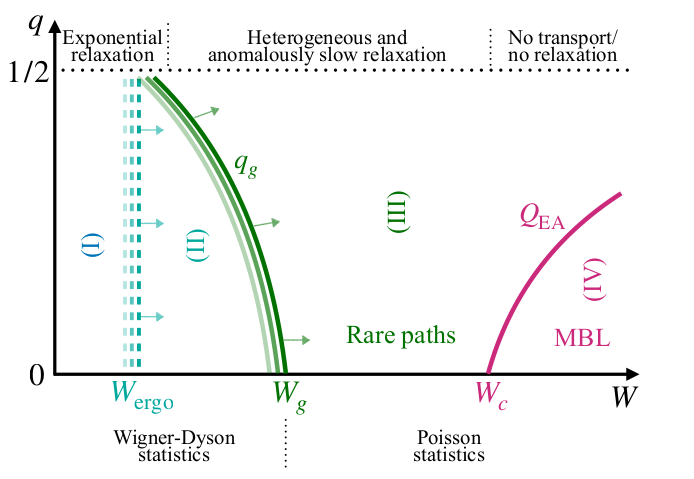
Diagram and questions

Diagram of the correlations regimes:
21
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
Diagram and questions

Diagram of the correlations regimes:
Average: power-law
Average: exponential
21
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
Diagram and questions

Diagram of the correlations regimes:
Particular realizations of disorder?
Unclear because very fine-tuned resonances
Average: power-law
Average: exponential
21
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
Diagram and questions

Diagram of the correlations regimes:
Particular realizations of disorder?
Related to avalanches and rare regions?

Ashirbad Padhan
Unclear because very fine-tuned resonances
Probably not : we find them in quasiperiodic models too!
Average: power-law
Average: exponential
21
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
Diagram and questions

Diagram of the correlations regimes:
Particular realizations of disorder?
Related to avalanches and rare regions?

Unclear because very fine-tuned resonances
Probably not : we find them in quasiperiodic models too!
Can they destabilize MBL?
That is the main question!
Average: power-law
Average: exponential
Ashirbad Padhan
tAKE-HOME MESSAGEs
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Anderson localization
in 1D: \(\forall E\), states are localized
Interactions:
Ergodic (thermal) phase vs. Many-body localization
tAKE-HOME MESSAGEs
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Anderson localization
in 1D: \(\forall E\), states are localized
Interactions:
Ergodic (thermal) phase vs. Many-body localization
OUR CONTRIBUTION:
1. Large correlations at maximal distance deep in the MBL regime.
2. They can dominate the average
3. They signal cat-like states. Toy model to spot them systematically.
Links with dynamics and with Fock space rare events?
Bonus slide unlocked
In the Anderson basis:
Anderson
orbitals \(m\)
JC, F. Alet, N. Laflorencie, PRL, (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)

JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Ergodic
Ergodic
Ergodic
Vertical cut
\(h/J \)


Ergodic
MBL
\(h/J \)


Ergodic
MBL
- \(\xi_{z,x}\) very short
- Directly connected to AL values
- Flat \(\xi_x\), fast increase of \(\xi_z\)
- Instability
Ergodic
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)

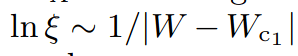
Model : t-V with usual XXZ units, except V = 2t
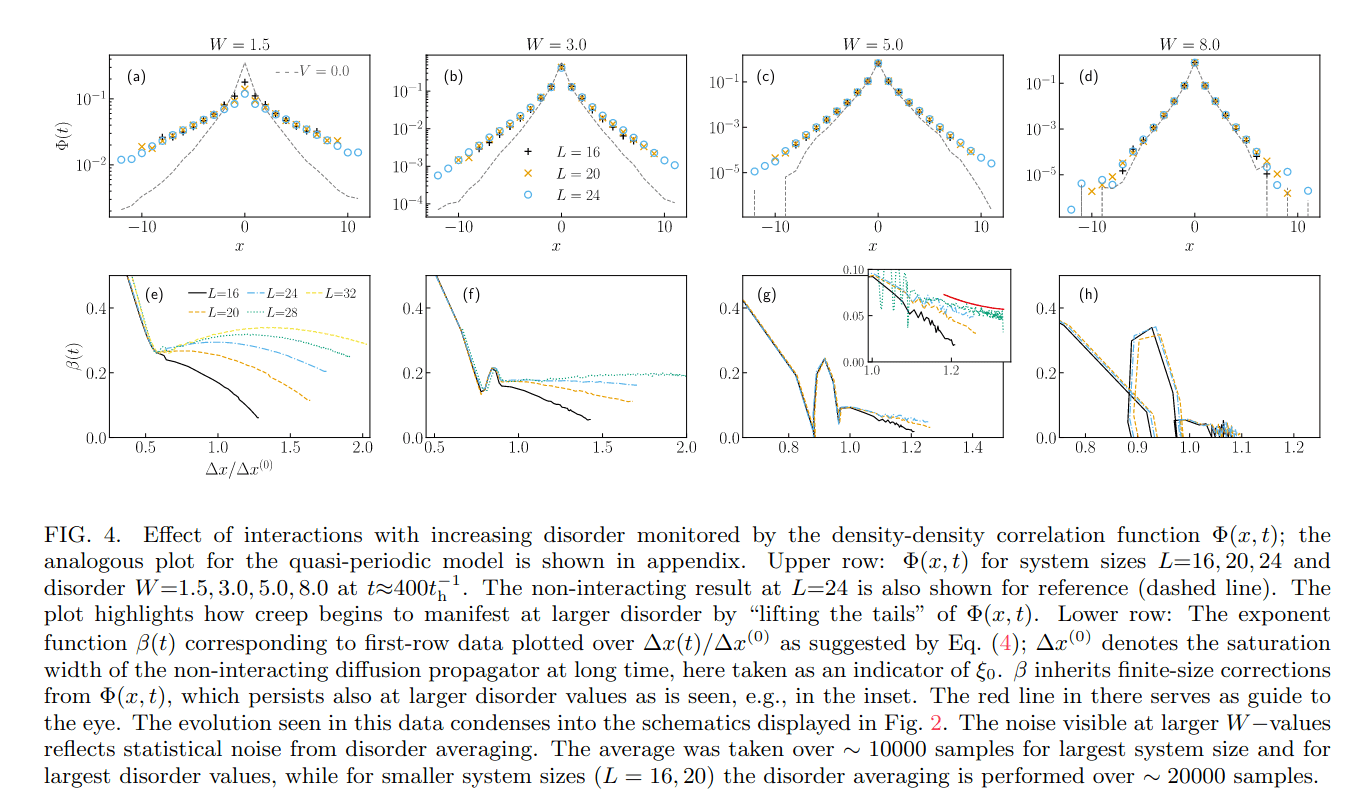

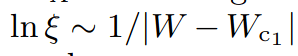
Model : t-V with usual XXZ units, except V = 2t

JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
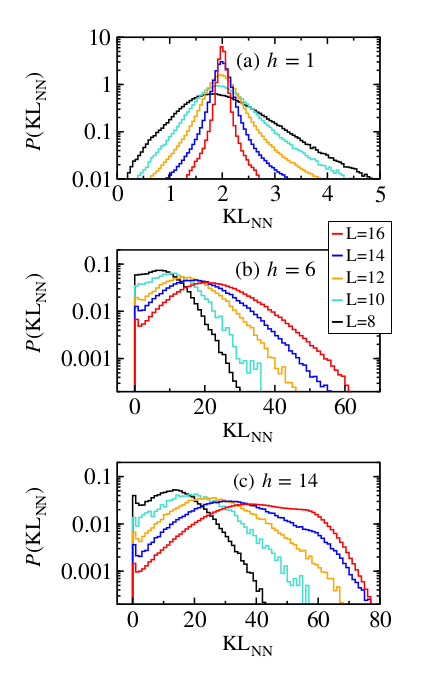
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566
A. Padhan et al. arXiv2510.xxxx
Anderson
No growth
of entanglement
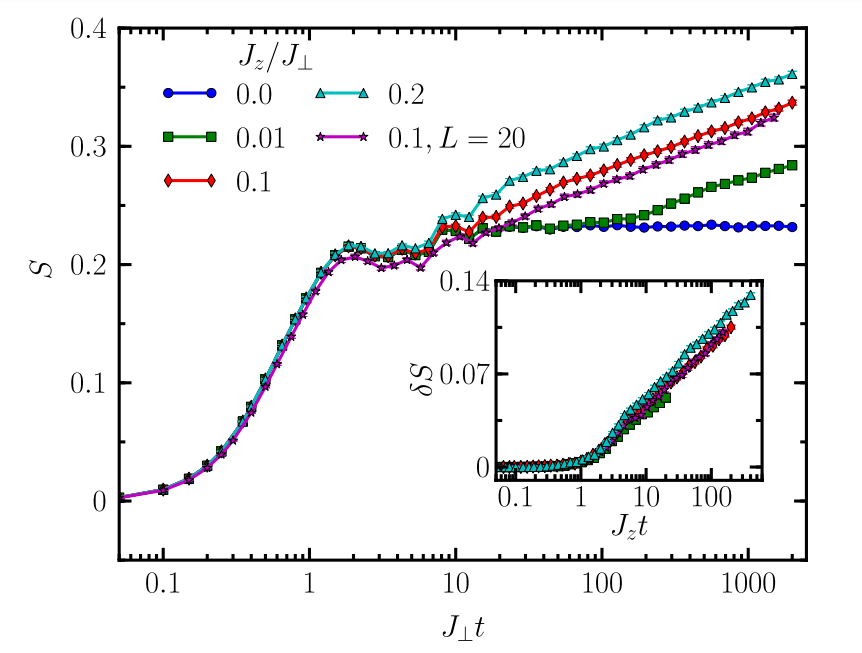
J. H. Bardarson, F. Pollmann, and J. E. Moore, PRL 109, 017202 (2012)
M. Znidaric, T. Prosen, and P. Prelovsek PRB 77, 064426 (2008)
Log growth
of entanglement
Initial \(S^z\) basis random product state
+
TEBD
W = 5