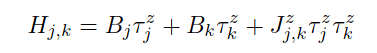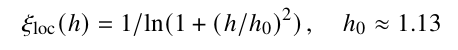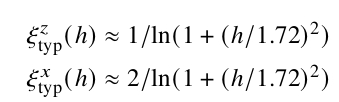Jeanne Colbois | CNRS researcher at Institut NEEL | Grenoble | France
jeanne.colbois@neel.cnrs.fr




From anderson to many-body localization

Jeanne Colbois | CNRS researcher at Institut NEEL | Grenoble | France
jeanne.colbois@neel.cnrs.fr




From anderson to many-body localization

Anderson localization
Jeanne Colbois | CNRS researcher at Institut NEEL | Grenoble | France
jeanne.colbois@neel.cnrs.fr




From anderson to many-body localization

Thermalization in isolated quantum many-body systems
Anderson localization
Jeanne Colbois | CNRS researcher at Institut NEEL | Grenoble | France
jeanne.colbois@neel.cnrs.fr




From anderson to many-body localization
Instabilities in the random field XXZ chain



Nicolas Laflorencie
Fabien Alet
LPT Toulouse - France
Thermalization in isolated quantum many-body systems
Anderson localization
COLBOIS | FROM AL TO MBL | 07.2025
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
1
Conserves \(N_f\)
\(|\psi(x)|^2\)
COLBOIS | FROM AL TO MBL | 07.2025
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
1
Conserves \(N_f\)
\(|\psi(x)|^2\)
\(h\)
\(-h\)
\(h\)
COLBOIS | FROM AL TO MBL | 07.2025
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
1
Conserves \(N_f\)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization !!
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
\(\xi(h, E)\)
COLBOIS | FROM AL TO MBL | 07.2025
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
Constructive interference phenomenon
\(\langle x^{2}(t)\rangle \) saturates : absence of diffusion
1
Conserves \(N_f\)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization !!
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Anderson localization in 1D
Constructive interference phenomenon
\(\langle x^{2}(t)\rangle \) saturates : absence of diffusion
Anderson localization in a many-body setting ?
1
COLBOIS | FROM AL TO MBL | 07.2025
Conserves \(N_f\)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization !!
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
\(\xi(h, E)\)
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
Anderson localization in 1D
Anderson, Phys. Rev. 109, 1492 (1958)
Mott & Twose, Advances in Physics 10, 107 (1961)
\(|\psi(x)|^2\)
\(\forall h , \, \forall E \) : localization !!
(1D, NN)
\(h\)
\(-h\)
\(h\)
\(|\psi(x)|^2\)
Constructive interference phenomenon
\(\langle x^{2}(t)\rangle \) saturates : absence of diffusion
\(\xi(h, E)\)
Anderson localization in a many-body setting ?
1
Absence of thermalization in isolated many-body quantum systems
COLBOIS | FROM AL TO MBL | 07.2025
Conserves \(N_f\)
What may be unusual here:
Quenched disorder
Eigenstates in the middle of the spectrum
2
COLBOIS | FROM AL TO MBL | 07.2025
What may be unusual here:
Quenched disorder
Eigenstates in the middle of the spectrum
... Yet These may ring a bell:
Non-perturbative quantum many-body physics on a lattice
Entanglement
(Random matrix theory ?)
2
COLBOIS | FROM AL TO MBL | 07.2025
3
Scope
1. From "many-body" Anderson localization to the question
2. Thermalization of isolated quantum systems
COLBOIS | FROM AL TO MBL | 07.2025
3
Scope
1. From "many-body" Anderson localization to the question
2. Thermalization of isolated quantum systems
On a spin chain:
3. Many-body localization vs thermalization
4. The MBL "crisis"
COLBOIS | FROM AL TO MBL | 07.2025
3
Scope
1. From "many-body" Anderson localization to the question
2. Thermalization of isolated quantum systems
On a spin chain:
3. Many-body localization vs thermalization
4. The MBL "crisis"
5. Avalanche instability at weak interactions
6. Resonances through correlations
COLBOIS | FROM AL TO MBL | 07.2025
1. "Many-body" Anderson localization
4
Several non-interacting fermions
COLBOIS | FROM AL TO MBL | 07.2025
Conserves \(N_f\)
4
Several non-interacting fermions
COLBOIS | FROM AL TO MBL | 07.2025
Conserves \(N_f\)
commute with
commute with each other
(quasi-)local
\(L\) quasi-local integrals of motion
5
Several non-interacting fermions
Slater determinant based on quasi-local wavefunctions
\(\xi(h, E)\)










COLBOIS | FROM AL TO MBL | 07.2025
Conserves \(N_f\)
Several non-interacting fermions
Slater determinant based on quasi-local wavefunctions
\(\xi(h, E)\)










COLBOIS | FROM AL TO MBL | 07.2025
in AL in 1D, ALL EigenSTATES ARE LIKE GROUND STATES
Conserves \(N_f\)
5
6
"Area-law" of entanglement
A
\(\rho_A = \mathrm{Tr}_B | \Psi \rangle \langle \Psi |\)
COLBOIS | FROM AL TO MBL | 07.2025
\(\{| n_1, n_2, \dots, n_B \rangle \}\)
6
A
\(\rho_A = \mathrm{Tr}_B | \Psi \rangle \langle \Psi |\)
\(\{| n_1, n_2, \dots, n_B \rangle \}\)
COLBOIS | FROM AL TO MBL | 07.2025
\(S = -\mathrm{Tr} \rho_A \ln \rho_A\)
Von-Neumann EE
"Area-law" of entanglement
6
\(S = -\mathrm{Tr} \rho_A \ln \rho_A\)
A
\(\rho_A = \mathrm{Tr}_B | \Psi \rangle \langle \Psi |\)
Von-Neumann EE
\(\{| n_1, n_2, \dots, n_B \rangle \}\)
Entanglement entropy controlled by the boundary
(exponentially small contribution from the bulk)










COLBOIS | FROM AL TO MBL | 07.2025
"Area-law" of entanglement
7
Poisson spectral statistics
Gap ratio:
COLBOIS | FROM AL TO MBL | 07.2025
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
7
Poisson spectral statistics
Gap ratio:










COLBOIS | FROM AL TO MBL | 07.2025
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
7
Gap ratio:
Single-body:
\(P(r)\)
\(r\)
1. Limit \(h \gg J\) : \(E_i\) random \(\rightarrow\) Poisson










COLBOIS | FROM AL TO MBL | 07.2025
Poisson spectral statistics
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
7
Gap ratio:
Single-body:
\(P(r)\)
\(r\)
1. Limit \(h \gg J\) : \(E_i\) random \(\rightarrow\) Poisson










COLBOIS | FROM AL TO MBL | 07.2025
2. Smaller disorder : \(\rightarrow\) still Poisson
Poisson spectral statistics
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
7
Gap ratio:
Single-body:
Many-body (high in the spectrum)
\(P(r)\)
\(r\)
1. Limit \(h \gg J\) : \(E_i\) random \(\rightarrow\) Poisson
2. Smaller disorder : \(\rightarrow\) still Poisson










3. Neighbouring \(\mathcal{E}_n\) correspond to very different \(\sum E_m\)
COLBOIS | FROM AL TO MBL | 07.2025
Poisson spectral statistics
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
7
Gap ratio:
Single-body:
Many-body (high in the spectrum)
\(P(r)\)
\(r\)
1. Limit \(h \gg J\) : \(E_i\) random \(\rightarrow\) Poisson
2. Smaller disorder : \(\rightarrow\) still Poisson










3. Neighbouring \(\mathcal{E}_n\) correspond to very different \(\sum E_m\)
Neighbouring eigenstates have little in common
COLBOIS | FROM AL TO MBL | 07.2025
Poisson spectral statistics
8
An old question
Does 1D Anderson localization "survive" interactions?
Attraction / repulsion
\(-h\)
\(h\)
at high energy
COLBOIS | FROM AL TO MBL | 07.2025
8
An old question
Does 1D Anderson localization "survive" interactions?
In the Anderson basis:
Anderson orbitals \(m\)
Attraction / repulsion
\(-h\)
\(h\)
at high energy
COLBOIS | FROM AL TO MBL | 07.2025
8
An old question
Does 1D Anderson localization "survive" interactions?
In the Anderson basis:
Anderson orbitals \(m\)
Attraction / repulsion
\(-h\)
\(h\)
at high energy
COLBOIS | FROM AL TO MBL | 07.2025
Interactions favor delocalization. Do they fully destroy localization?
2. Why we care :
Can isolated quantum systems thermalize ?
What is (quantum) thermalization ?
COLBOIS | FROM AL TO MBL | 07.2025
9
Isolated
many-body system
?
Description with statistical mechanics
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
What is (quantum) thermalization ?
COLBOIS | FROM AL TO MBL | 07.2025
9
Isolated
many-body system
?
Description with statistical mechanics
Long-time average of few-body observables
Microcanonical average
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
What is (quantum) thermalization ?
COLBOIS | FROM AL TO MBL | 07.2025
9
Isolated
many-body system
?
Description with statistical mechanics
Long-time average of few-body observables
Microcanonical average
Unitary time evolution
Long-time behavior completely controlled by eigenstates
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
Eigenstate thermalization hypothesis
COLBOIS | FROM AL TO MBL | 07.2025
10
A sufficient condition on eigenstates
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
Eigenstate thermalization hypothesis
COLBOIS | FROM AL TO MBL | 07.2025
10
A sufficient condition on eigenstates
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
Eigenstate thermalization hypothesis
COLBOIS | FROM AL TO MBL | 07.2025
10
A sufficient condition on eigenstates
Smooth function
Equal to microcanonical average
Equilibrium
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
Eigenstate thermalization hypothesis
COLBOIS | FROM AL TO MBL | 07.2025
10
A sufficient condition on eigenstates
Smooth function
Equal to microcanonical average
Entropy
Smooth
Random variable
Approach to equilibrium
Equilibrium
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
Eigenstate thermalization hypothesis
COLBOIS | FROM AL TO MBL | 07.2025
10
A sufficient condition on eigenstates
Smooth function
Equal to microcanonical average
Entropy
Smooth
Random variable
Approach to equilibrium
Equilibrium
Narrow energy window: random matrix theory
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
Eigenstate thermalization hypothesis
COLBOIS | FROM AL TO MBL | 07.2025
10
A sufficient condition on eigenstates
Smooth function
Equal to microcanonical average
Entropy
Smooth
Random variable
Approach to equilibrium
Equilibrium
Eigenstates are thermal (rDM indistinguishable from thermal)
neighbouring eigenstates are similar
Narrow energy window: random matrix theory
Deutsch (1991), Srednicki (1994)
D'Alessio et al (2016) for a review
3. Many-body localization vs thermalization
In a spin chain model
3. Many-body localization vs thermalization
In a spin chain model

2015

2018


2019

2025
3
3
11
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
COLBOIS | FROM AL TO MBL | 07.2025
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
Attraction / repulsion
3
3
11
COLBOIS | FROM AL TO MBL | 07.2025
3
3
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)
3
3
11
COLBOIS | FROM AL TO MBL | 07.2025
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
\(n_i = S_i^z + 1/2\)
\(c_i = \exp(i \pi \sum_{j=1}^{i-1} n_j) S_i^{-}\)
non-local transformation
Spin-flip
P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)
3
3
11
COLBOIS | FROM AL TO MBL | 07.2025
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
ISING INTERACTION
Spin-flip
P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)
\(n_i = S_i^z + 1/2\)
\(c_i = \exp(i \pi \sum_{j=1}^{i-1} n_j) S_i^{-}\)
3
3
11
COLBOIS | FROM AL TO MBL | 07.2025
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
ISING INTERACTION
Spin-flip
P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)
\(n_i = S_i^z + 1/2\)
\(c_i = \exp(i \pi \sum_{j=1}^{i-1} n_j) S_i^{-}\)
3
3
11
COLBOIS | FROM AL TO MBL | 07.2025
From fermions to spins : JorDan-Wigner
\(-h\)
\(h\)
Attraction / repulsion
Jordan-Wigner
non-local transformation
ISING INTERACTION
Spin-flip
P. Jordan and E. Wigner, Z. Physik 47, 631–651 (1928)
\(n_i = S_i^z + 1/2\)
\(c_i = \exp(i \pi \sum_{j=1}^{i-1} n_j) S_i^{-}\)
3
3
11
\(L/2\) fermions
Charge is conserved
\(\sum_i S_i^{z} = 0\)
Magnetization is conserved
COLBOIS | FROM AL TO MBL | 07.2025
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
3
3
12
COLBOIS | FROM AL TO MBL | 07.2025
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
\(\epsilon = 1\)
\(\epsilon = 0\)
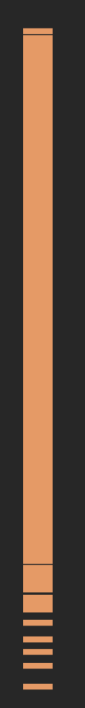
Ground state, \(\epsilon = 0\)
Ising interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
Ristivojevic, et al PRL 109, (2012);
Doggen et al, PRB 96, (2017);
Lin et al, Scipost Phys 4 (2019)
3
3
12
COLBOIS | FROM AL TO MBL | 07.2025
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
\(\epsilon = 1\)
\(\epsilon = 0\)
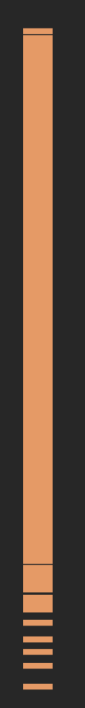
Ground state, \(\epsilon = 0\)
Ising interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
Ristivojevic, et al PRL 109, (2012);
Doggen et al, PRB 96, (2017);
Lin et al, Scipost Phys 4 (2019)
3
3
12
COLBOIS | FROM AL TO MBL | 07.2025
Counter example for thermalization of isolated quantum systems
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
\(\epsilon = 1\)
\(\epsilon = 0\)
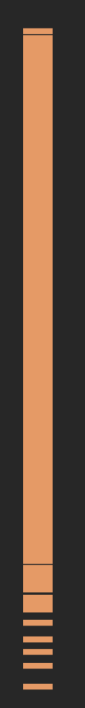
Ground state, \(\epsilon = 0\)
Ising interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
Ristivojevic, et al PRL 109, (2012);
Doggen et al, PRB 96, (2017);
Lin et al, Scipost Phys 4 (2019)
Counter example for thermalization of isolated quantum systems

Polynomial \(\rightarrow\) Exponential
Absence of translation invariance
No typicality methods
No ground-state methods
3
3
12
COLBOIS | FROM AL TO MBL | 07.2025
\(\epsilon = 1\)
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
\(\epsilon = 1\)
\(\epsilon = 0\)
Ground state, \(\epsilon = 0\)
Ising interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
Ristivojevic, et al PRL 109, (2012);
Doggen et al, PRB 96, (2017);
Lin et al, Scipost Phys 4 (2019)
Counter example for thermalization of isolated quantum systems

Polynomial \(\rightarrow\) Exponential
Absence of translation invariance
No typicality methods
No ground-state methods
Expectation:
interactions delocalize
3
3
13
COLBOIS | FROM AL TO MBL | 07.2025
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
\(\epsilon = 1\)
\(\epsilon = 0\)
Ground state, \(\epsilon = 0\)
Ising interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
Ristivojevic, et al PRL 109, (2012);
Doggen et al, PRB 96, (2017);
Lin et al, Scipost Phys 4 (2019)
Counter example for thermalization of isolated quantum systems
High energy, \( \epsilon = 0.5\)
Ising interaction \(\Delta\)
Delocalized
Delocalized
disorder \(h \)
MBL
MBL
.... and a whole field! ....
Fleischman, Anderson, (1980); Altschuler, et al (1997); Gornyi et al (2005); Basko et al (2006); Zidnarick et al (2008); Aleiner et al (2010); Pal and Huse (2010); Luitz et al (2015) [....]
Localization can survive!
3
3
13
COLBOIS | FROM AL TO MBL | 07.2025
ISING INTERACTION
Is 1D AL Preserved under interactions (in spin chains) ?
Spin-flip
\(\epsilon = 1\)
\(\epsilon = 0\)
Ground state, \(\epsilon = 0\)
Ising interaction \(\Delta\)
Localized
Delocalized
disorder \(h \)
Giamarchi & Schulz EPL 3 (1987); PRB 37, (1988);
Ristivojevic, et al PRL 109, (2012);
Doggen et al, PRB 96, (2017);
Lin et al, Scipost Phys 4 (2019)
Counter example for thermalization of isolated quantum systems
High energy, \( \epsilon = 0.5\)
Ising interaction \(\Delta\)
Delocalized
Delocalized
disorder \(h \)
MBL
MBL
.... and a whole field! ....
Fleischman, Anderson, (1980); Altschuler, et al (1997); Gornyi et al (2005); Basko et al (2006); Zidnarick et al (2008); Aleiner et al (2010); Pal and Huse (2010); Luitz et al (2015) [....]
Localization can survive!
?
3
3
13
COLBOIS | FROM AL TO MBL | 07.2025
From thermalization to many-body localization
Disorder
\(\Delta > 0\)
3
3
14
COLBOIS | FROM AL TO MBL | 07.2025
From thermalization to many-body localization
Disorder
\(\Delta > 0\)
Ergodic delocalized
3
3
14
COLBOIS | FROM AL TO MBL | 07.2025
From thermalization to many-body localization
Disorder
\(\Delta > 0\)
Ergodic delocalized
Many-body localized
3
3
14
COLBOIS | FROM AL TO MBL | 07.2025
From thermalization to many-body localization
Ergodic delocalized
Many-body localized
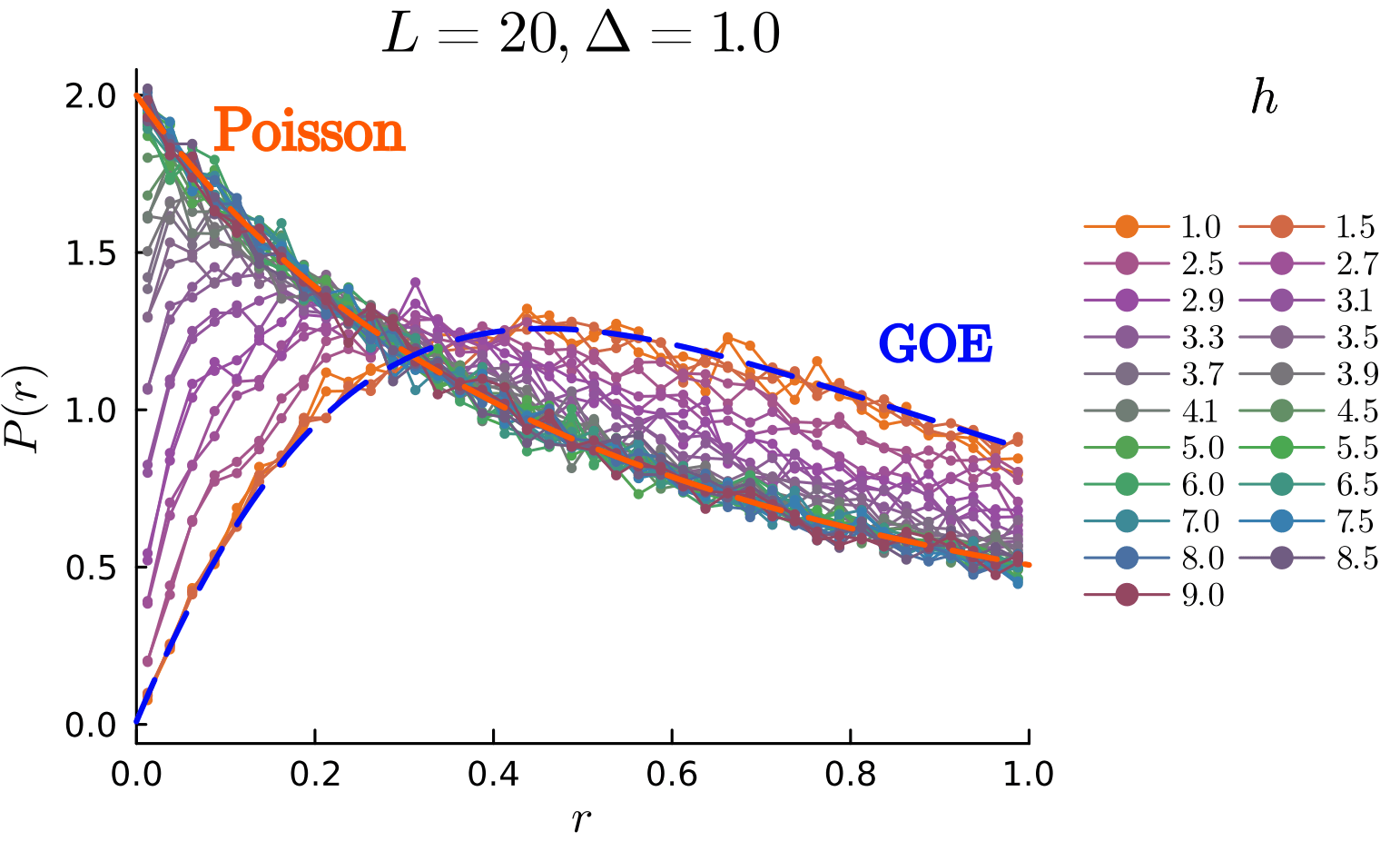
Spectral statistics
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
Disorder
\(\Delta > 0\)
3
3
14
COLBOIS | FROM AL TO MBL | 07.2025
From thermalization to many-body localization
Many-body localized
Spectral statistics
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
Disorder
\(\Delta > 0\)

\(r\)
\(P(r)\)
GOE = Ergodic
3
3
14
COLBOIS | FROM AL TO MBL | 07.2025
Ergodic delocalized
Text
Random matrix theory
From thermalization to many-body localization
Many-body localized
Spectral statistics
P. Jacquod, D. L. Shepelyansky, PRL 79, 1837 (1997) [... a lot of works ...]
O. Giraud, N. Macé, E. Vernier, F. Alet, PRX 12, 011006 (2022)
Disorder
\(\Delta > 0\)

GOE = Ergodic
\(r\)
\(P(r)\)
\(P(r)\)
Poisson = localized
3
3
14
COLBOIS | FROM AL TO MBL | 07.2025
Ergodic delocalized
Random matrix theory
From thermalization to many-body localization
Many-body localized
Disorder
\(\Delta > 0\)
Entanglement entropy
A
\(r\)
\(P(r)\)
\(P(r)\)

Khemani et al, PRX 7 (2017)
Disorder \(h\)
3
3
15
COLBOIS | FROM AL TO MBL | 07.2025
Ergodic delocalized
From thermalization to many-body localization
Many-body localized
Disorder
\(\Delta > 0\)
Entanglement entropy
A
\(r\)
\(P(r)\)
\(P(r)\)


Volume-law at weak disorder
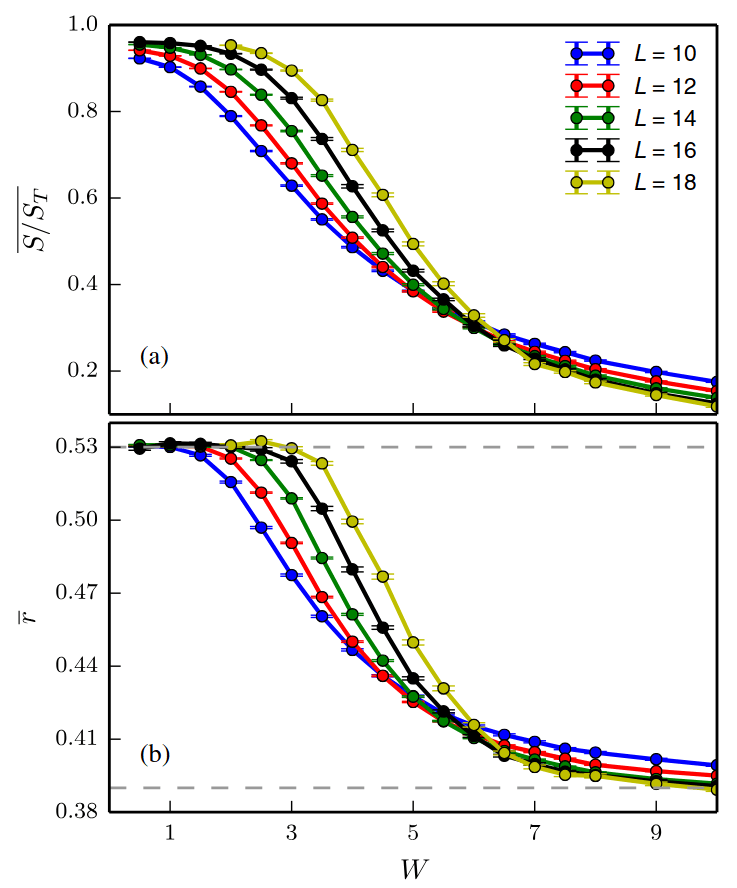
Khemani et al, PRX 7 (2017)
Disorder \(h\)
\(L/2\)
\(S/L\)
\(S_T = (L-\log_2(e))/2\)
3
3
15
COLBOIS | FROM AL TO MBL | 07.2025
Ergodic delocalized
Eigenstates are thermal
From thermalization to many-body localization
Many-body localized
Disorder
\(\Delta > 0\)
Entanglement entropy
A
\(r\)
\(P(r)\)
\(P(r)\)


Area-law at strong disorder
Volume-law at weak disorder
Khemani et al, PRX 7 (2017)
Disorder \(h\)
\(L/2\)
\(S/L\)
\(S_T = (L-\log_2(e))/2\)
3
3
15
\(L/2\)
\(S/L\)
COLBOIS | FROM AL TO MBL | 07.2025
Ergodic delocalized
Eigenstates are thermal
3
3
16
is MBL different from AL ?
Initial \(S^z\) basis random product state
+
time evolution \(h = 5\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
16
is MBL different from AL ?
Initial \(S^z\) basis random product state
+
time evolution \(h = 5\)
COLBOIS | FROM AL TO MBL | 07.2025
J. H. Bardarson, F. Pollmann, and J. E. Moore, PRL 109, 017202 (2012)
M. Znidaric, T. Prosen, and P. Prelovsek PRB 77, 064426 (2008)
3
3
16
is MBL different from AL ?
Anderson
No growth
of entanglement
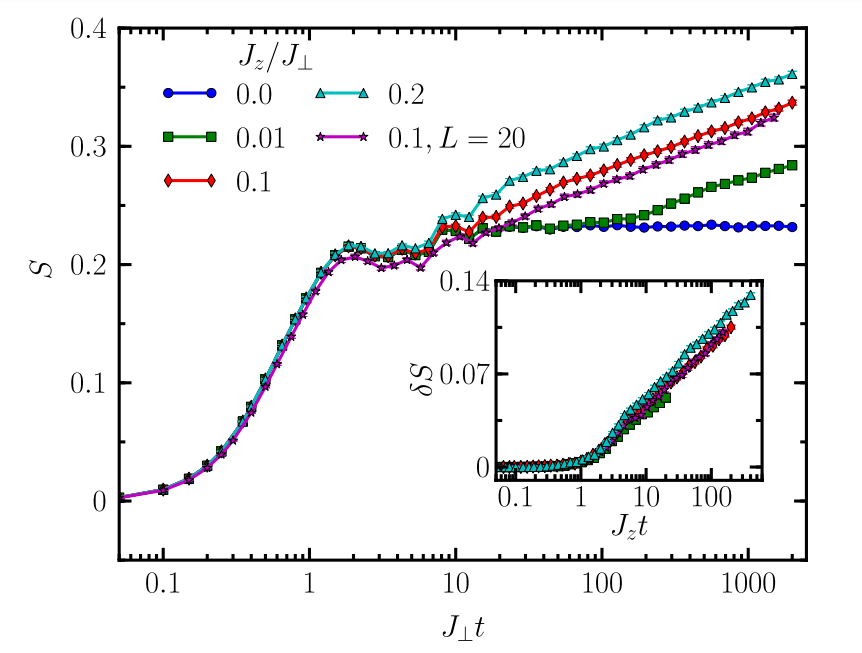
J. H. Bardarson, F. Pollmann, and J. E. Moore, PRL 109, 017202 (2012)
M. Znidaric, T. Prosen, and P. Prelovsek PRB 77, 064426 (2008)
Initial \(S^z\) basis random product state
+
time evolution \(h = 5\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
16
is MBL different from AL ?
Anderson
No growth
of entanglement

J. H. Bardarson, F. Pollmann, and J. E. Moore, PRL 109, 017202 (2012)
M. Znidaric, T. Prosen, and P. Prelovsek PRB 77, 064426 (2008)
MBL
Log growth
of entanglement
Initial \(S^z\) basis random product state
+
time evolution \(h = 5\)
COLBOIS | FROM AL TO MBL | 07.2025
PhenomenoloGY : Emergent integrability
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

When MBL : \(J_{i,...,j} \propto e^{-\frac{-|i-j|}{\zeta}}\)
PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

When MBL : \(J_{i,...,j} \propto e^{-\frac{-|i-j|}{\zeta}}\)

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- out of equilibrium dynamics
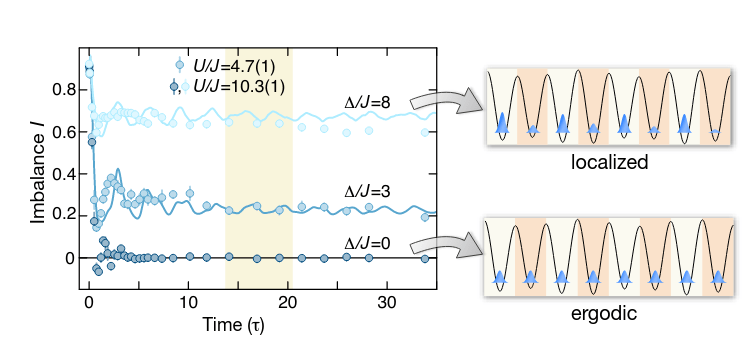
M. Schreiber et al. Science (2015)
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

When MBL : \(J_{i,...,j} \propto e^{-\frac{-|i-j|}{\zeta}}\)

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- out of equilibrium dynamics

M. Schreiber et al. Science (2015)
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

When MBL : \(J_{i,...,j} \propto e^{-\frac{-|i-j|}{\zeta}}\)

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
- log-growth of EE

J. H. Bardarson et al, PRL 109, 017202 (2012)
M. Znidaric et al PRB 77, 064426 (2008)
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- out of equilibrium dynamics

M. Schreiber et al. Science (2015)
- log-growth of EE

J. H. Bardarson et al, PRL 109, 017202 (2012)
M. Znidaric et al PRB 77, 064426 (2008)
- analytical arguments / proof(s)
- Basko, Aleiner, Altschuler (2006), Ros, Müller (2017), Crowley, Chandran (2022),
- Imbrie (2016), ...
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

When MBL : \(J_{i,...,j} \propto e^{-\frac{-|i-j|}{\zeta}}\)

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
Serbyn, Papic, Abanin (2013) ; Bauer, Nayak (2014) ; Huse, Nandkishore, Oganesyan (2014)
Reviews : Imbrie, Ros, Scardicchio (2017) Rademarker, Ortuno, Somoza (2017)
- out of equilibrium dynamics

M. Schreiber et al. Science (2015)
- log-growth of EE

J. H. Bardarson et al, PRL 109, 017202 (2012)
M. Znidaric et al PRB 77, 064426 (2008)
- analytical arguments / proof(s)
mechanism behind the transition ?
- Basko, Aleiner, Altschuler (2006), Ros, Müller (2017), Crowley, Chandran (2022),
- Imbrie (2016), ...
- \(L\) commuting operators, commuting with \(\mathcal{H}\)
- quasi-local

When MBL : \(J_{i,...,j} \propto e^{-\frac{-|i-j|}{\zeta}}\)

PhenomenoloGY : Emergent integrability
Interacting model
COLBOIS | FROM AL TO MBL | 07.2025
3
3
17
AL : L quasilocal conserved quantities
As of 2016

4. MBL "Crisis"
Strong finite-size effects
Ultraslow dynamics
Theory of instabilities

Suntajs et al, PRE (2020)
Suntajs et al, PRB (2020)
Panda et al EPL (2019)
Abanin et al (2021)
Sels, Polkovnikov (2021)
LeBlond et al (2021)
Sierant & Zakrewski PRB (2022)
Morningstar et al (2022)
Evers, Modak, Bera (2023)
Long et al (2023)
Ha et al (2023)
Weisse, Gerstner, Sierker (2024)
...
4. MBL "Crisis"
Strong finite-size effects
Ultraslow dynamics
Theory of instabilities

2025

Suntajs et al, PRE (2020)
Suntajs et al, PRB (2020)
Panda et al EPL (2019)
Abanin et al (2021)
Sels, Polkovnikov (2021)
LeBlond et al (2021)
Sierant & Zakrewski PRB (2022)
Morningstar et al (2022)
Evers, Modak, Bera (2023)
Long et al (2023)
Ha et al (2023)
Weisse, Gerstner, Sierker (2024)
...
4. MBL "Crisis"
Strong finite-size effects
Ultraslow dynamics
Theory of instabilities

2025

Suntajs et al, PRE (2020)
Suntajs et al, PRB (2020)
Panda et al EPL (2019)
Abanin et al (2021)
Sels, Polkovnikov (2021)
LeBlond et al (2021)
Sierant & Zakrewski PRB (2022)
Morningstar et al (2022)
Evers, Modak, Bera (2023)
Long et al (2023)
Ha et al (2023)
Weisse, Gerstner, Sierker (2024)
...
4. MBL "Crisis"
Strong finite-size effects
Ultraslow dynamics
Theory of instabilities

2025

Suntajs et al, PRE (2020)
Suntajs et al, PRB (2020)
Panda et al EPL (2019)
Abanin et al (2021)
Sels, Polkovnikov (2021)
LeBlond et al (2021)
Sierant & Zakrewski PRB (2022)
Morningstar et al (2022)
Evers, Modak, Bera (2023)
Long et al (2023)
Ha et al (2023)
Weisse, Gerstner, Sierker (2024)
...
4. MBL "Crisis"
Some examples of Strong finite-size effects
3
3
17
COLBOIS | FROM AL TO MBL | 07.2025
Some examples of Strong finite-size effects
Gap Ratio
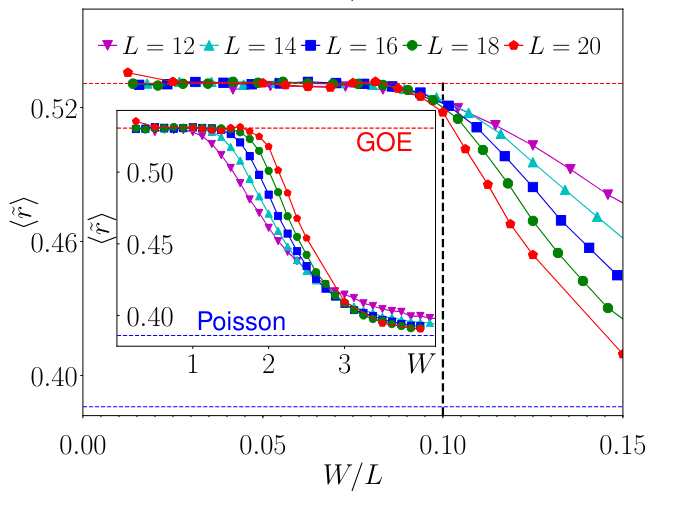
Challenging finite-size scaling
\(h/L\)
\(h\)
Suntajs et al (2020)
(arXiv v1-v2)
3
3
18
COLBOIS | FROM AL TO MBL | 07.2025
Some examples of Strong finite-size effects
Gap Ratio
Sierant, Lewenstein, Zakrewski PRL (2020)

Suntajs et al (2020)
(arXiv v1-v2)
Challenging finite-size scaling
Disorder \(h\)
Disorder \(h\)
\(h/L\)
\(h\)
3
3
18
COLBOIS | FROM AL TO MBL | 07.2025
Some examples of Strong finite-size effects

Gap Ratio
Sierant, Lewenstein, Zakrewski PRL (2020)

Challenging finite-size scaling
Disorder \(h\)
Disorder \(h\)
\(h/L\)
\(h\)
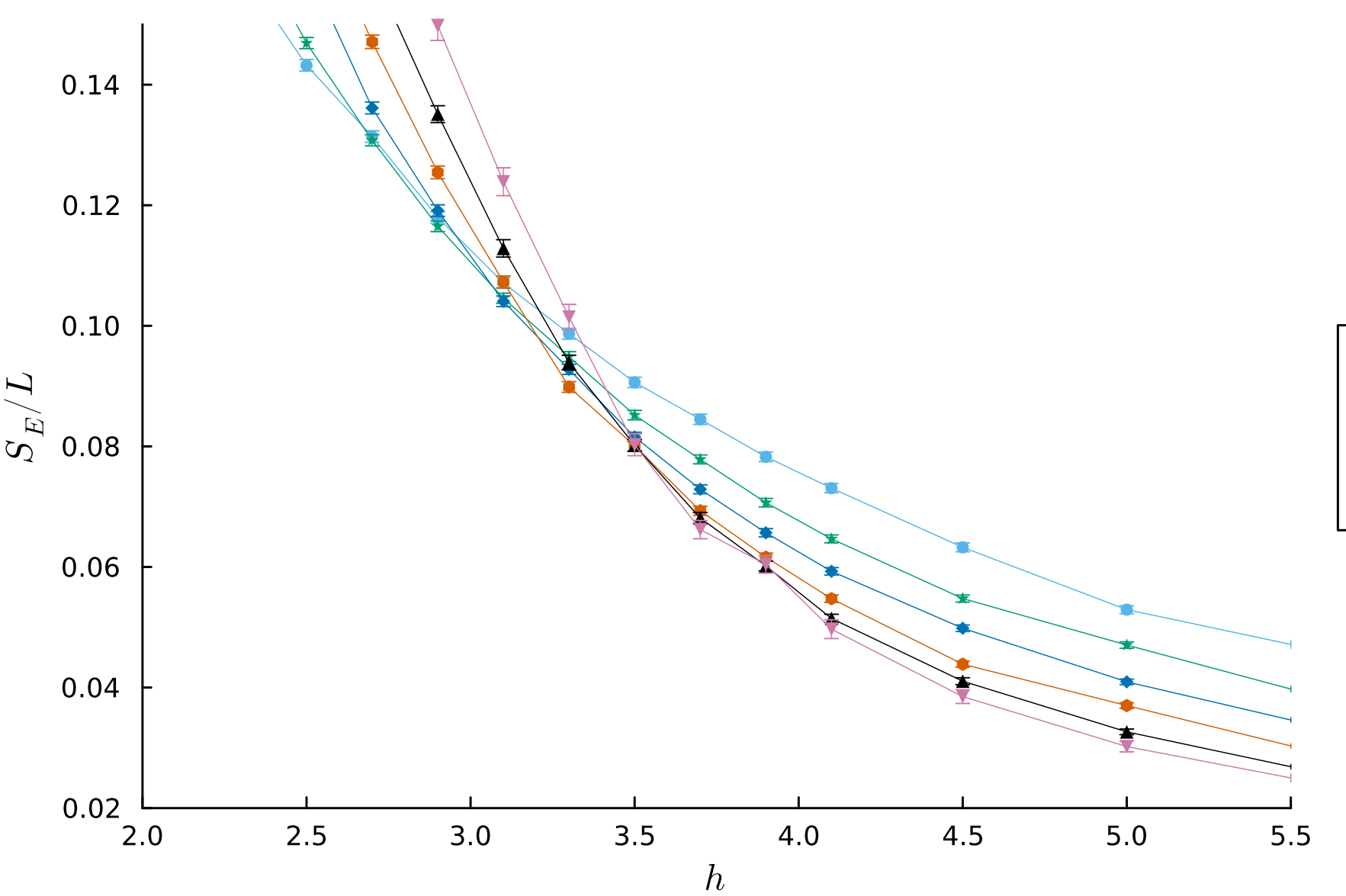
Entanglement entropy
& other probes

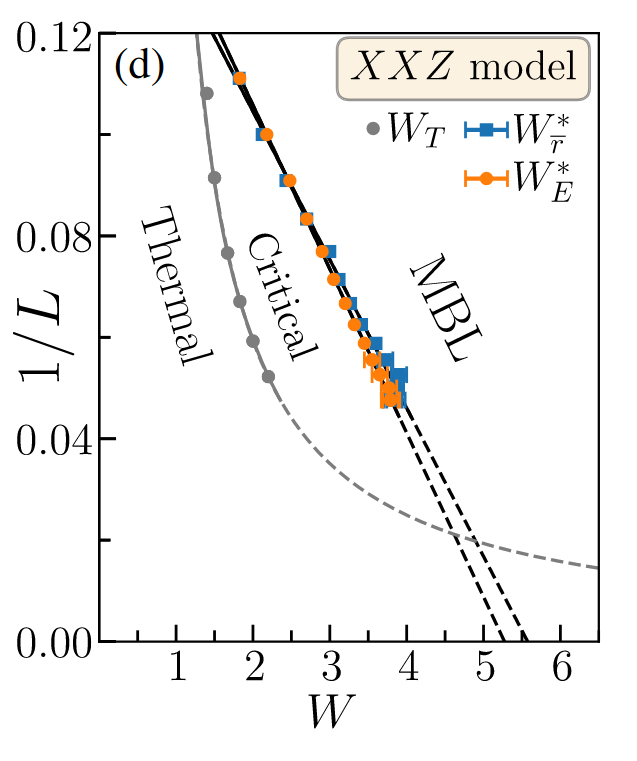
JC, F. Alet, N. Laflorencie, PRL (2024)
Suntajs et al (2020)
(arXiv v1-v2)
3
3
18
COLBOIS | FROM AL TO MBL | 07.2025
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
3
3
19
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
COLBOIS | FROM AL TO MBL | 07.2025
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Morningstar et al, PRB 105 (2022)
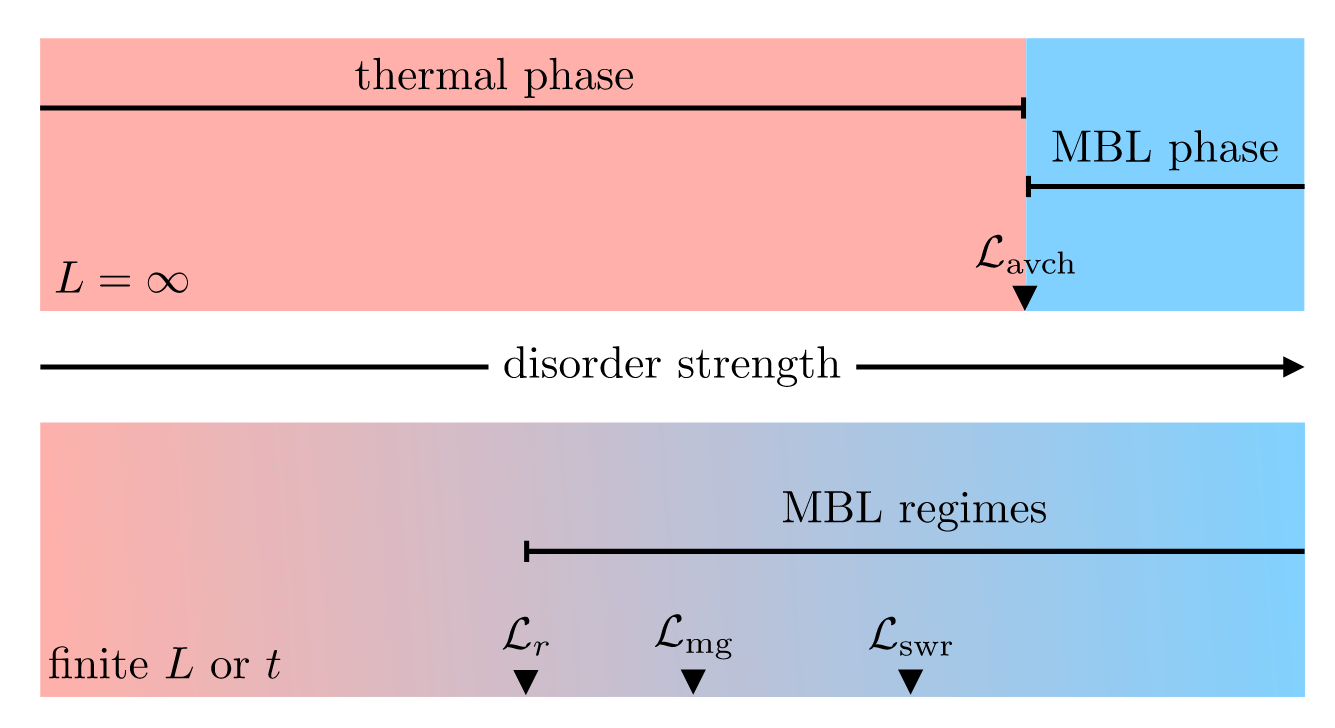
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
3
3
19
Phase diagram(s) and instabilities
COLBOIS | FROM AL TO MBL | 07.2025
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Morningstar et al, PRB 105 (2022)

avalanche instability
De Roeck & Huveneers (2017), Luitz, De Roeck & Huveneers (2017),
Thiery et al (2018); Crowley and Chandran (2020), Crowley and Chandran (2022)
Small ergodic region triggers runaway delocalization
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
3
3
19
COLBOIS | FROM AL TO MBL | 07.2025
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Morningstar et al, PRB 105 (2022)

many-body resonances
Gopalakrishnan et al (2015)
Villalonga and Clark (2020)
Garratt et al (2021)
Crowley and Chandran (2022)
Morningstar et al (2022)
MBL is destabilized by resonances between localized eigenstates finite-size crossover
avalanche instability
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
3
3
19
COLBOIS | FROM AL TO MBL | 07.2025
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
Morningstar et al, PRB 105 (2022)

avalanche instability
gap ratio
and minimum gap
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
3
3
19
many-body resonances
COLBOIS | FROM AL TO MBL | 07.2025
\(L \rightarrow \infty\)
Kiefer-Emmanouilidis et al (2020), Suntajs et al (2020), Sels, Polkovnikov (2021), Wiesse et al (2024),...
Evers et al (2023),Long (2023)...
JC, Alet, Laflorencie (2024), Laflorencie et al (2025)
Sierant et al(2020), Morningstar et al, (2022) , Crowley, Chandran (2022), Szoldra et al (2024), Nieda et al (2024), Scoquart et al (2025)....
Weiner et al (2019), Sierant, Zakrewski (2022),
Biroli et al (2024)
See Nicolas' talk for a discussion
Morningstar et al, PRB 105 (2022)

avalanche instability
3
3
8
many-body resonances
Rest of the talk :
one or Two short stories motivated by these instabilities
Absence of MBL phase
Single transition from ergodic to MBL (potentially very large \(h_c\))
Intermediate phase (nature differs depending on the paper)
h
h
h
Phase diagram(s) and instabilities
3
3
19
COLBOIS | FROM AL TO MBL | 07.2025
Avalanches
Resonances
Avalanches
Anderson localization has an ergodic instability at weak disorder
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
Resonances
Avalanches
Anderson localization has an ergodic instability at weak disorder
Resonances
We find long-range cat states deep in the MBL regime
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
JC, F. Alet, N. Laflorencie, PRB (2024)
N. Laflorencie, JC, F. Alet, arXiv (2025)
?
Anderson insulator
disorder \(h \)
Ising interaction \(\Delta\)
Ergodic
Many-body localized
?
?
?
5. An avalanche short story:
Stepping away from Strong interactions
Anderson insulator
disorder \(h \)
Ising interaction \(\Delta\)
Ergodic
Many-body localized
?
5. An avalanche short story:
Stepping away from Strong interactions
\(n_0\)
Runaway instability induced by rare regions of weak disorder
De Roeck & Huveneers (2017), Luitz, De Roeck & Huveneers (2017),
Thiery et al (2018); Crowley and Chandran (2020), Crowley and Chandran (2022)
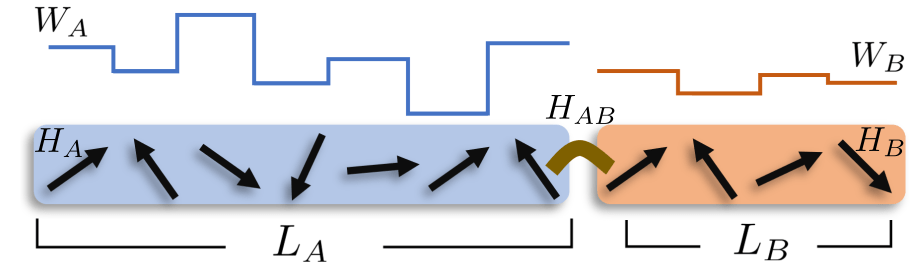
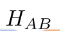
Adapted from Szoldra et at (2024)





Avalanche Argument
3
3
20
COLBOIS | FROM AL TO MBL | 07.2025
\(n_0\)
Runaway instability induced by rare regions of weak disorder
De Roeck & Huveneers (2017), Luitz, De Roeck & Huveneers (2017),
Thiery et al (2018); Crowley and Chandran (2020), Crowley and Chandran (2022)

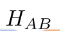
Adapted from Szoldra et at (2024)





Avalanche Argument
3
3
20
COLBOIS | FROM AL TO MBL | 07.2025
thermal "bubble" with level spacing \(\delta \sim 2^{-n_0}\)
\(n_0\)
Runaway instability induced by rare regions of weak disorder
\(\Gamma \sim e^{-r/\zeta}\)
De Roeck & Huveneers (2017), Luitz, De Roeck & Huveneers (2017),
Thiery et al (2018); Crowley and Chandran (2020), Crowley and Chandran (2022)

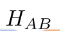
Adapted from Szoldra et at (2024)





Avalanche Argument
3
3
20
COLBOIS | FROM AL TO MBL | 07.2025
thermal "bubble" with level spacing \(\delta \sim 2^{-n_0}\)
\(n_0\)
Runaway instability induced by rare regions of weak disorder
\(\Gamma \sim e^{-r/\zeta}\)
thermal "bubble" with level spacing \(\delta \sim 2^{-n_0}\)
Spin relaxes if the interaction does not resolve the spectral gap of the grain
\(\zeta > \zeta_c\)
De Roeck & Huveneers (2017), Luitz, De Roeck & Huveneers (2017),
Thiery et al (2018); Crowley and Chandran (2020), Crowley and Chandran (2022)

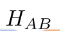
Adapted from Szoldra et at (2024)





Avalanche Argument
3
3
20
COLBOIS | FROM AL TO MBL | 07.2025
Avalanche theory At weak interactions
3
3
21
COLBOIS | FROM AL TO MBL | 07.2025
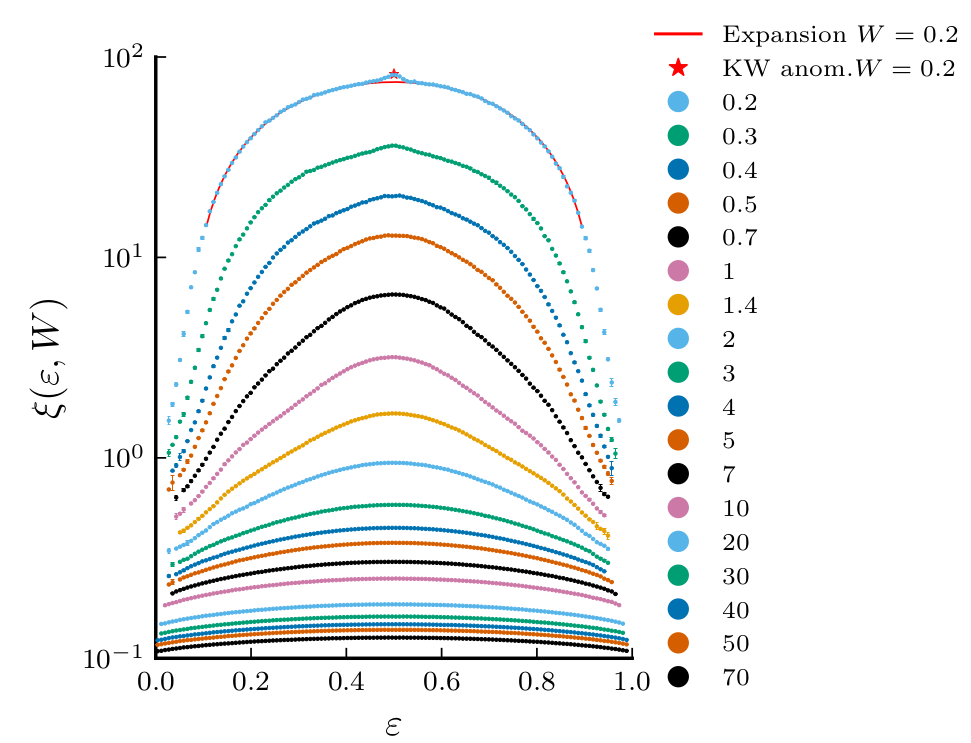
- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
Avalanche theory At weak interactions
3
3
21
COLBOIS | FROM AL TO MBL | 07.2025
- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
Avalanche theory At weak interactions
\(\epsilon\)
\(\epsilon_{\rm sp}\)
Colbois and Laflorencie (2023), Crowley and Chandran (2020)
3
3
21
COLBOIS | FROM AL TO MBL | 07.2025
- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
Avalanche theory At weak interactions

\(\epsilon\)
\(\epsilon_{\rm sp}\)
Colbois and Laflorencie (2023), Crowley and Chandran (2020)
\(h/J\)
\(h/J \gg 1 \)
\(\xi_{\mathrm{MBA}} \ll L \)
\(\Rightarrow\)
3
3
21
COLBOIS | FROM AL TO MBL | 07.2025
- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
- Localization length typically increases with \(\Delta\)
Avalanche theory At weak interactions
\(h\)

Crowley and Chandran (2020), Colbois and Laflorencie (2023)
3
3
22
COLBOIS | FROM AL TO MBL | 07.2025
Avalanche theory At weak interactions
\(h\)

- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
- Localization length typically increases with \(\Delta\)
Crowley and Chandran (2020), Colbois and Laflorencie (2023)
3
3
22
COLBOIS | FROM AL TO MBL | 07.2025
Avalanche theory At weak interactions
\(h\)

\(h^{\star}\)
- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
- Localization length typically increases with \(\Delta\)
Crowley and Chandran (2020), Colbois and Laflorencie (2023)
3
3
22
COLBOIS | FROM AL TO MBL | 07.2025
Avalanche theory At weak interactions
\(h\)

High energy, \( \epsilon = 0.5\)
Ising interaction \(\Delta\)
MBL
Delocalized
disorder \(h \)
!
\(h^{\star}\)
\(h^{\star}\)
- Any reasonable definition of \(\zeta\) should become \(\xi_{\rm MBA}\) at weak interactions
- Localization length typically increases with \(\Delta\)
Crowley and Chandran (2020), Colbois and Laflorencie (2023)
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
3
3
22
COLBOIS | FROM AL TO MBL | 07.2025
(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5; Crowley and Chandran 2020 )
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
\(\Delta/J\)
\(h/J \)

Ergodic instability of Anderson localization

3
3
23
Delocalized at strong enough interactions
COLBOIS | FROM AL TO MBL | 07.2025
(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5; Crowley and Chandran 2020 )
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
\(\Delta/J\)
\(h/J \)


Ergodic instability of Anderson localization

Delocalized at strong enough interactions
Critical interaction drifts to zero!
3
3
23
COLBOIS | FROM AL TO MBL | 07.2025
\(\Delta/J\)
\(h/J \)


Ergodic instability of Anderson localization
(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5; Crowley and Chandran 2020 )
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
3
3
23
COLBOIS | FROM AL TO MBL | 07.2025
\(\Delta/J\)
\(h/J \)


Ergodic instability of Anderson localization
(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5; Crowley and Chandran 2020 )
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
3
3
23
COLBOIS | FROM AL TO MBL | 07.2025
\(\Delta/J\)
\(h/J \)


Ergodic
MBL
Ergodic instability of Anderson localization
(See also LeBlond et al., PRB 104 L201117 (2021), @ h = 0.5; Crowley and Chandran 2020 )
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
3
3
23
COLBOIS | FROM AL TO MBL | 07.2025
6. A Correlations short story
Hunting for many-body resonances
High energy, \(\epsilon = 0.5\)
Ising interaction \(\Delta\)
MBL
Delocalized
disorder \(h \)
Instabilities : Many-body resonances
Gopalakrishnan et al (2015)
Villalonga and Clark (2020)
Garratt et al (2021)
Crowley and Chandran (2022)
Morningstar et al (2022)
3
3
24
COLBOIS | FROM AL TO MBL | 07.2025
Another possible mechanism for instabilities:
resonances between more localized many-body states
High energy, \(\epsilon = 0.5\)
Ising interaction \(\Delta\)
MBL
Delocalized
disorder \(h \)
Gopalakrishnan et al (2015)
Villalonga and Clark (2020)
Garratt et al (2021)
Crowley and Chandran (2022)
Morningstar et al (2022)
\(r\)
Instabilities : Many-body resonances
COLBOIS | FROM AL TO MBL | 07.2025
3
3
24
Another possible mechanism for instabilities:
resonances between more localized many-body states
High energy, \(\epsilon = 0.5\)
Ising interaction \(\Delta\)
MBL
Delocalized
disorder \(h \)
\(r\)
\(r\)
Gopalakrishnan et al (2015)
Villalonga and Clark (2020)
Garratt et al (2021)
Crowley and Chandran (2022)
Morningstar et al (2022)
\(\pm\)
Perturb away from very strong disorder
Instabilities : Many-body resonances
Another possible mechanism for instabilities:
resonances between more localized many-body states
COLBOIS | FROM AL TO MBL | 07.2025
3
3
24
High energy, \(\epsilon = 0.5\)
Ising interaction \(\Delta\)
MBL
Delocalized
disorder \(h \)
\(r\)
\(r\)
Gopalakrishnan et al (2015)
Villalonga and Clark (2020)
Garratt et al (2021)
Crowley and Chandran (2022)
Morningstar et al (2022)
\(\pm\)
Perturb away from very strong disorder
Instabilities : Many-body resonances
Another possible mechanism for instabilities:
resonances between more localized many-body states
COLBOIS | FROM AL TO MBL | 07.2025
3
3
24
Hints in several works but extremely challenging to characterize
Jacobi method
Demixing
QMI
Fictitious evolution
Phenomenological models
Relation to avalanches
Kjäll (2018)
Colmenarez et al (2019)
Villalonga and Clark (2020)
Crowley and Chandran (2020)
Garatt et al (2021)
Crowley and Chandran (2022)
Long et al (2023)
Ha, Morningstar and Huse (2023)
Morningstar et al (2022)
Gopalakrishnan et al (2015)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L\)
- used with QMI
- risk of edge effects?
Morningstar et al (2022)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L\)
- used with QMI
- risk of edge effects?
Morningstar et al (2022)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L\)
- used with QMI
- risk of edge effects?
Morningstar et al (2022)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
see e.g. Varma et al., PRB (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L\)
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
- used with QMI
- risk of edge effects?
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Morningstar et al (2022)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L\)
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
- used with QMI
- risk of edge effects?
Morningstar et al (2022)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Mid-chain correlations
Distance-dependent \(|C^{\alpha\alpha}_r|\) :
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L\)
Systemwide \(|C^{\alpha\alpha}_r|\) : \(r = L/2\)
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
- used with QMI
- risk of edge effects?
Morningstar et al (2022)
- no \(r\)-dep. in the ergodic phase \(\epsilon = 0.5\)
- inherent difficulties with PBC
COLBOIS | FROM AL TO MBL | 07.2025
3
3
25
see e.g.
Pal & Huse (2010)
Varma et al. (2019)
Villalonga and Clark (2020)
Colmenarez et al (2019)
Spin-Spin Correlations
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
Simple, experimentally accessible, somewhat overlooked
Two simple limits
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
26
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

- bulk decay matches mid-chain decay
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(h = 5\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
26
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

- bulk decay matches mid-chain decay
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
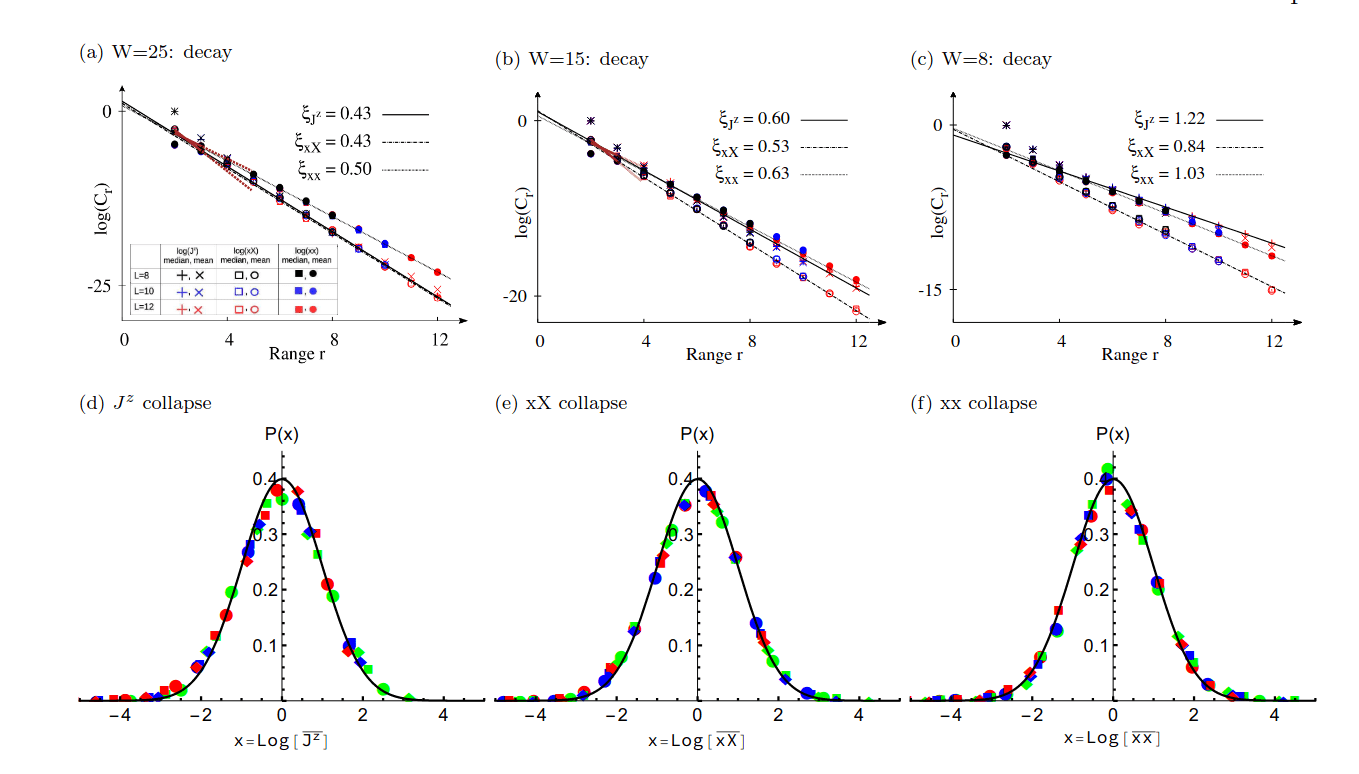
\(\xi^z_{\mathrm{bulk}} = 0.448 \pm 0.005\)
\(\xi^z_{\mathrm{mid}} = 0.449 \pm 0.003\)
\(\xi^x_{\mathrm{bulk}} = 0.87 \pm 0.01\)
\(\xi^x_{\mathrm{mid}} = 0.89 \pm 0.01\)
\(h = 5\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
26
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
26
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
26
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate
Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
ONLY SIZE DEPENDENCE!
No spatial dependence,
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
Total spin conservation
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
ONLY SIZE DEPENDENCE!
No spatial dependence,
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
Total spin conservation
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
Power-law
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
Total spin conservation
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
Power-law
Random state : XX
\(\bra{R} S_i^{+} S_j^{-} \ket{R}\)
\(= \sum_{s} a_s a_{\mathrm{flip}(s)}\) \(\propto \frac{ \sqrt{\mathcal{N}}}{\mathcal{N}}\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
Total spin conservation
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
finite \(\xi_x\)
Power-law
Random state : XX
\(\bra{R} S_i^{+} S_j^{-} \ket{R}\)
\(= \sum_{s} a_s a_{\mathrm{flip}(s)}\) \(\propto \frac{ \sqrt{\mathcal{N}}}{\mathcal{N}}\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate


Random vector
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
Total spin conservation
Random state : XX
\(\ket{R} = \sum_{s= 1}^{\mathcal{N}} a_s \ket{s}\), \(\ket{s} = \ket{\uparrow, \downarrow, \dots}\),\( |a_s|^2\propto\frac{1}{\mathcal{N}}\)
finite \(\xi_x\)
Power-law
ZZ correlations dominate
\(\bra{R} S_i^{+} S_j^{-} \ket{R}\)
\(= \sum_{s} a_s a_{\mathrm{flip}(s)}\) \(\propto \frac{ \sqrt{\mathcal{N}}}{\mathcal{N}}\)
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Ergodic typical eigenstate = random vector
Anderson localized \(\Delta = 0\)

\(\xi_x \approx 2 \xi_z\) : XX correlations dominate
ZZ correlations dominate



Random vector
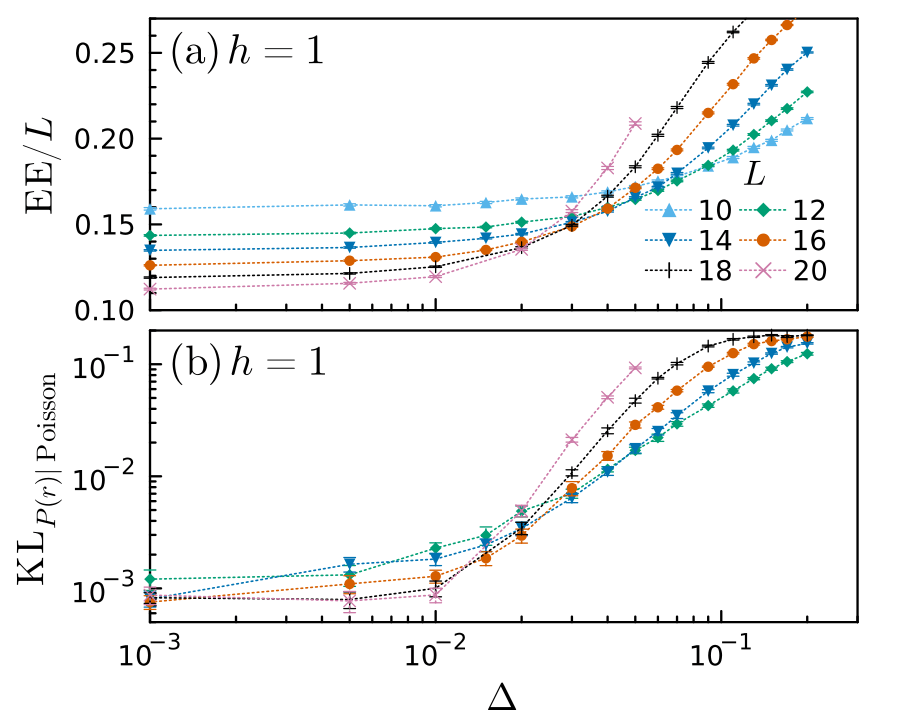
XXZ, \(h = 1, \Delta = 1\)
finite \(\xi_x\)
- bulk decay matches mid-chain decay
- good proxy for the localization length
Two simple limits
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
\(C_{r}^{\alpha\alpha} = \langle S_i^{\alpha} S_{i+r}^{\alpha} \rangle - \langle S_i^{\alpha} \rangle \langle S_{i+r}^{\alpha} \rangle\)
\(\xi_{\mathrm{MBA}}\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
27
Random vector
finite \(\xi_x\)
Inversion of the dominant correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
28
JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Inversion of the dominant correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
28

JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
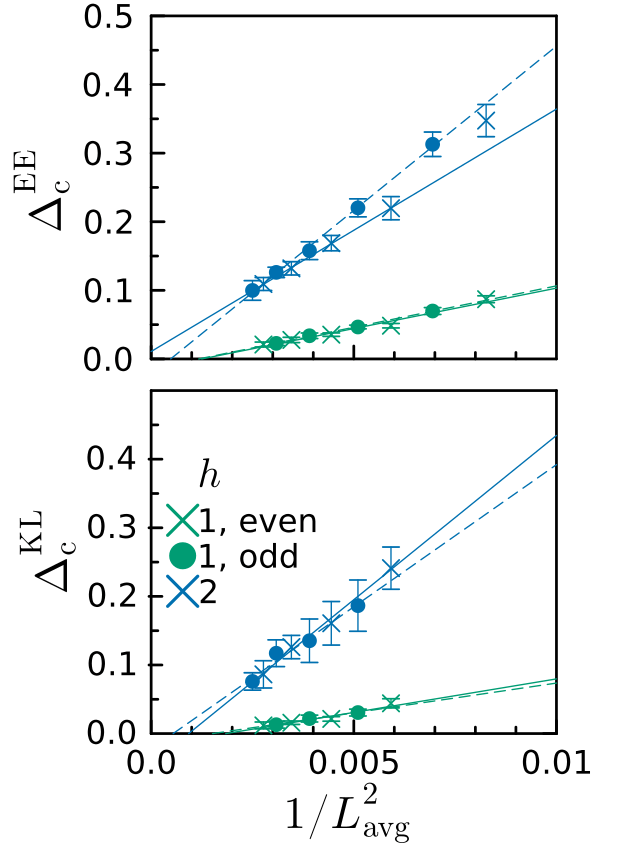
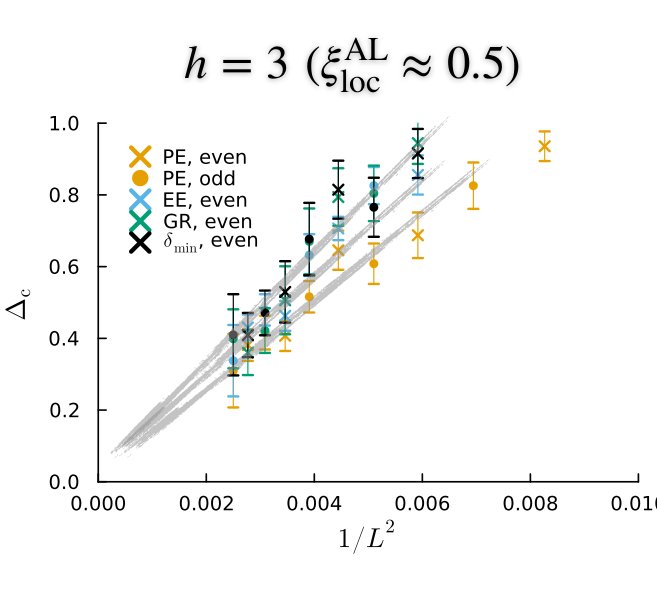
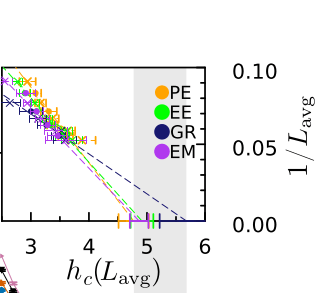
Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
Inversion of the dominant correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
28

JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
Inversion of the dominant correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
28

JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
An inversion of the dominant correlations occurs deeper in the MBL regime
Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
Inversion of the dominant correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
28

JC, F. Alet, N. Laflorencie, PRL 133 and PRB 110, (2024)
Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
An inversion of the dominant correlations occurs deeper in the MBL regime
Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
?
Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

XX
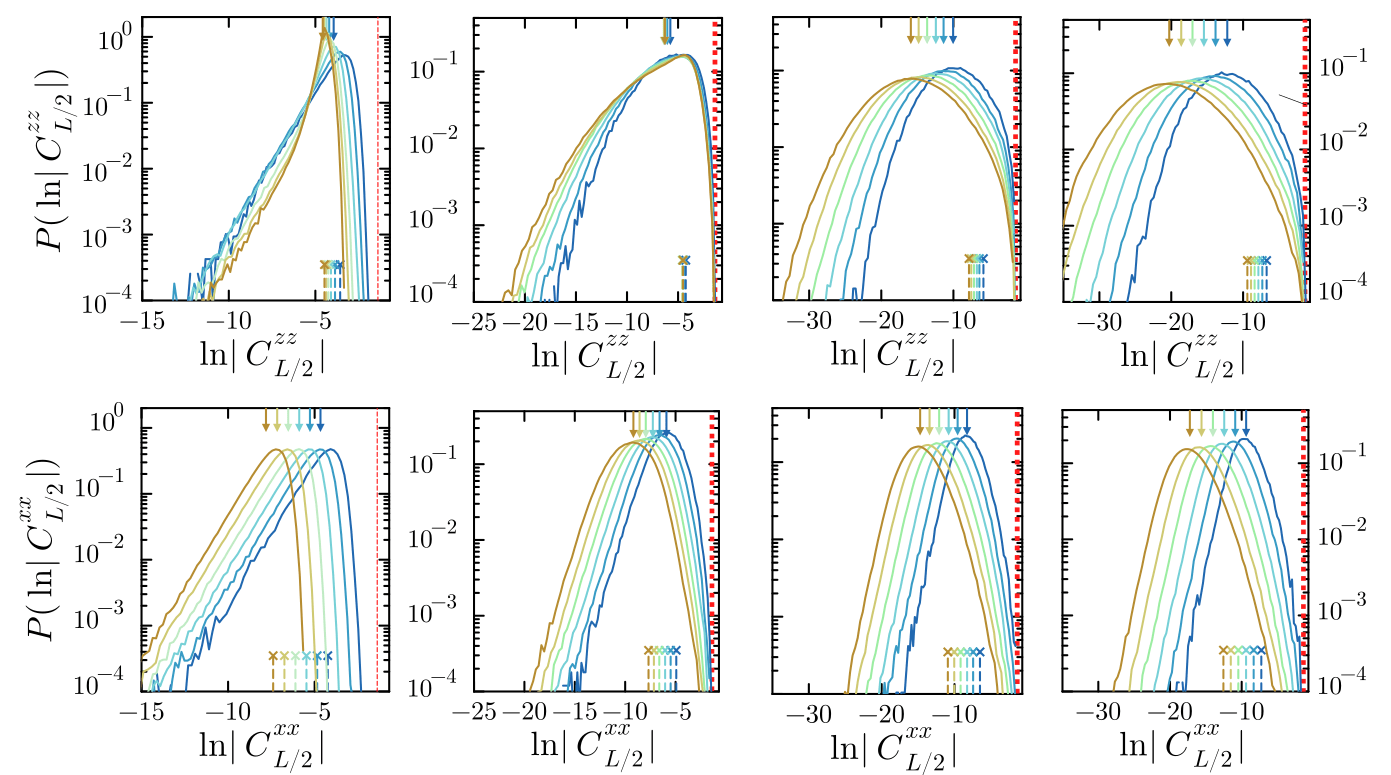
Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

XX

Limited broadening with \(L\)
Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

XX

Limited broadening with \(L\)
Limited weight at large correlations
Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

XX
ZZ

Limited broadening with \(L\)
Limited weight at large correlations
Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

XX
ZZ

Limited broadening with \(L\)
Limited weight at large correlations
Broadening with \(L\)
Large correlations along the Heisenberg line
COLBOIS | FROM AL TO MBL | 07.2025
3
3
29
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

XX
ZZ

Limited broadening with \(L\)
Limited weight at large correlations
Broadening with \(L\)
Non-zero probability of large correlations
Three questions for large correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
30
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

ZZ

Broadening with \(L\)
Non-zero probability of large correlations
Three questions for large correlations
COLBOIS | FROM AL TO MBL | 07.2025
3
3
30

ZZ

Broadening with \(L\)
Non-zero probability of large correlations
1. Do these rare, large, long-distance correlations matter ?
2. How deep in the MBL phase can we find large correlations ?
3. What are these events ?
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)
1. Do these large correlations matter ?
COLBOIS | INSTABILITIES AND MBL | 05.2025
3
3
31
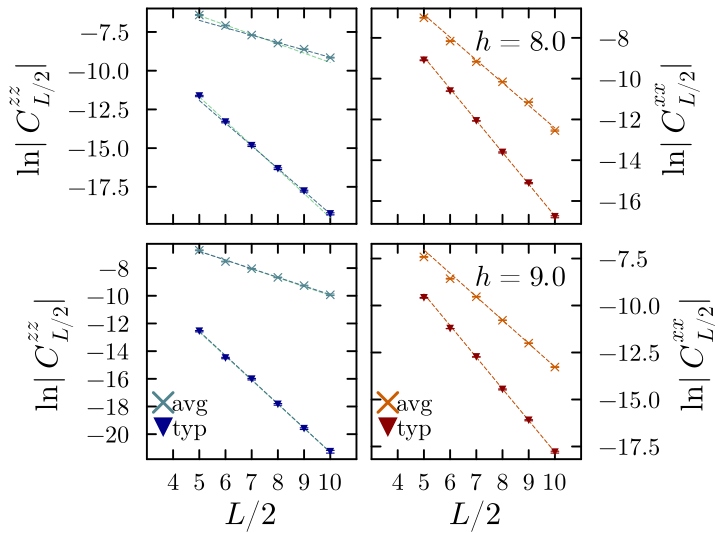
Typical vs average correlations:
Full analysis of correlations statistics: JC, F. Alet, N. Laflorencie, PRB 110, (2024)
\(\exp(\overline{\ln|C^{zz}_{L/2}|})\)
1. Do these large correlations matter ?
COLBOIS | INSTABILITIES AND MBL | 05.2025
3
3
31

Full analysis of correlations statistics: JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Typical vs average correlations:
\(\exp(\overline{\ln|C^{zz}_{L/2}|})\)
1. Do these large correlations matter ?
COLBOIS | INSTABILITIES AND MBL | 05.2025
3
3
31


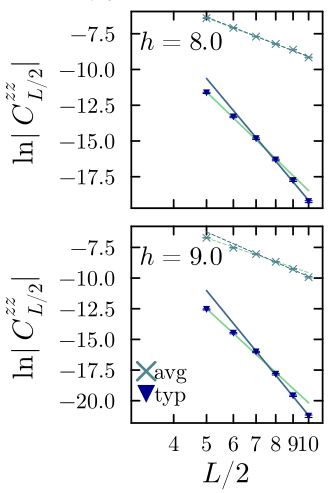

Average : better described by a power-law decay
Full analysis of correlations statistics: JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Typical vs average correlations:
\(\exp(\overline{\ln|C^{zz}_{L/2}|})\)
1. Do these large correlations matter ?
COLBOIS | INSTABILITIES AND MBL | 05.2025
3
3
31




Typical : better described by an exponential decay
Average : better described by a power-law decay
Full analysis of correlations statistics: JC, F. Alet, N. Laflorencie, PRB 110, (2024)
Typical vs average correlations:
\(\exp(\overline{\ln|C^{zz}_{L/2}|})\)
2. How deep can we find large correlationS ?
COLBOIS | FROM AL TO MBL | 07.2025
3
3
32
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)
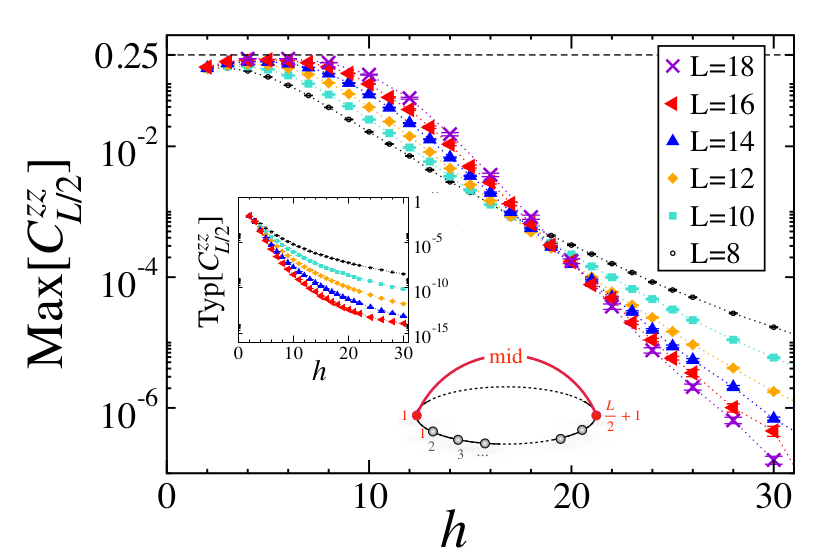
Average of the maximum over all eigenstates
2. How deep can we find large correlationS ?
COLBOIS | FROM AL TO MBL | 07.2025
3
3
32
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

Average of the maximum over all eigenstates
Up to \(h \sim 20-25\)
3. Long-distance cat states
COLBOIS | FROM AL TO MBL | 07.2025
3
3
33
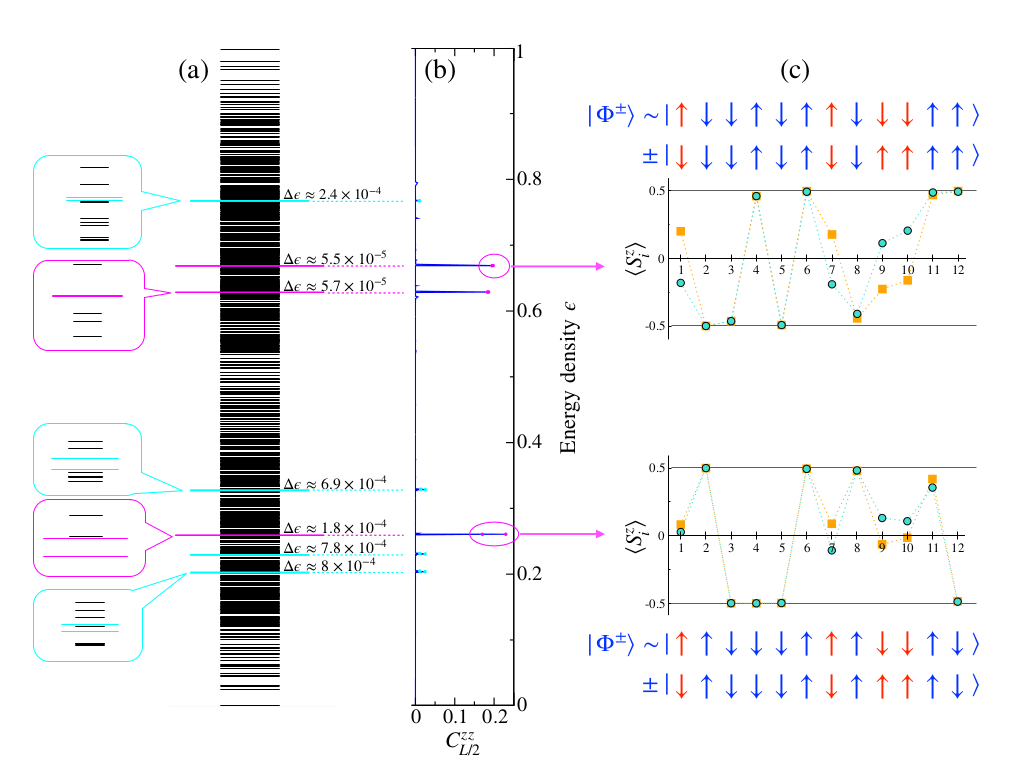
\(L = 20, h = 12\)
COLBOIS | FROM AL TO MBL | 07.2025
3
3
33

\(L = 20, h = 12\)
- Large correlations : pairs
- Extremely small gap
3. Long-distance cat states
COLBOIS | FROM AL TO MBL | 07.2025
3
3
33

\(L = 20, h = 12\)
- Large correlations : pairs
- Extremely small gap
- Cat state picture

3. Long-distance cat states
COLBOIS | FROM AL TO MBL | 07.2025
3
3
33

\(L = 20, h = 12\)
Rigorous analysis of cat states through toy model: N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)

- Large correlations : pairs
- Extremely small gap
- Cat state picture
3. Long-distance cat states
Status and Outlook
COLBOIS | FROM AL TO MBL | 07.2025
3
3
34

Diagram of the correlations regimes:
Status and Outlook
COLBOIS | FROM AL TO MBL | 07.2025
3
3
34

Diagram of the correlations regimes:
Standard observables
Status and Outlook
COLBOIS | FROM AL TO MBL | 07.2025
3
3
34

Diagram of the correlations regimes:
Average: power-law
Standard observables
Status and Outlook
COLBOIS | FROM AL TO MBL | 07.2025
3
3
34

Diagram of the correlations regimes:
Average: power-law
Average: exponential
Standard observables
Fate of this region ?
Ergodic?
Non-ergodic delocalized?
MBL?
Status and Outlook
COLBOIS | FROM AL TO MBL | 07.2025
3
3
34
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv:2504.10566 (2025)
Pawlik et al (2025) in a Quantum Sun Model
(Others closer to the transition)

Diagram of the correlations regimes:
Rare events' importance in the MBL debate
Rare thermal regions
Rare paths in Hilbert space
Rare large correlations
Average: power-law
Average: exponential
Biroli, Hartmann, Tarzia (2024), ....
De Roeck, Huveneers (2017), Crowley, Chandran (2020),...
Rare, highly localized regions
De Roeck et al (2024), Dupont et al (2019), ...
Take-Home messages
COLBOIS | INSTABILITIES AND MBL | 05.2025
3
3
35
"Beyond the Superconducting Super Collider story:"
Anderson localization
In Anderson localization (1D, half-filling) all states are "like" ground states

COLBOIS | INSTABILITIES AND MBL | 05.2025
Take-home messages
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
3
3
36

1) Ergodic instability
Below \(h^{\star} \sim 2-3\), the Anderson insulator immediately turns ergodic for \(\Delta > 0\)
COLBOIS | INSTABILITIES AND MBL | 05.2025
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
Take-home messages
3
3
36

1) Ergodic instability
Below \(h^{\star} \sim 2-3\), the Anderson insulator immediately turns ergodic for \(\Delta > 0\)
COLBOIS | INSTABILITIES AND MBL | 05.2025
- /!\ We cannot say that our results validate avalanche theory (there could be other mechanisms)
- Finite-size effects work "in our favor"!
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
Take-home messages
3
3
36

1) Ergodic instability
Below \(h^{\star} \sim 2-3\), the Anderson insulator immediately turns ergodic for \(\Delta > 0\)
COLBOIS | INSTABILITIES AND MBL | 05.2025
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
2) Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
Take-home messages
3
3
36

3) Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
1) Ergodic instability
Below \(h^{\star} \sim 2-3\), the Anderson insulator immediately turns ergodic for \(\Delta > 0\)
COLBOIS | INSTABILITIES AND MBL | 05.2025
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
2) Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
Take-home messages
3
3
36

1) Ergodic instability
Below \(h^{\star} \sim 2-3\), the Anderson insulator immediately turns ergodic for \(\Delta > 0\)
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv (2025)
3) Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
COLBOIS | INSTABILITIES AND MBL | 05.2025
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
2) Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
Take-home messages
4) Fate of this intermediate MBL regime ?
Driven by rare cat states?
3
3
36

1) Ergodic instability
Below \(h^{\star} \sim 2-3\), the Anderson insulator immediately turns ergodic for \(\Delta > 0\)
2) Extrapolated transition
Standard estimates lead to an extrapolated transition line \(h_c(\Delta)\)
3) Deep MBL
MBL and AL are connected from the point of view of correlations \(\xi_z, \xi_x\) at weak interactions
COLBOIS | INSTABILITIES AND MBL | 05.2025
Thank you !
JC, F. Alet, N. Laflorencie, PRB 110, (2024)
N. Laflorencie, JC, F. Alet, arXiv (2025)
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
Take-home messages
4) Fate of this intermediate MBL regime ?
Driven by cat states?
3
3
36
Critical interactions
Delocalized at strong enough interactions
Entanglement entropy
Spectral statistics

Critical interactions scaling
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
Correlations
\(\xi_x > \xi_z\)
Inversion
Extrapolated \(h_c\)
\(\xi_z \rightarrow \infty\)



Heisenberg line
Ergodic
Ergodic
Ergodic
Vertical cut
\(h/J \)


Ergodic
MBL
\(h/J \)


Ergodic
MBL
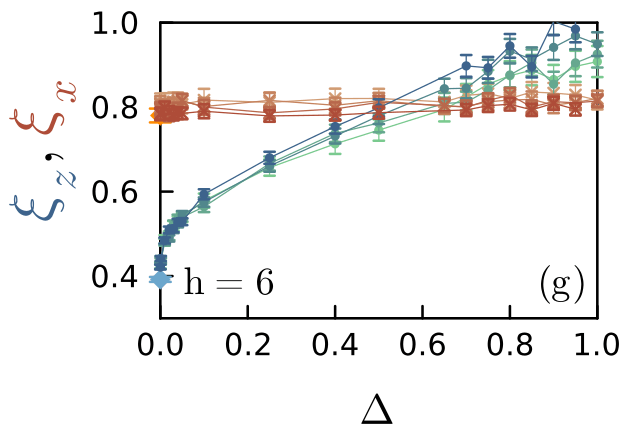
- \(\xi_{z,x}\) very short
- Directly connected to AL values
- Flat \(\xi_x\), fast increase of \(\xi_z\)
- Instability
Ergodic
JC, F. Alet, N. Laflorencie, PRL 133, 116502 (2024)
Dynamics
Dynamics
Anderson
No growth
of entanglement

J. H. Bardarson, F. Pollmann, and J. E. Moore, PRL 109, 017202 (2012)
M. Znidaric, T. Prosen, and P. Prelovsek PRB 77, 064426 (2008)
Log growth
of entanglement
Initial \(S^z\) basis random product state
+
TEBD
W = 5

D. Luitz, N. Laflorencie, F. Alet (2016)
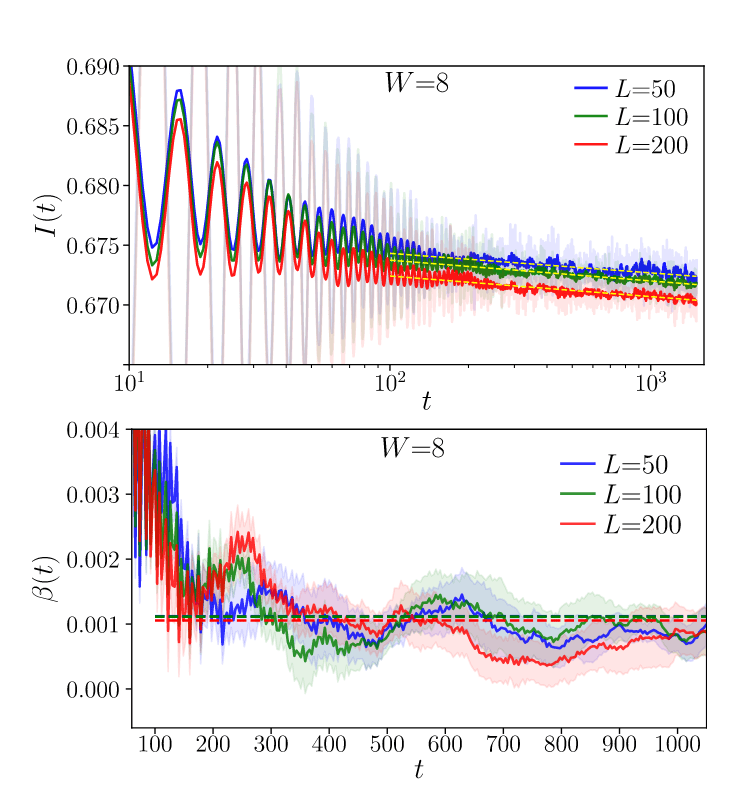
Sierant and Zakrewski (2022)
Other probes
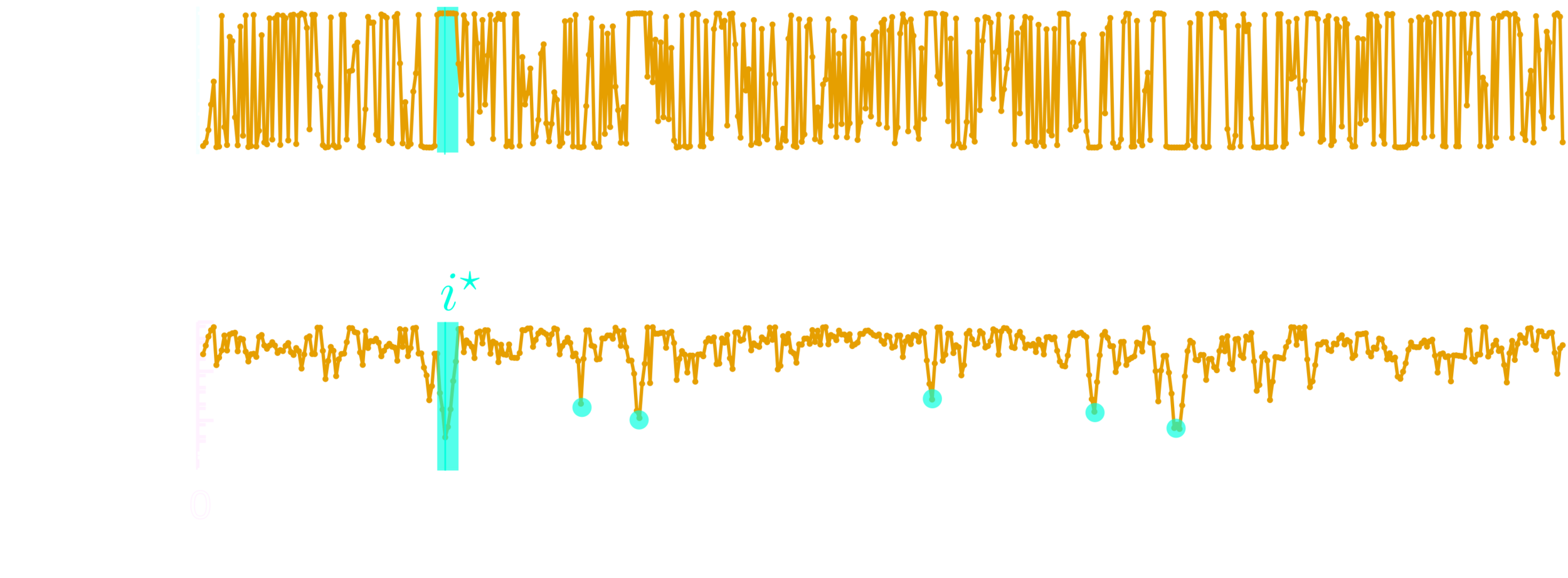
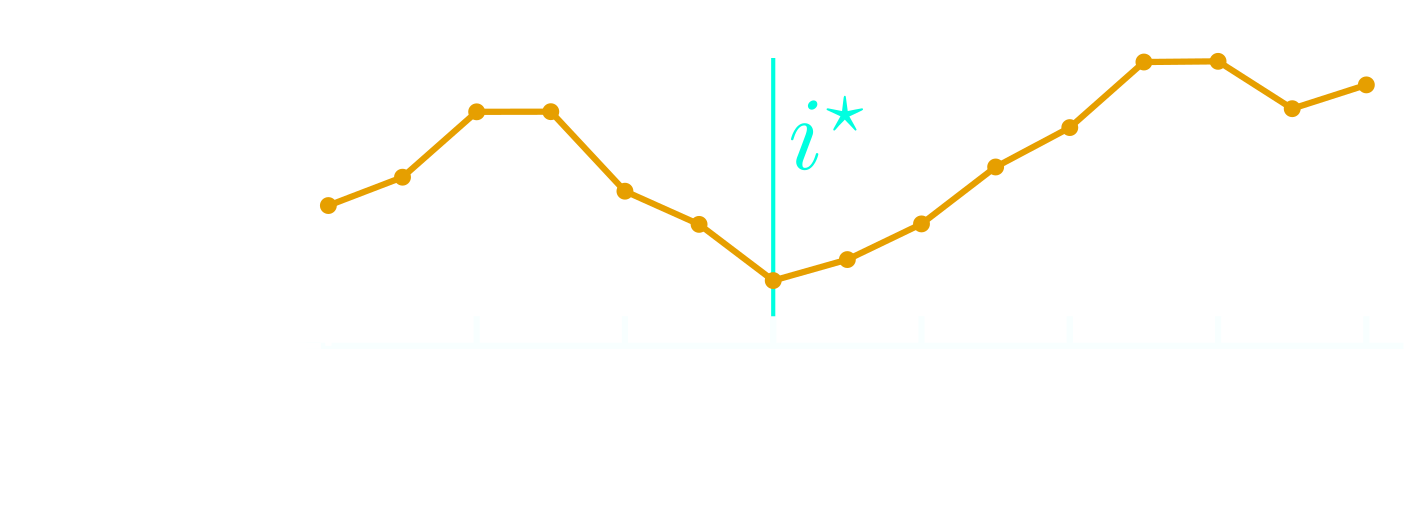
Some eigenstate
J. C., N. Laflorencie, PRB (2023)
\(|\langle S_i^{z}\rangle| < 1/2\)
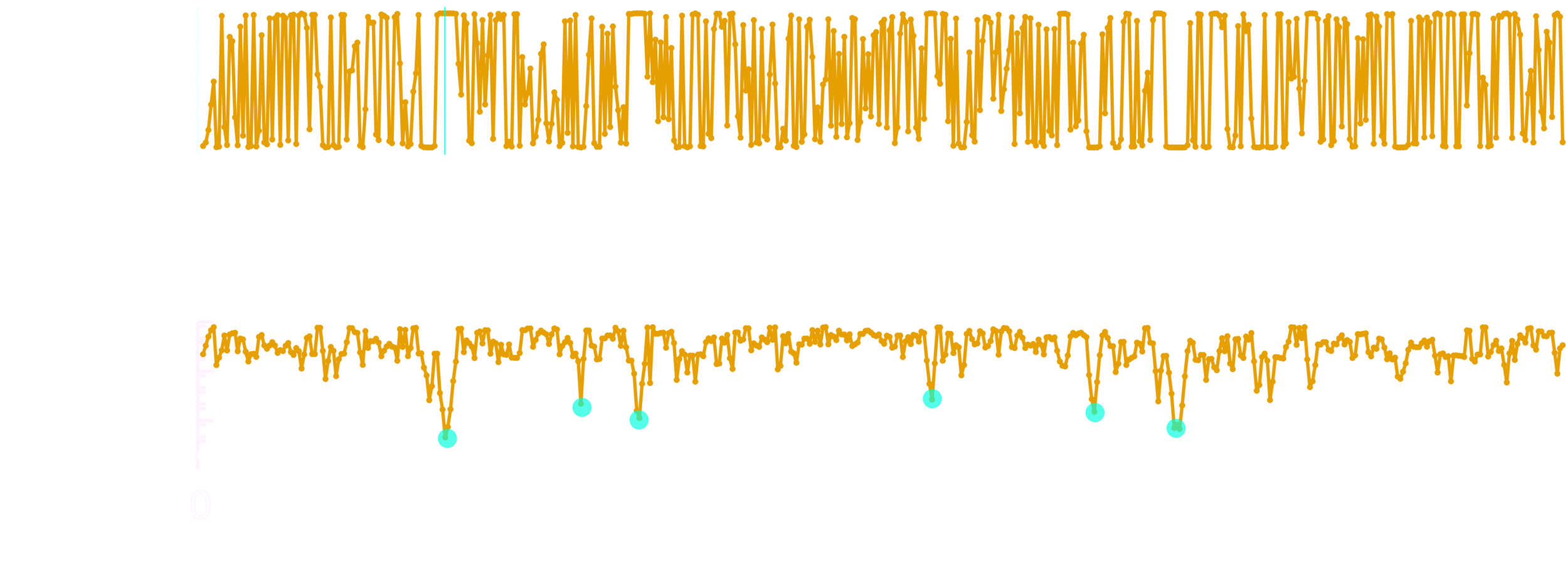
A simple many-body effect : Maximal magnetization?
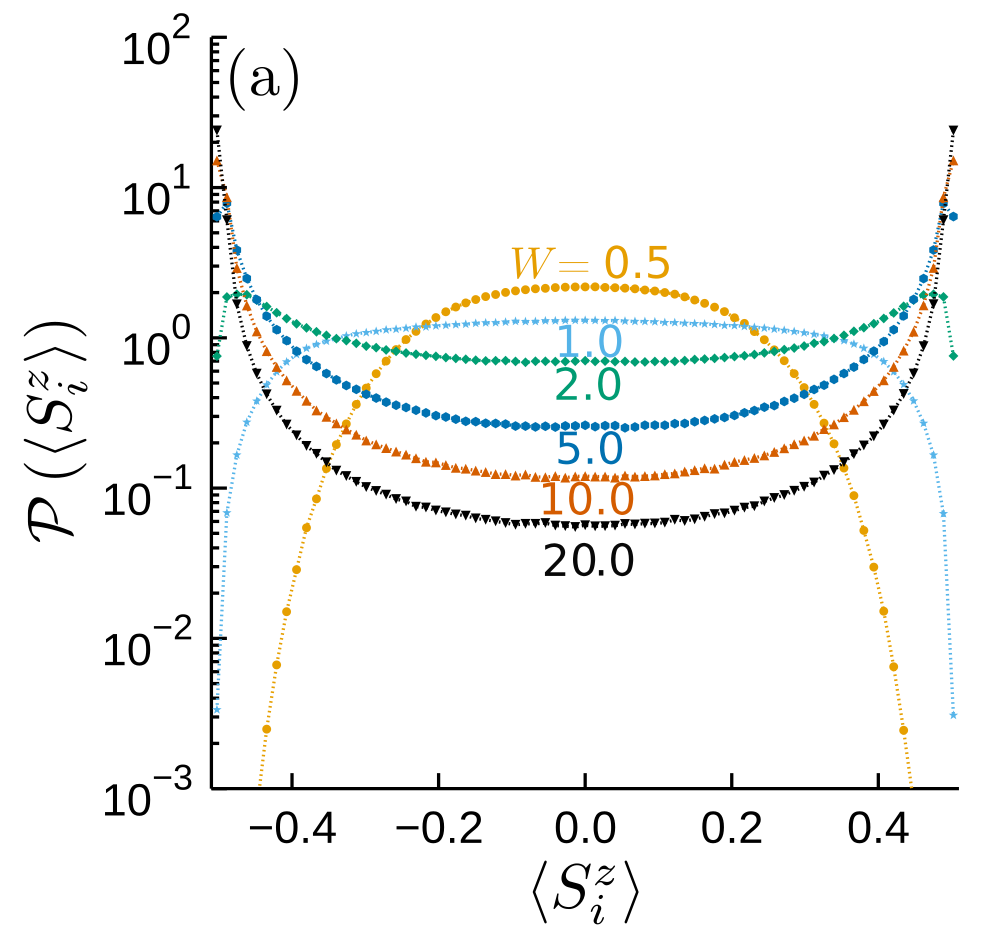
Anderson chain / XX chain
Chain breaking
Dupont, Macé, Laflorencie, PRB 100, 134201, (2019)
Laflorencie, Lemarié, Macé, PRR 2, 042033(R), (2020)
JC, Laflorencie, PRB 108, 144206 (2023)
Toy model:
SPIN FREEZING !

CHAIN BREAKING !

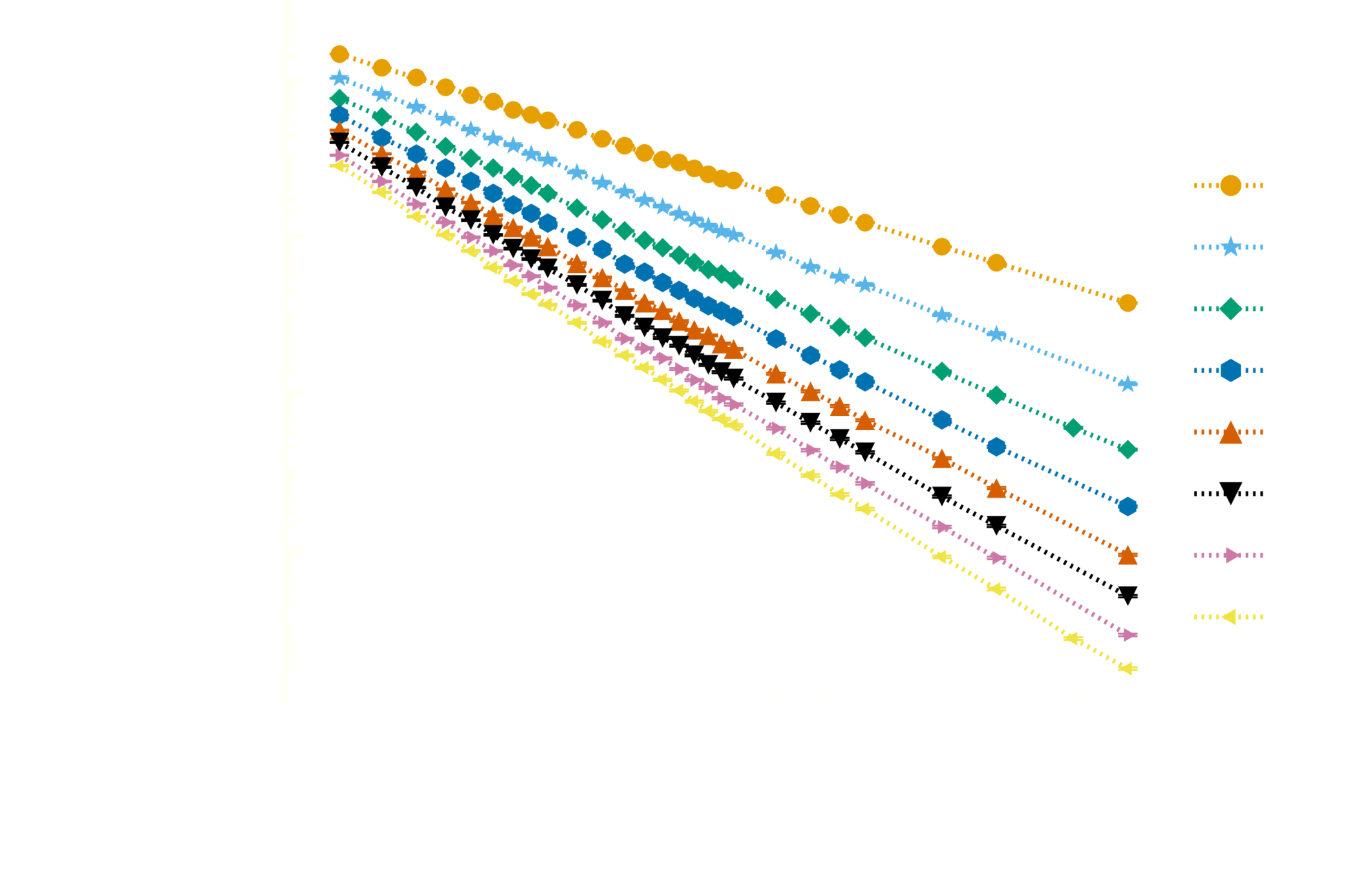
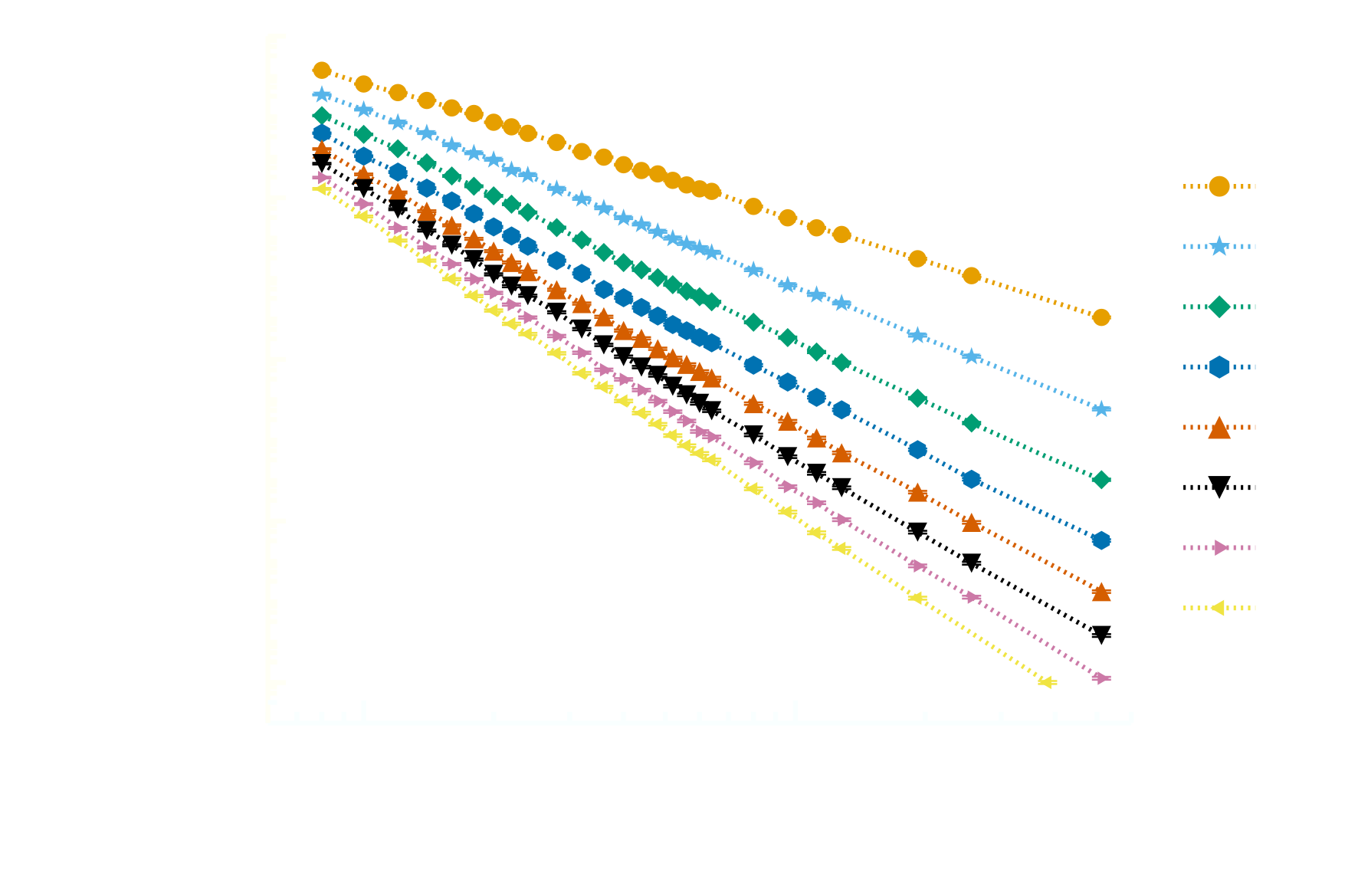
Participation entropy
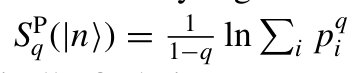
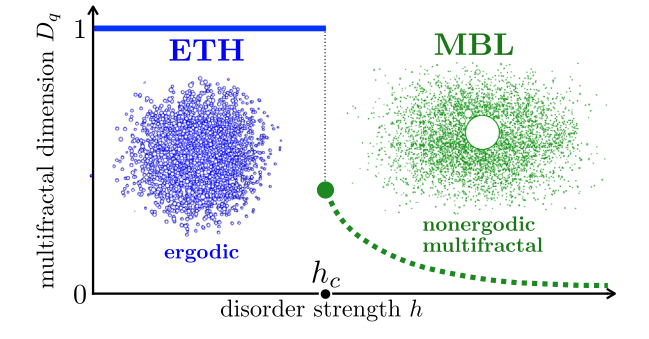
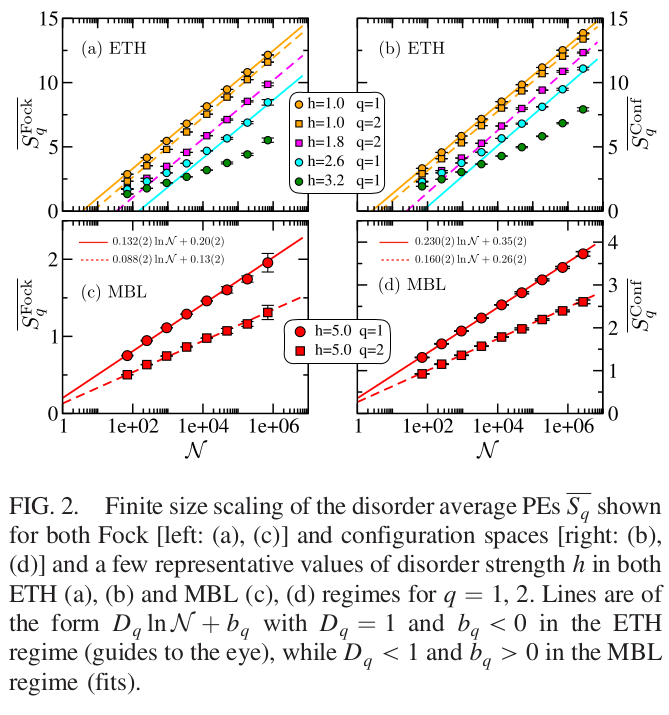
Luitz et al (2015)
Macé et al (2019)
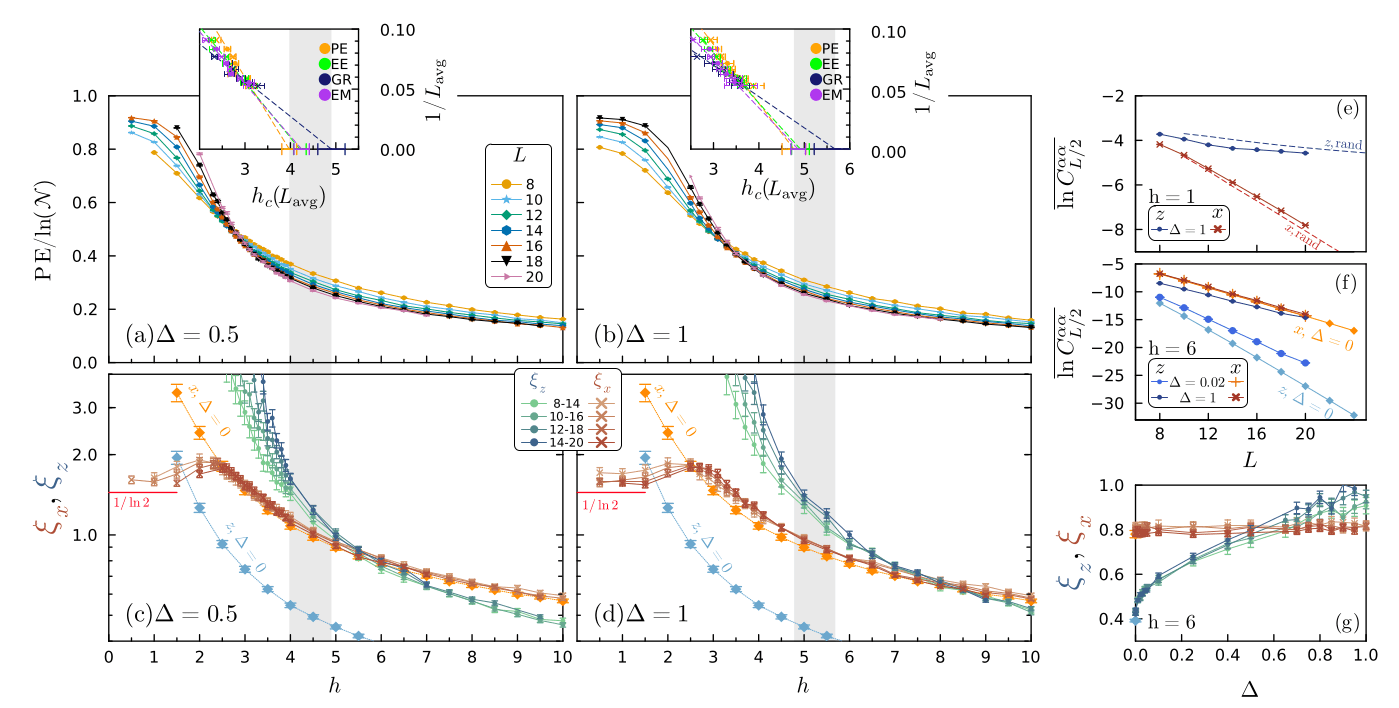
Colbois, Alet, Laflorencie (2024)
Participation entropy
Phenomenology, theory and challenges
De Roeck & Huveneers 2017, Luitz, De Roeck & Huveneers 2017, Thiery et al 2018; Crowley and Chandran 2020
Condition for spin at \(r\) to relax thanks to the grain:
Avalanche criterion:
Instabilities : Avalanches
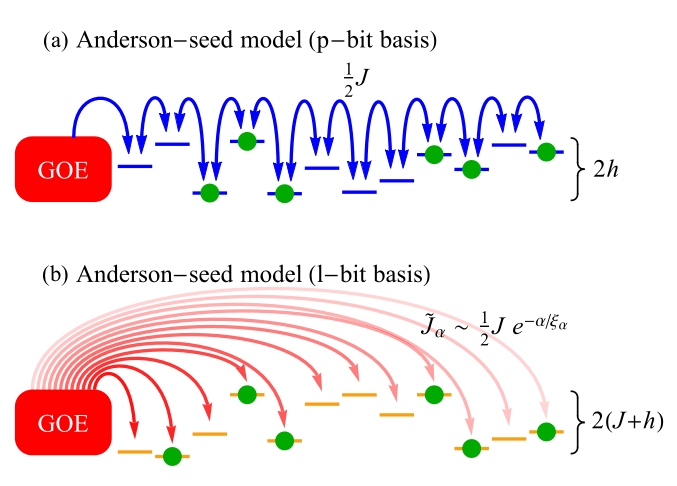
Question:
Does the seed hybridize (absorb) the l-bits?
Answer: it depends on
(1) \(V_{ij}\) the matrix element coupling the seed to the l-bit
(2) \(1/ \rho\) the level spacing.
Typically \(V_{ij} \gg 1/\rho\).
The challenge is to quantify this, see Crowley and Chandran.
L-bits models
- quasi-local integrals of motion
- In spin models : dressed physical on-site Pauli spin operators
- in fermionic models : Anderson orbitals dressed by local electron-hole excitations
- "dressed" = quasilocal, finite-depth, unitary transformation (ideally, that diagonalizes H).
- MODEL : instead of finding U, H', we define U (finite-depth circuit of 2-site gates) and H'
DEEP MBL :
- strong overlap with physical dofs -> constants of motion

- investigate to what extent the growth of number entropy can be explained directly whithin the phenomenology of MBL
- directly work with an effecting l-bits model:
- expontentially decaying support
- exponentially decaying interactions
- is particle transport entirely absent in an l-bit model ?
- ultra-slow growth, saturating in finite systems at a subextensive value increasing with system size
Landmarks
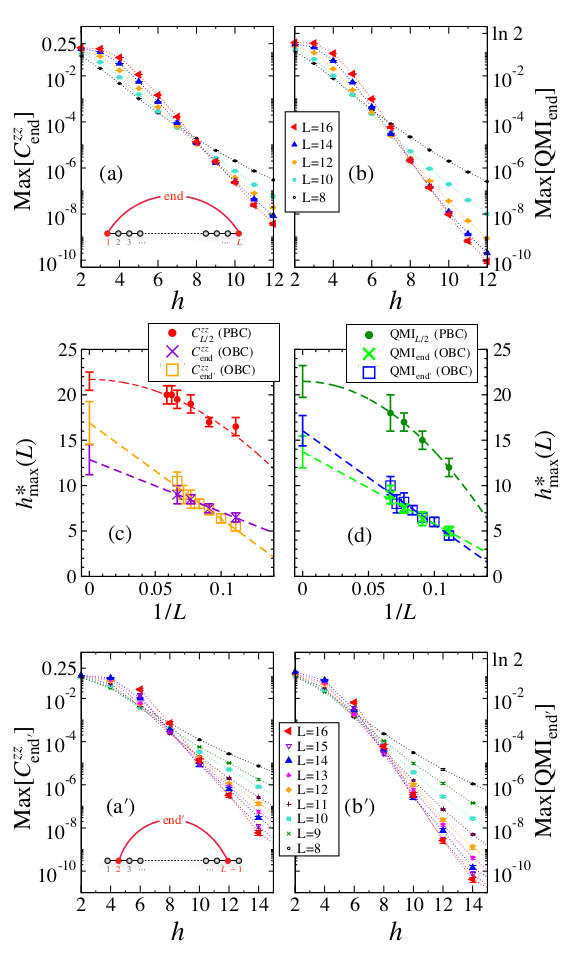


Instability at weak interactions

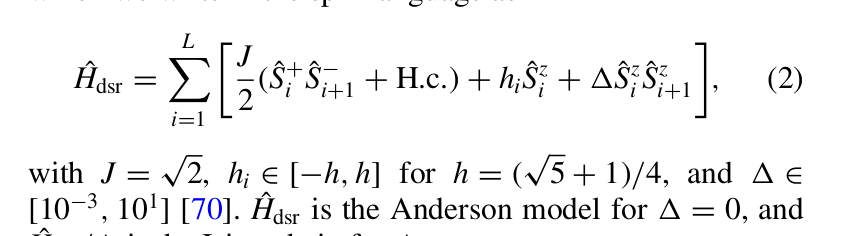

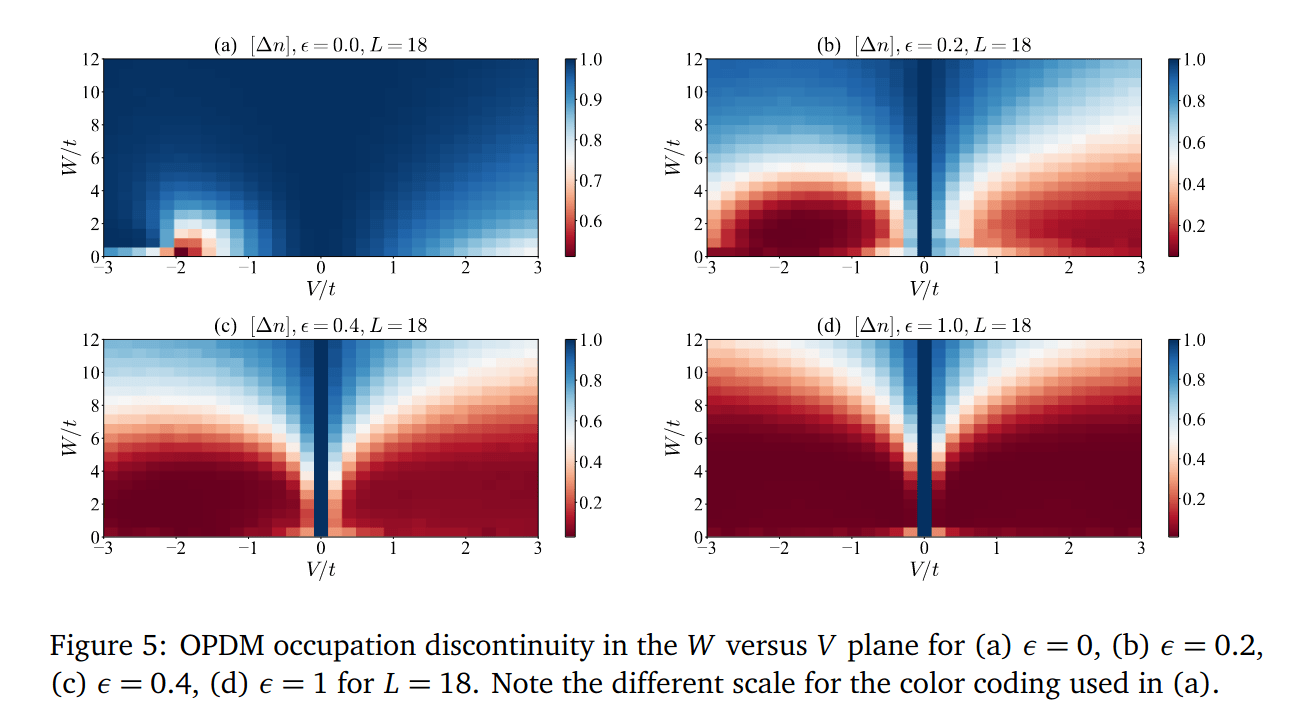


Other spatial correlations results
COLBOIS | INSTABILITIES AND MBL | 05.2025

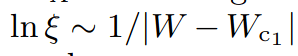
Model : t-V with usual XXZ units, except V = 2t
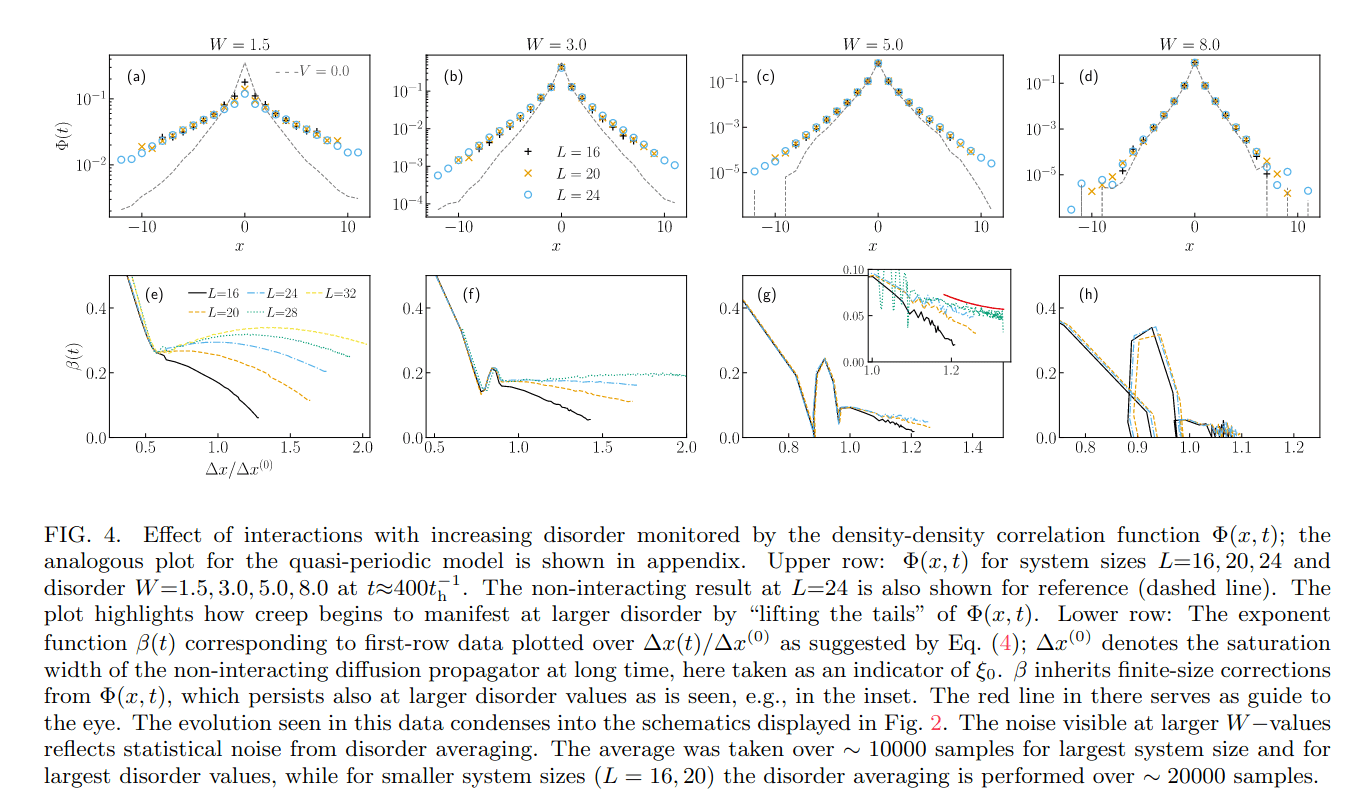
COLBOIS | INSTABILITIES AND MBL | 05.2025