Uncertainty and Risk

Christopher Makler

Stanford University Department of Economics

Econ 50: Lecture 12

pollev.com/chrismakler

What color shirt am I wearing?

pollev.com/chrismakler

Which would you choose?

$600,000 for sure

An equal chance of $200,000 or $1,000,000

pollev.com/chrismakler

Which would you choose?

DEAL: $561,000 for sure

NO DEAL: An equal chance of $200,000 or $1,000,000

Uncertainty and Risk

Lecture 12

Up to now: no uncertainty about what is going to happen in the world.

In the real world: lots of uncertainty!

We'll model this by thinking about preferences over consumption lotteries in which you consume different amounts in different states of the world.

We're just going to think about preferences, not budget constraints.

Approach

Today: Preferences over Risk

Friday: Market Implications

[worked example]

Lotteries

Expected Utility

Certainty Equivalence and Risk Premium

Insurance

Risky Assets

(Plus, some more things on intertemporal choice)

Option A

Option B

I flip a coin.

Heads, you get 1 extra homework point.

Tails, you get 9 extra homework points.

I give you 5 extra homework points.

Heads, you get 5 extra homework points.

Tails, you get 5 extra homework points.

Option A

Option B

I flip a coin.

Heads, you get 1 extra homework point.

Tails, you get 9 extra homework points.

I give you 5 extra homework points.

Heads, you get 5 extra homework points.

Tails, you get 5 extra homework points.

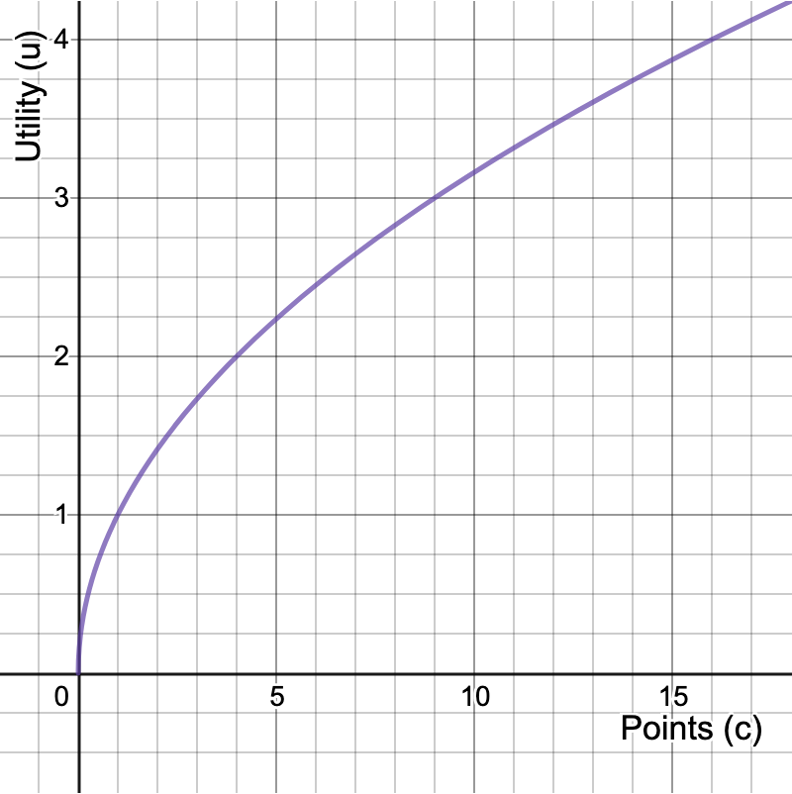
Expected Utility

Suppose your utility from points is given by

v(c) = \sqrt{c}

v(c_1) =

v(c_2) =

\mathbb{E}[c] = {1 \over 2} \times 1 + {1 \over 2} \times 9 =

Expected value of the homework points (c) is:

c_1 = 1

c_2 = 9

\mathbb{E}[c]

c_1

c_2

v(c_1)

v(c_2)

Expected value of your utility (u) is:

\mathbb{E}[v] = {1 \over 2} \times 1 + {1 \over 2} \times 3 =

\mathbb{E}[v]

Risk Aversion

v(c) = \sqrt{c}

\mathbb{E}[c] = {1 \over 2} \times 1 + {1 \over 2} \times 9 =

Expected value of the homework points (c) is:

\mathbb{E}[c]

c_1

c_2

v(c_1)

v(c_2)

v(\mathbb{E}[c])

Utility from expected points is:

v(\mathbb{E}[c]) =

\sqrt{5} \approx 2.25

Expected value of your utility (u) is:

\mathbb{E}[v] = 2

\mathbb{E}[v]

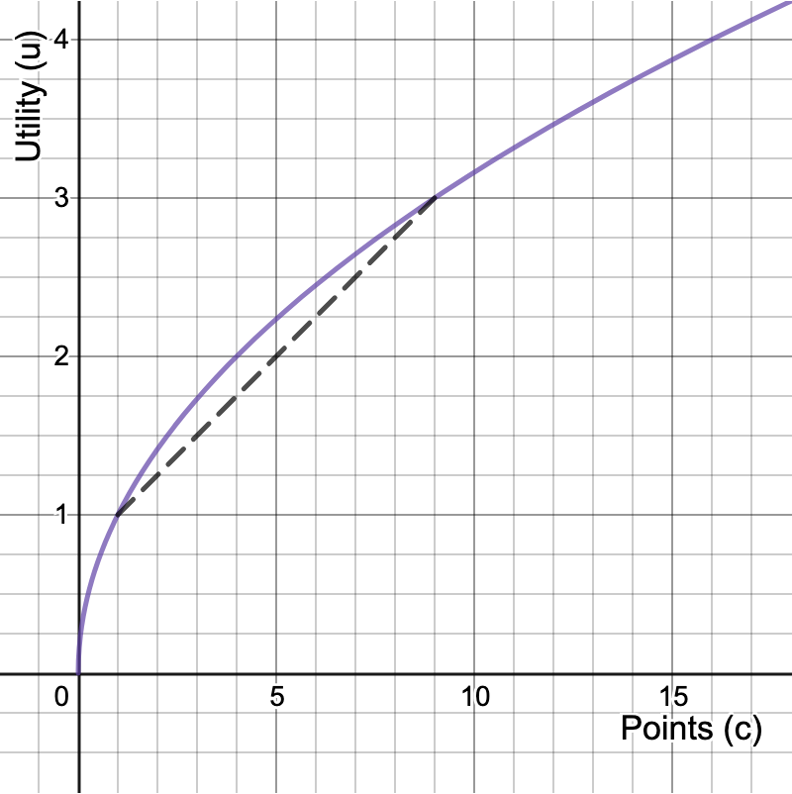
Because the utility from having 5 points for sure is higher than the expected utility of the lottery, this person would be risk averse.

\mathbb{E}[c]

c_1

c_2

v(c_1)

v(c_2)

u(\mathbb{E}[c])

Utility from expected points:

v(\mathbb{E}[c])=\sqrt{5}

Expected utility (u):

\mathbb{E}[v] = 2

\mathbb{E}[v]

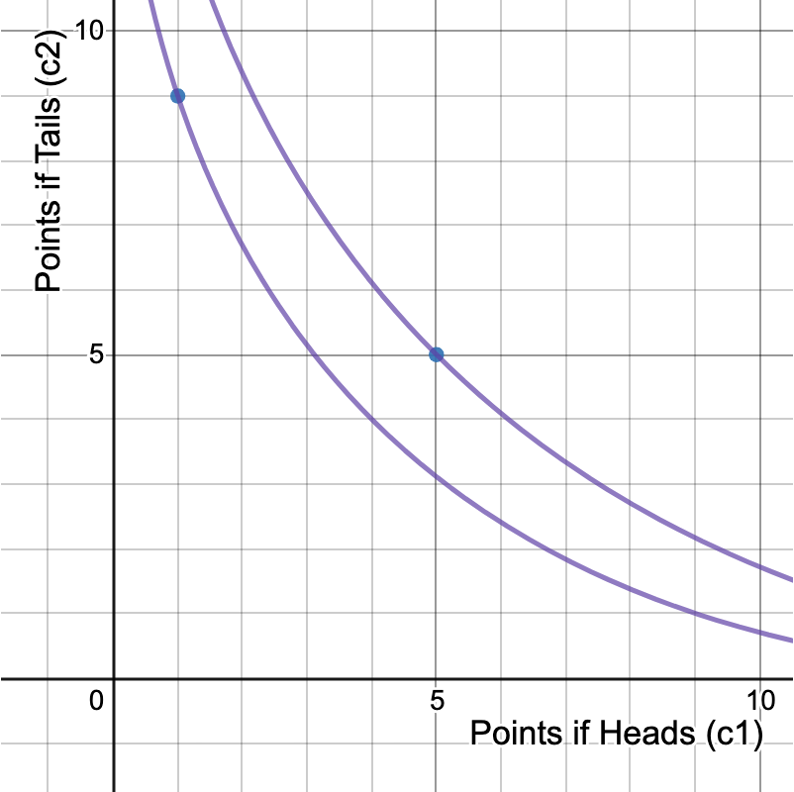
Indifference curve for 2 utils

Indifference curve for

$\sqrt{5}$ utils

\mathbb{E}[c]

c_1

c_2

Option A

Option B

I flip a coin.

Heads, you get 1 extra homework point.

Tails, you get 9 extra homework points.

I give you 4 extra homework points.

Heads, you get 4 extra homework points.

Tails, you get 4 extra homework points.

Is your answer now different than it was before...?

Certainty Equivalent

Suppose your utility from points is given by

v(c) = \sqrt{c}

c_1 = 1

c_2 = 9

\mathbb{E}[c]

c_1

c_2

v(c_1)

v(c_2)

Expected value of your utility (u) is:

\mathbb{E}[v] = {1 \over 2} \times 1 + {1 \over 2} \times 3 =

\mathbb{E}[v]

What amount $CE$, if you had it for sure, would give you the same utility?

v(CE) =2

\mathbb{E}[c]

c_1

c_2

v(c_1)

v(c_2)

\mathbb{E}[v]

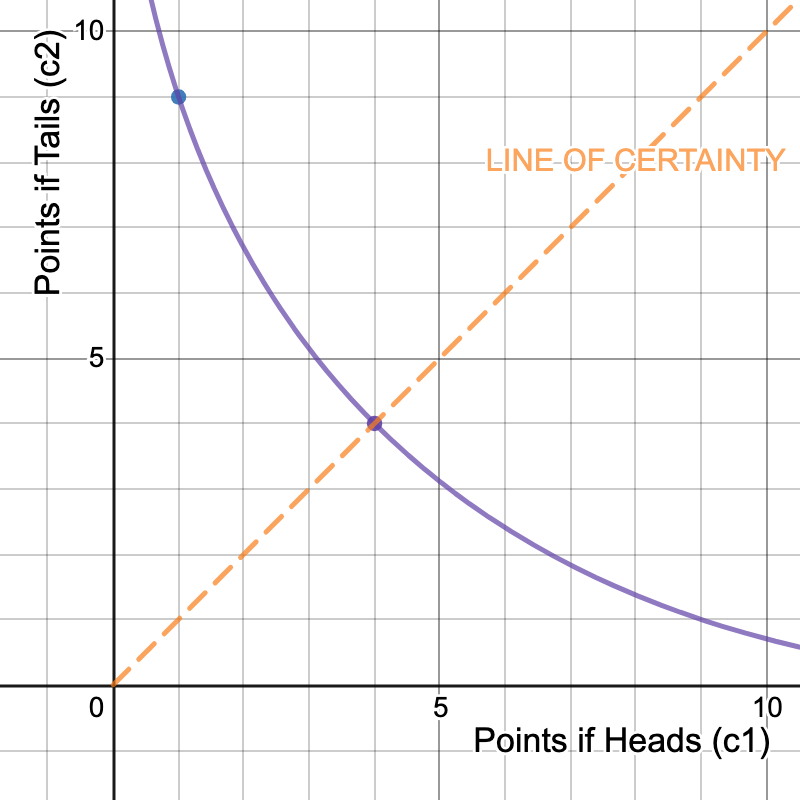
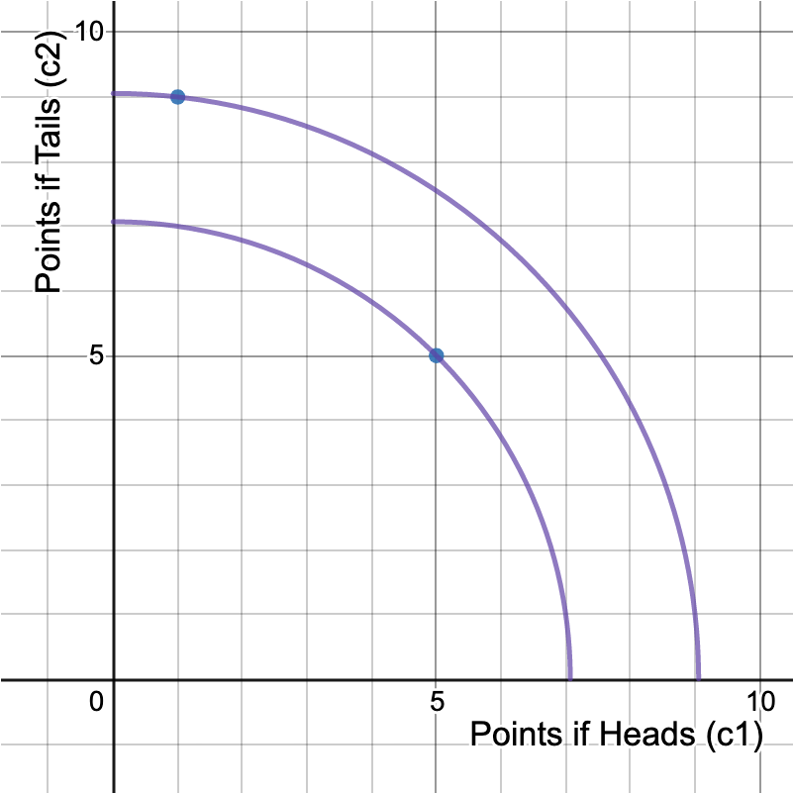
Indifference curve for 2 utils

c_1

c_2

Certainty Equivalent

\mathbb{E}[c]

c_1

c_2

v(c_1)

v(c_2)

\mathbb{E}[v]

Certainty Equivalent = 4

Expected Points = 5

Risk Premium = 1

Risk Premium

How much would you be willing to pay to avoid risk?

What is Sixt offering me here?

Example 1: Betting on a Coin Toss

Example 2: Deal or No Deal

Start with $250 for sure

Would you do it?

If you bet $150 on a coin toss,
you would face the lottery:
50% chance of 100, 50% chance of 400

Two briefcases left: $200K and $1 million

Would you accept that offer? What's the highest offer you would accept?

The "banker" offers you $561,000 to walk away; or you could pick one of the cases.

A lottery is a set of outcomes,
each of which occurs with a known probability.

Lotteries

Example 1: Betting on a Coin Toss

Start with $250 for sure

If you bet $150 on a coin toss,
you would face the lottery:
50% chance of 100,
50% chance of 400

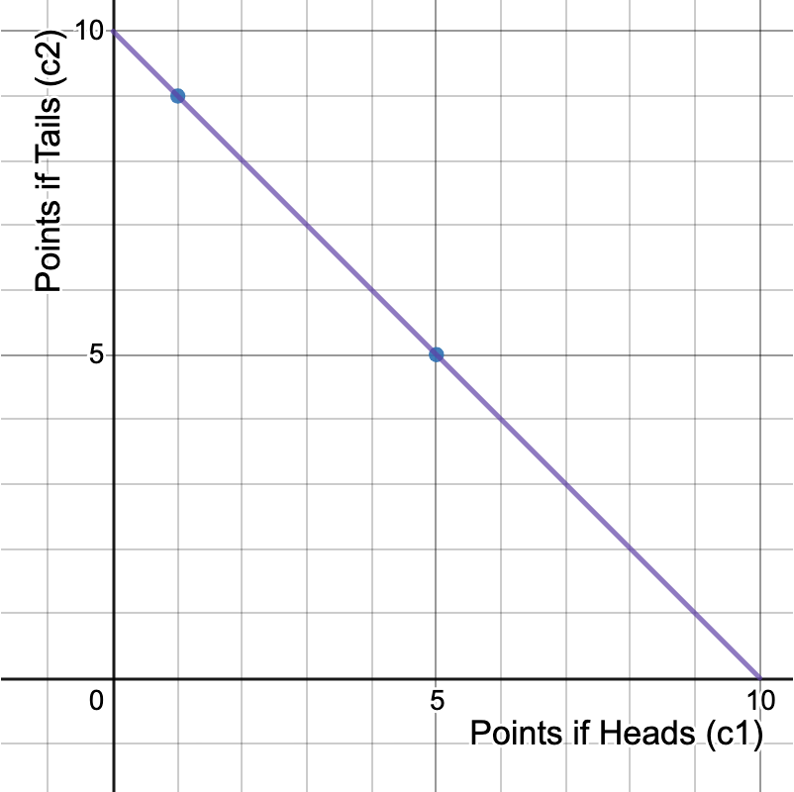
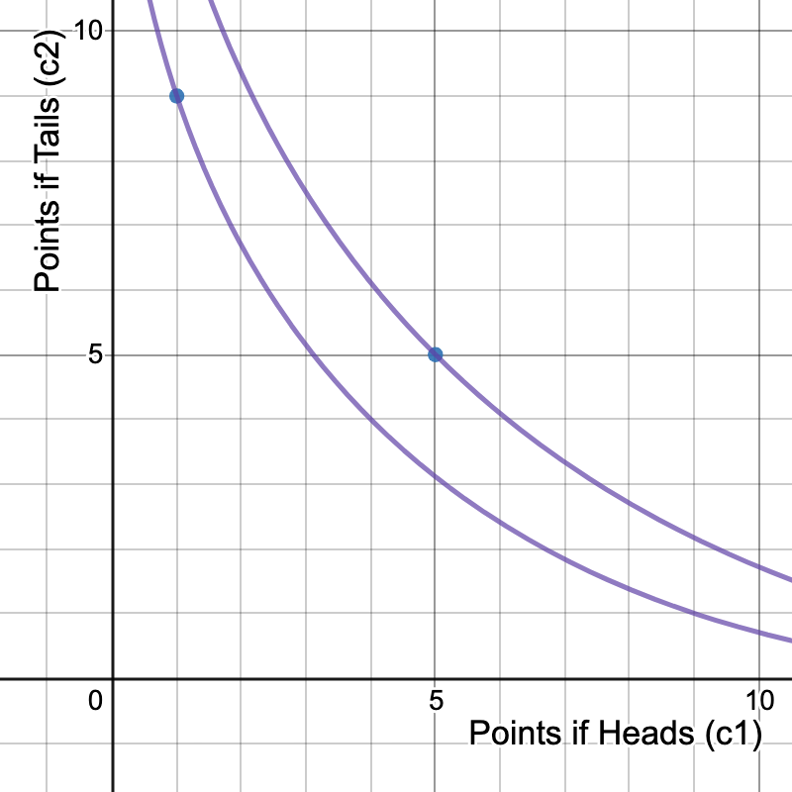
We can represent a lottery as a "bundle" in "state 1 - state 2 space"

Suppose the way you feel about money doesn't depend on the state of the world.

Independence Assumption

Payoff if don't take the bet: $v(250)$

Payoff if win the bet: $v(400)$

Payoff if lose the bet: $v(100)$

\text{Suppose you consume }c_1\text{ with probability }\pi_1

\text{and consume }c_2\text{ with probability }\pi_2

\text{Expected consumption: }\mathbb{E}[c] = \pi_1 c_1 + \pi_2 c_2

\text{Suppose your indirect utility from consuming }c\text{ is }v(c)

\text{Expected utility: }u(c_1,c_2) = \mathbb{E}[v(c)] = \pi_1 v(c_1) + \pi_2 v(c_2)

Expected Utility

"Von Neumann-Morgenstern Utility Function"

Probability-weighted average of a consistent within-state utility function $v(c_s)$

Last time: $c_1$, $c_2$ represented
consumption in different time periods.

This time: $c_1$, $c_2$ represent
consumption in different states of the world.

u(c_1,c_2) = v(c_1)+\beta v(c_2)

u(c_1,c_2) = \pi_1 v(c_1)+ \pi_2 v(c_2)

Comparison to intertemporal consumption

You can combine them! Imagine your consumption next period is $c_2^L$ with probability $\pi$ and $c_2^H$ with probability $1-\pi$:

u(c_1,c_2^L,c_2^H) = v(c_1)+\beta \left[\pi v(c_2^L) + (1-\pi)v(c_2^H)\right]

Marginal Rate of Substitution

u(c_1,c_2) = \pi v(c_1) + (1-\pi) v(c_2)

MRS =

MU_1 = \text{MU from another dollar in state 1} =

MU_2 = \text{MU from another dollar in state 2} =

\pi \times v'(c_1)

(1-\pi) \times v'(c_2)

\text{Expected consumption: }\mathbb{E}[c] = \pi_1 c_1 + \pi_2 c_2

\text{Expected of the lottery: }\mathbb{E}[v(c)] = \pi_1 v(c_1) + \pi_2 v(c_2)

\text{Risk averse: }v(\mathbb{E}[c]) > \mathbb{E}[v(c)]

\text{Risk neutral: }v(\mathbb{E}[c]) = \mathbb{E}[v(c)]

\text{Risk loving: }v(\mathbb{E}[c]) < \mathbb{E}[v(c)]

You prefer having E[c] for sure to taking the gamble

You're indifferent between the two

You prefer taking the gamble to having E[c] for sure

\text{Utility from having }\mathbb{E}[c]\text{ for sure: }v(\mathbb{E}[c]) = v(\pi_1 c_1 + \pi_2 c_2)

Risk Aversion

\text{Risk averse: }v(\mathbb{E}[c]) > \mathbb{E}[v(c)]

You prefer having E[c] for sure to taking the gamble

\text{Risk neutral: }v(\mathbb{E}[c]) = \mathbb{E}[v(c)]

\text{Risk loving: }v(\mathbb{E}[c]) < \mathbb{E}[v(c)]

You're indifferent between the two

You prefer taking the gamble to having E[c] for sure

Certainty Equivalence

"How much money would you need to have for sure

to be just as well off as you are with your current gamble?"

Risk Premium

"How much would you be willing to pay to avoid a fair bet?"